3.3.2抛物线的简单几何性质第2、3课时 课件-2022-2023学年高二上学期数学人教A版（2019）选择性必修第一册(共21张PPT)

(共21张PPT)
第三章 圆锥曲线的方程
3.3.2 抛物线的简单几何性质
3.3 抛物线
抛物线的简单几何性质
标准方程 y2＝2px(p>0) y2＝－2px(p>0) x2＝2py(p>0) x2＝－2py(p>0)
图形
焦点坐标
准线方程
范围 x≥0，y∈R
对称轴 x轴
顶点坐标 O(0,0)
离心率 e＝1
焦半径
通径长 2p
x≤0，y∈R
x轴
O(0,0)
e＝1
2p
y轴
O(0,0)
e＝1
2p
y轴
O(0,0)
e＝1
2p
y≥0，x∈R
y≤0，x∈R
复习巩固
题型二 直线与抛物线的位置关系
典型例题
精讲精练
例3 已知抛物线的方程为 ，直线 的斜率为 ，且过定点 ， 为何值时，直线 与抛物线 只有一个公共点？有两个公共点？没有公共点？
角度1 直线与抛物线的位置关系的判定
[解析] 由题意，知直线 的方程为 ，
由
可得 .①
当 时，由方程①得 ，
把 代入 ，得 ，
此时直线 与抛物线只有一个公共点 .
当 时，方程①的判别式 .
当 时，方程①的判别式 .
由 ，即 ，解得 或 ，所以方程①只有一个解，从而方程组 只有一组解，此时直线 与抛物线只有一个公共点.
由 ，即 ，解得 ，所以当 ，且 时，方程①有两个解，从而方程组 有两组解，此时直线 与抛物线有两个公共点.
由 ，即 ，解得 或 ，所以当 或 时，方程①没有实数解，从而方程组 没有解，直线 与抛物线无公共点.
综上，当 或 或 时，直线 与抛物线只有一个公共点；
当 ，且 时，直线 与抛物线有两个公共点；
当 或 时，直线 与抛物线没有公共点.
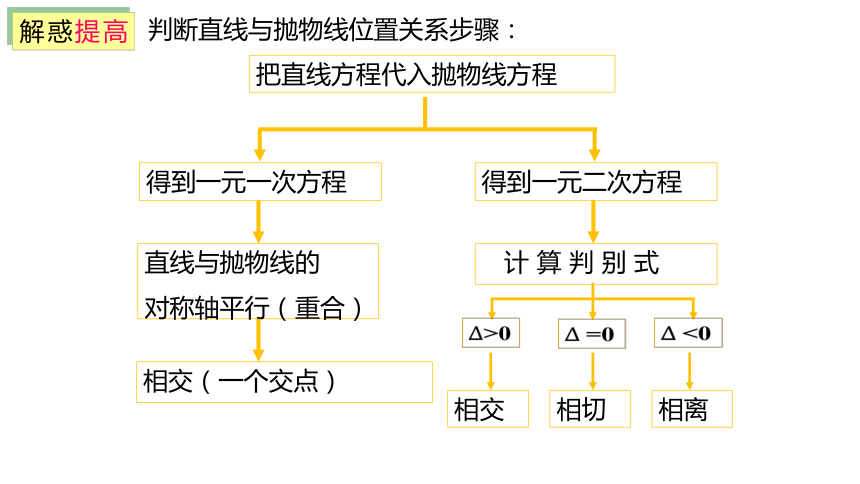
判断直线与抛物线位置关系步骤：
解惑提高
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行（重合）
相交（一个交点）
计 算 判 别 式
>0
=0
<0
相交
相切
相离
巩固训练 已知点 和抛物线 ，求过点 且与抛物线 有且仅有一个公共点的直线 的方程.
[解析] 当直线 的斜率不存在时，由直线 过点 可知，其方程为 ，经验证满足题意.
当直线 的斜率存在时，设直线 的方程为 .
与抛物线 的方程联立得 消去 得， .①
当 时，得 ，可知此时直线 与抛物线相交于点 ，即直线 的方程为 .
当 时，关于 的一元二次方程①的判别式 .
由 得 ，可知此时直线 与抛物线 有且仅有一个公共点，直线 的方程为 ，即 .
综上，直线 的方程为 或 或 .
角度2 焦点弦问题
例4 斜率为的直线经过抛物线 的焦点，与抛物线相交于两点，求焦点弦长的长．
典型例题
例4 斜率为的直线经过抛物线 的焦点，与抛物线相交于两点，求焦点弦长的长．
解：方法二：设A(,), B(,),
直线l的为抛物线方程，得
x2-6x+1=0
∴ +=6, =1
解：方法三(数形结合)：由右图及抛物线的定义可知：
所以
1.过抛物线焦点的直线与抛物线相交，直线被抛物线所截得的线段称为抛物线的焦点弦.四种标准方程形式下的焦点弦长 , 为
标准方程
焦点弦长
2.过抛物线的焦点作垂直于对称轴的直线交抛物线于 , 两点，线段 称为抛物线的通径
通径的长 等于 ，通径是最短的焦点弦长.
解惑提高
变式训练　设点P(x，y)(y≥0)为平面直角坐标系xOy内的一个动点(其中O为坐标原点)，点P到定点M的距离比点P到x轴的距离大.
(1)求点P的轨迹方程；
(2)若直线l：y＝kx＋1与点P的轨迹相交于A，B两点，且|AB|＝ ，求实数k的值.
轨迹方程为x2＝2y.
解　由题意设A(x1，y1)，B(x2，y2)，
∴k4＋3k2－4＝0，
又k2≥0，∴k2＝1，∴k＝±1.
∴x1＋x2＝2k，x1x2＝－2.
例5 已知 < 、 为抛物线 上不同的两点，抛物线 的焦点为 ，线段 恰被 平分. （1） 求抛物线 的方程；（2） 求直线 的方程.
[解析] （1） 由于抛物线的焦点为 ，所以 ，解得 ，所以抛物线 的方程为 .
角度3 与抛物线有关的中点弦问题
（2） 设 ， ，则 ①， ②，且 ， ，
由②-①得 ，
所以 ，
所以直线 的方程为 ，即 .
1.中点弦问题的两种解题策略
（1）点差法：将两个交点的坐标代入抛物线的方程，作差，由 求得斜率，再由点斜式求解；
（2）传统法：设直线方程，并与抛物线的方程联立，消去 （或 ）得关于
（或 ）的一元二次方程，由根与系数的关系，得两根之和即为中点纵（或横）坐标的2倍，从而求斜率.
解惑提高
题型三 直线与抛物线的综合问题
例6.过抛物线焦点的直线与抛物线相交于A、B两点,过点A和抛物线的顶点的直线交抛物线的准线于D，求证：直线DB平行于抛物线的对称轴.
还有其他解法吗？
例7.已知抛物线 过点 . （1）求抛物线的方程；
（2）为坐标原点， ，为抛物线 上异于原点的不同的两点，直线 , 的斜率分别为 , ，若 ，求证：直线过定点.

[解析] 证明：设点 , 的坐标分别为 , ，
所以 , ，所以 ，得 .
①当直线 的斜率不存在时， ，直线 的方程为 .
②当直线 的斜率存在时，设直线 的方程为 ，
由 消去 后整理得 ，可得 ，得 ，
所以直线 的方程为 ，可化为 .
由①②知直线 过定点 .
例8.　如图所示，抛物线关于x轴对称，它的顶点在坐标原点，点均在抛物线上．(1)求抛物线的方程及其准线方程；
(2)当的斜率存在且倾斜角互补时，求证：直线的斜率为定值．

17
方法总结
直线与抛物线有关问题，其方法的核心基本为“设而不求,联立方程组,韦达定理,数形结合辅助，大胆计算分析” 的实践过程.
抛物线中的定点、定值问题，常选择一参数来表示要研究问题中的几何量，通过运算找到定点、定值，说明与参数无关，也常用特值探路法找定点、定值．
巩固训练
过抛物线的顶点O作两条互相垂直的弦交抛物线于A、B两点。
(1)求证:A,B两点的横坐标之积,纵坐标之积分别为定值；
(2)证明：直线AB过定点；
(3)求AB中点M的轨迹方程；
(4)求的面积的最小值.
拓展内容
有关抛物线焦半径和焦点弦的二级结论
已知过抛物线的焦点F的直线交抛物线于两点，焦点弦的倾斜角为.
， ;
+ 为定值 ；
=;
以为直径的圆必与准线相切；
以为直径的圆必与y轴相切；
过焦点弦的端点的切线互相垂直且焦点在准线上.
1.设F为抛物线C：y2＝3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，O为坐标原点，则△OAB的面积为
√
应用举例
2.过抛物线 的焦点作两条互相垂直的弦 和 ，则 的值为( @9@ )
A. B. C. D.
D
√
4.已知抛物线 的焦点为 ，过点 的直线交抛物线于 ， 两点，且 ，则 ( @19@ )
A. B. C. D.
C