初中数学人教版八年级上册11.1.2 三角形的高、中线与角平分线 导学案(含答案)
文档属性
| 名称 | 初中数学人教版八年级上册11.1.2 三角形的高、中线与角平分线 导学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 496.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 09:42:15 | ||
图片预览



文档简介
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
学习目标:1.掌握三角形的高,中线及角平分线的概念.(重点)
2.掌握三角形的高,中线及角平分线的画法.
3.掌握钝角三角形的两短边上高的画法.(难点)
重点:掌握三角形的高,中线及角平分线的概念.
难点:钝角三角形的两短边上高的画法.
自主学习
一、知识链接
1.如图按要求作图:
P A
A B O B
(1)在左图中,过点P作线段AB的垂线PD;作出线段AB的中点E,则有____=_____.
(2)在右图中,作出∠AOB的平分线,则有∠_____=∠_____=____∠AOB.
二、新知预习
1.三角形的高:
(1)小学我们已经学过三角形的高,如图①,过点A向它的对边画垂线,作出△ABC的高AD.
(2)自主归纳:
①从三角形的一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高.
②一个三角形有______条高,请在图①中作出△ABC的另外两条高.
③三角形的高是一条_______.
2.(1)如图②,连接△ABC的顶点A和它的边BC的中点D,类比三角形高线的定义,则所得的线段AD叫做△ABC的边BC上的_____线,画出△ABC其他的两条中线.
(2)自主归纳:
①在三角形中,连接一个顶点与它对边的中点的线段,叫做这个三角形的中线.
②一个三角形有_____条中线,每条中线都是一条______.
3.三角形的角平分线:
(1)如图③,你能用同样的方法画出任意一个三角形的一个内角的平分线吗
(2)自主归纳
①三角形角平分线定义:________________________.
②三角形的角平分线与角的平分线的区别是:______________.
③一个三角形有_______条角平分线.
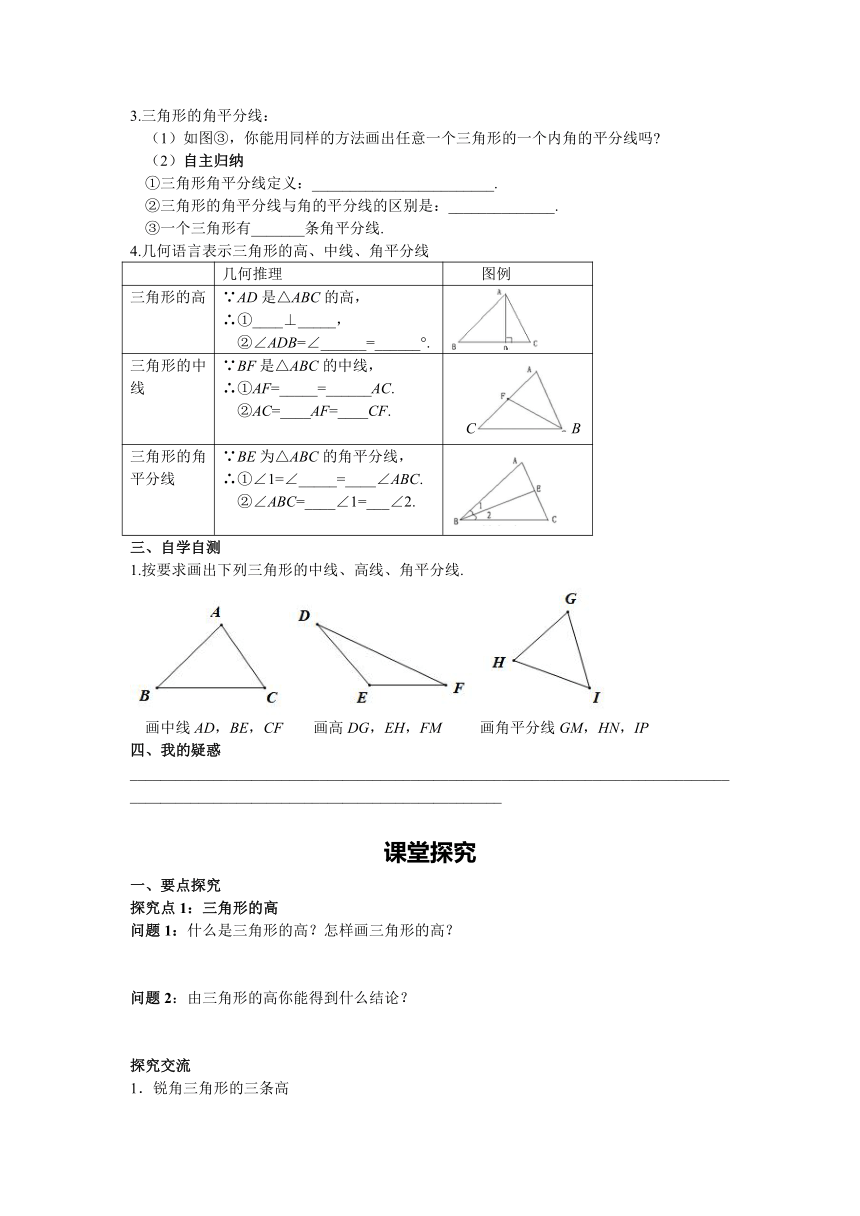
4.几何语言表示三角形的高、中线、角平分线
几何推理 图例
三角形的高 ∵AD是△ABC的高, ∴①____⊥_____, ②∠ADB=∠______=______°.
三角形的中线 ∵BF是△ABC的中线, ∴①AF=_____=______AC. ②AC=____AF=____CF. CB
三角形的角平分线 ∵BE为△ABC的角平分线, ∴①∠1=∠_____=____∠ABC. ②∠ABC=____∠1=___∠2.
三、自学自测
1.按要求画出下列三角形的中线、高线、角平分线.
画中线AD,BE,CF 画高DG,EH,FM 画角平分线GM,HN,IP
四、我的疑惑
________________________________________________________________________________________________________________________________
课堂探究
要点探究
探究点1:三角形的高
问题1:什么是三角形的高?怎样画三角形的高?
问题2:由三角形的高你能得到什么结论?
探究交流
1.锐角三角形的三条高
(1)你能画出这个三角形的三条高吗?
(2)这三条高之间有怎样的位置关系?
(3)锐角三角形的三条高是在三角形的内部还是外部?
2.直角三角形的三条高
(1)画出直角三角形的三条高.
(2)它们有怎样的位置关系?
直角边BC上的高是 ;直角边AB上的高是 ;斜边AC上的高是 .
3.钝角三角形的三条高
(1)钝角三角形的三条高相交吗?
(2)AC边上的高是哪条线段?AB边上的高是哪条线段?BC边上的高是哪条线段?
(3)钝角三角形的三条高交于一点吗?
(4)它们所在的直线交于一点吗?这点位于何处?
归纳 三角形的三条高的特性
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
典例精析
例1 如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,求BP的最小值.
方法总结:面积法的应用:若涉及两条高求长度,一般需结合面积(但不求出面积),利用三角形面积的两种不同表示方法列等式求解.
探究点2:三角形的中线
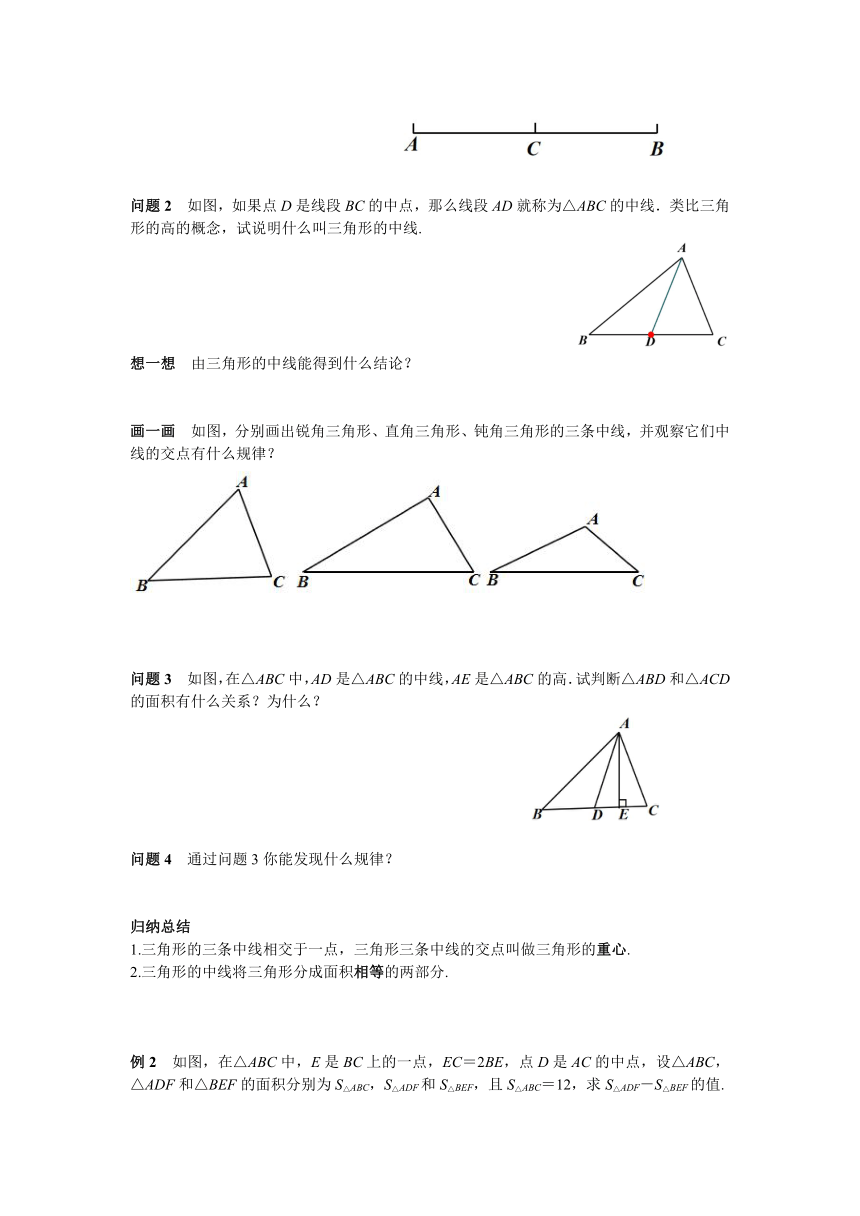
问题1 如图,如果点C是线段AB的中点,你能得到什么结论?
问题2 如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线.
想一想 由三角形的中线能得到什么结论?
画一画 如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
问题3 如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?
问题4 通过问题3你能发现什么规律?
归纳总结
1.三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
2.三角形的中线将三角形分成面积相等的两部分.
例2 如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
探究点3:三角形的角平分线
问题1 如图,若OC是∠AOB的平分线,你能得到什么结论?
问题2 你能用同样的方法画出任意一个三角形的一个内角的平分线吗
问题3 一个三角形有几条角平分线?
问题4 请画出这个三角形的另外两条角平分线,你发现了什么?
例3 如图,DC平分∠ACB,DE∥BC,∠AED=80°,求∠ECD的度数.
二、课堂小结
三角形的高:从三角形的一个顶点向它的对边作垂线,顶点和垂足之间
的线段.
三角形的中线:在三角形中,连接一个顶点和它对边中点的线段,三角
形的中线把三角形分为面积相等的两个三角形.
三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,
连接这个角的顶点与交点的线段.
当堂检测
1.下列说法正确的是 ( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是 ( )
A.①② B.③④ C.①④ D.②③
3.如图,△ABC中∠ACB=90°,CD⊥AB,图中线段中可以作为△ABC的高的有 ( )
A.2条 B.3条 C.4条 D.5条
4.下列各组图形,哪一组图形中AD是△ABC 的BC边上的高 ( )
5.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则 AB= 2 ,BD= ,AE= .
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=_______,∠3=________,
∠ABC=2______.
6.如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,则S△ABC=____.
7.在△ABC中,CD是中线,已知BC-AC=5 cm,△DBC的周长为25 cm,求△ADC的周长.
能力提升
王大爷有一块三角形的菜地,现在要将它们平均分给四个儿子,在菜地的一角A处有一口池塘,为了使分开后的四块菜地都就近取水,王大爷为此很伤脑筋.你能想出什么办法帮帮王大爷吗?
如果不考虑水源,你认为还可以怎样分
参考答案
自主学习
一、知识链接
1.解:(1)AE BE 如图,线段PD,点E即为所求.
(2)AOC BOC 如图,射线OC即为所求.
二、新知预习
1.解:(1)如图①(1),线段AD即为所求.
(2)②3 如图①(2),线段BE、CF即为所求.
③线段
2.解:(1)中 如图②,线段BE、CF即为所求.
(2)②3 线段
3.解:(1)如图③,线段AD即为所求.
(2)①三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段
②三角形的角平分线是一条线段,角的平分线是一条射线 ③3
4.三角形的高:AD BC ADC 90
三角形的中线:CF 2 2
三角形的角平分线:2 2 2
三、自学自测
1.如图所示即为所求.
四、我的疑惑
课堂探究
一、要点探究
探究点1:三角形的高
问题1 解:定义 如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
问题2 解:∠ADB= ∠ADC=90 °.
探究交流
1.锐角三角形的三条高
问题1 解:(1)如图所示.
(2)锐角三角形的三条高交于同一点.
(3) 锐角三角形的三条高都在三角形的内部.
2.直角三角形的三条高
(1)如图所示.
(2) BD AB BC 直角三角形的三条高交于直角顶点.
3.钝角三角形的三条高
(1)如图所示.
(2)BF CE AD
(3)钝角三角形的三条高不相交于一点.
(4)钝角三角形的三条高所在直线交于一点.并且这个点在三角形外部.
归纳 3 1 1 相交 相交 不相交 相交 相交 相交 三角形内部 直角顶点 三角形外部
典例精析
例1 解:根据垂线段最短,可知当BP⊥AC时,BP有最小值.
由△ABC的面积公式可知,AD·BC=BP·AC.
代入数值,可解得BP=.
探究点2:三角形的中线
问题1 解:AC=BC=AB.
问题2 解: 定义:如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
想一想 解:BD=CD=BC.
画一画 解:如图,三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.
问题3 解:相等,因为两个三角形等底同高,所以它们面积相等.
问题4 解:三角形的中线能将三角形的面积平分.
例2 解:∵点D是AC的中点,∴AD=AC.
∵S△ABC=12,∴S△ABD=S△ABC=×12=6.
∵EC=2BE,S△ABC=12,∴S△ABE=S△ABC=×12=4.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
∴S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
探究点3:三角形的角平分线
问题1 解:∠AOC= ∠BOC.
问题2 解:如图.
想一想 解:相同点是:∠ABD=∠CBD;不同点是:前者是线段,后者是射线.
问题3 解:3条角平分线
问题4 解,如图,三角形的三条角平分线交于一点,称之为三角形的内心.
例3 解:∵DC平分∠ACB,∴∠ECD=∠BCD=∠ACB.
又DE∥BC,∴∠ACB=∠AED=80°.∴∠ECD=40°.
当堂检测
1.B 2.D 3.B 4.D
5.(1)AF DC AC
(2)∠CAD ∠BCF ∠2
6.12
7.解:∵CD是△ABC的中线,∴BD=AD .
∵BC-AC=5 cm,∴△DBC与△ADC的周长差是5 cm.
又∵△DBC的周长为25 cm,
∴△ADC的周长为25-5=20(cm).
能力提升
思路提示:想到三角形的中线能把三角形分成面积相等的两部分.
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
学习目标:1.掌握三角形的高,中线及角平分线的概念.(重点)
2.掌握三角形的高,中线及角平分线的画法.
3.掌握钝角三角形的两短边上高的画法.(难点)
重点:掌握三角形的高,中线及角平分线的概念.
难点:钝角三角形的两短边上高的画法.
自主学习
一、知识链接
1.如图按要求作图:
P A
A B O B
(1)在左图中,过点P作线段AB的垂线PD;作出线段AB的中点E,则有____=_____.
(2)在右图中,作出∠AOB的平分线,则有∠_____=∠_____=____∠AOB.
二、新知预习
1.三角形的高:
(1)小学我们已经学过三角形的高,如图①,过点A向它的对边画垂线,作出△ABC的高AD.
(2)自主归纳:
①从三角形的一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高.
②一个三角形有______条高,请在图①中作出△ABC的另外两条高.
③三角形的高是一条_______.
2.(1)如图②,连接△ABC的顶点A和它的边BC的中点D,类比三角形高线的定义,则所得的线段AD叫做△ABC的边BC上的_____线,画出△ABC其他的两条中线.
(2)自主归纳:
①在三角形中,连接一个顶点与它对边的中点的线段,叫做这个三角形的中线.
②一个三角形有_____条中线,每条中线都是一条______.
3.三角形的角平分线:
(1)如图③,你能用同样的方法画出任意一个三角形的一个内角的平分线吗
(2)自主归纳
①三角形角平分线定义:________________________.
②三角形的角平分线与角的平分线的区别是:______________.
③一个三角形有_______条角平分线.
4.几何语言表示三角形的高、中线、角平分线
几何推理 图例
三角形的高 ∵AD是△ABC的高, ∴①____⊥_____, ②∠ADB=∠______=______°.
三角形的中线 ∵BF是△ABC的中线, ∴①AF=_____=______AC. ②AC=____AF=____CF. CB
三角形的角平分线 ∵BE为△ABC的角平分线, ∴①∠1=∠_____=____∠ABC. ②∠ABC=____∠1=___∠2.
三、自学自测
1.按要求画出下列三角形的中线、高线、角平分线.
画中线AD,BE,CF 画高DG,EH,FM 画角平分线GM,HN,IP
四、我的疑惑
________________________________________________________________________________________________________________________________
课堂探究
要点探究
探究点1:三角形的高
问题1:什么是三角形的高?怎样画三角形的高?
问题2:由三角形的高你能得到什么结论?
探究交流
1.锐角三角形的三条高
(1)你能画出这个三角形的三条高吗?
(2)这三条高之间有怎样的位置关系?
(3)锐角三角形的三条高是在三角形的内部还是外部?
2.直角三角形的三条高
(1)画出直角三角形的三条高.
(2)它们有怎样的位置关系?
直角边BC上的高是 ;直角边AB上的高是 ;斜边AC上的高是 .
3.钝角三角形的三条高
(1)钝角三角形的三条高相交吗?
(2)AC边上的高是哪条线段?AB边上的高是哪条线段?BC边上的高是哪条线段?
(3)钝角三角形的三条高交于一点吗?
(4)它们所在的直线交于一点吗?这点位于何处?
归纳 三角形的三条高的特性
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
典例精析
例1 如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,求BP的最小值.
方法总结:面积法的应用:若涉及两条高求长度,一般需结合面积(但不求出面积),利用三角形面积的两种不同表示方法列等式求解.
探究点2:三角形的中线
问题1 如图,如果点C是线段AB的中点,你能得到什么结论?
问题2 如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线.
想一想 由三角形的中线能得到什么结论?
画一画 如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
问题3 如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?
问题4 通过问题3你能发现什么规律?
归纳总结
1.三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
2.三角形的中线将三角形分成面积相等的两部分.
例2 如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
探究点3:三角形的角平分线
问题1 如图,若OC是∠AOB的平分线,你能得到什么结论?
问题2 你能用同样的方法画出任意一个三角形的一个内角的平分线吗
问题3 一个三角形有几条角平分线?
问题4 请画出这个三角形的另外两条角平分线,你发现了什么?
例3 如图,DC平分∠ACB,DE∥BC,∠AED=80°,求∠ECD的度数.
二、课堂小结
三角形的高:从三角形的一个顶点向它的对边作垂线,顶点和垂足之间
的线段.
三角形的中线:在三角形中,连接一个顶点和它对边中点的线段,三角
形的中线把三角形分为面积相等的两个三角形.
三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,
连接这个角的顶点与交点的线段.
当堂检测
1.下列说法正确的是 ( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是 ( )
A.①② B.③④ C.①④ D.②③
3.如图,△ABC中∠ACB=90°,CD⊥AB,图中线段中可以作为△ABC的高的有 ( )
A.2条 B.3条 C.4条 D.5条
4.下列各组图形,哪一组图形中AD是△ABC 的BC边上的高 ( )
5.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则 AB= 2 ,BD= ,AE= .
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=_______,∠3=________,
∠ABC=2______.
6.如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,则S△ABC=____.
7.在△ABC中,CD是中线,已知BC-AC=5 cm,△DBC的周长为25 cm,求△ADC的周长.
能力提升
王大爷有一块三角形的菜地,现在要将它们平均分给四个儿子,在菜地的一角A处有一口池塘,为了使分开后的四块菜地都就近取水,王大爷为此很伤脑筋.你能想出什么办法帮帮王大爷吗?
如果不考虑水源,你认为还可以怎样分
参考答案
自主学习
一、知识链接
1.解:(1)AE BE 如图,线段PD,点E即为所求.
(2)AOC BOC 如图,射线OC即为所求.
二、新知预习
1.解:(1)如图①(1),线段AD即为所求.
(2)②3 如图①(2),线段BE、CF即为所求.
③线段
2.解:(1)中 如图②,线段BE、CF即为所求.
(2)②3 线段
3.解:(1)如图③,线段AD即为所求.
(2)①三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段
②三角形的角平分线是一条线段,角的平分线是一条射线 ③3
4.三角形的高:AD BC ADC 90
三角形的中线:CF 2 2
三角形的角平分线:2 2 2
三、自学自测
1.如图所示即为所求.
四、我的疑惑
课堂探究
一、要点探究
探究点1:三角形的高
问题1 解:定义 如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
问题2 解:∠ADB= ∠ADC=90 °.
探究交流
1.锐角三角形的三条高
问题1 解:(1)如图所示.
(2)锐角三角形的三条高交于同一点.
(3) 锐角三角形的三条高都在三角形的内部.
2.直角三角形的三条高
(1)如图所示.
(2) BD AB BC 直角三角形的三条高交于直角顶点.
3.钝角三角形的三条高
(1)如图所示.
(2)BF CE AD
(3)钝角三角形的三条高不相交于一点.
(4)钝角三角形的三条高所在直线交于一点.并且这个点在三角形外部.
归纳 3 1 1 相交 相交 不相交 相交 相交 相交 三角形内部 直角顶点 三角形外部
典例精析
例1 解:根据垂线段最短,可知当BP⊥AC时,BP有最小值.
由△ABC的面积公式可知,AD·BC=BP·AC.
代入数值,可解得BP=.
探究点2:三角形的中线
问题1 解:AC=BC=AB.
问题2 解: 定义:如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
想一想 解:BD=CD=BC.
画一画 解:如图,三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.
问题3 解:相等,因为两个三角形等底同高,所以它们面积相等.
问题4 解:三角形的中线能将三角形的面积平分.
例2 解:∵点D是AC的中点,∴AD=AC.
∵S△ABC=12,∴S△ABD=S△ABC=×12=6.
∵EC=2BE,S△ABC=12,∴S△ABE=S△ABC=×12=4.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
∴S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
探究点3:三角形的角平分线
问题1 解:∠AOC= ∠BOC.
问题2 解:如图.
想一想 解:相同点是:∠ABD=∠CBD;不同点是:前者是线段,后者是射线.
问题3 解:3条角平分线
问题4 解,如图,三角形的三条角平分线交于一点,称之为三角形的内心.
例3 解:∵DC平分∠ACB,∴∠ECD=∠BCD=∠ACB.
又DE∥BC,∴∠ACB=∠AED=80°.∴∠ECD=40°.
当堂检测
1.B 2.D 3.B 4.D
5.(1)AF DC AC
(2)∠CAD ∠BCF ∠2
6.12
7.解:∵CD是△ABC的中线,∴BD=AD .
∵BC-AC=5 cm,∴△DBC与△ADC的周长差是5 cm.
又∵△DBC的周长为25 cm,
∴△ADC的周长为25-5=20(cm).
能力提升
思路提示:想到三角形的中线能把三角形分成面积相等的两部分.
