高一数学 1.2.2 函数的表示法 第二课时课件 新人教A版必修1
文档属性
| 名称 | 高一数学 1.2.2 函数的表示法 第二课时课件 新人教A版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 464.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 14:24:33 | ||
图片预览











文档简介
课件33张PPT。1.2.2 函数的表示法(二)1.了解分段函数的概念,会画分段函数的图象,并能解决相关问题.
2.了解映射的概念及含义,会判断给定的对应关系是否是映射.1.了解分段函数的概念,会画分段函数的图象,并能解决相关问题.
2.了解映射的概念及含义,会判断给定的对应关系是否是映射.
课前自主学习1.分段函数
(1)分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的_________的函数.
(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的_____;各段函数的定义域的交集是空集.
(3)作分段函数图象时,应_________________ _____ .
?
自学导引对应关系并集分别作出每一段的图象2.映射的概念
设A、B是两个非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中_________确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的_________ .
都有唯一一个映射函数与映射的主要联系和区别是什么?
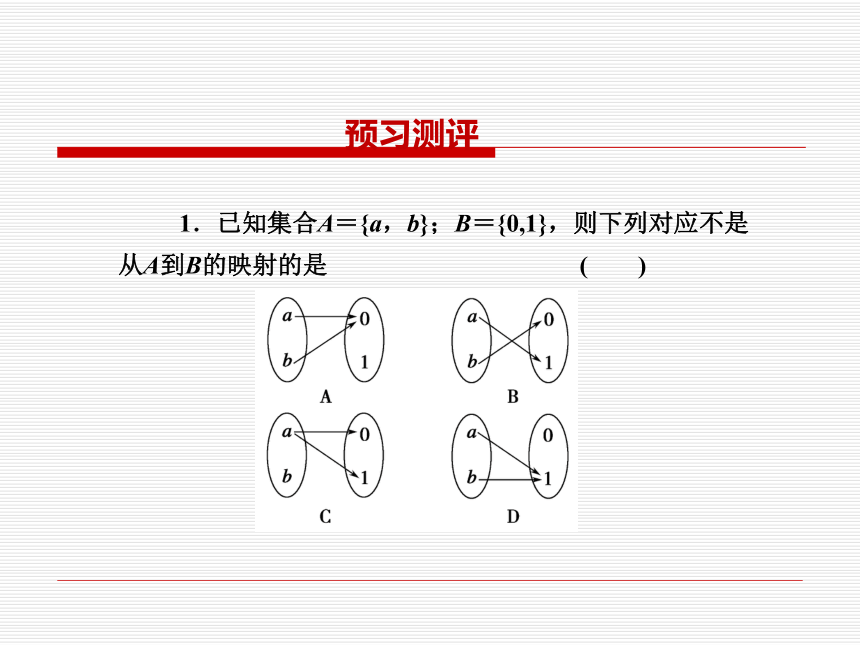
答:函数是一个特殊的映射,函数是非空数集A到非空数集B的映射;而对于映射而言,A和B不一定是数集.自主探究1.已知集合A={a,b};B={0,1},则下列对应不是从A到B的映射的是 ( )
预习测评解析:A、B、D均满足映射定义,C不满足集合A中任一元素在集合B中有唯一元素与之对应,且集合A中元素b在集合B中无唯一元素与之对应.
答案:C答案:A答案:(-∞,0)∪(0,+∞)
4.已知A=R,B=[1,+∞),对应关系f:x→x2+1,则A中元素1对应于B中的元素________,A中元素-1对应于B中的元素________,A中的元素________对应于B中元素1.
解析:x=1时,x2+1=12+1=2;x=-1时,x2+1=(-1)2+1=2;x2+1=1时,解得x=0.
答案:2 2 0 课堂讲练互动1.分段函数
(1)有些函数在它的定义域中,对于自变量x的不同取值区间,对应关系也不同,这样的函数通常称为分段函数,分段函数是一个函数,而不是几个函数,其解析式是由几个不同的式子构成的,它们合为一个整体表示一个函数.
(2)画分段函数的图象时,一定要考虑区间端点是否包含在内,若端点包含在内,则用实点“·”表示,若端点不包含在内,则用虚点 “。” 表示.要点阐释(3)写分段函数定义域时,区间端点应不重不漏.
(4)处理分段函数问题时,要首先确定自变量的取值属于哪一个范围,然后选取相应的对应关系.
(5)求分段函数的定义域则是各段定义域的并集;求分段函数的值域也是分别求出各段上的值域后取并集;求分段函数最大(小)值则是分别在每段上求出最大(小)值,然后取各段中的最大(小)值.
2.映射
(1)映射f:A→B是由非空集合A、B以及A到B的对应关系f所确定的.
(2)映射定义中的两个集合A、B是非空的,可以是数集,也可以是点集或其他集合,A、B是有先后次序的,A到B的映射与B到A的映射一般是截然不同的,即f具有方向性.
(3)映射f:A→B要求:对于集合A中的任何一个元素在集合B中都有唯一的元素和它对应,这样有:
①A中每一个元素都可以在B中找到一个且只有一个元素和它对应.
②A中的不同元素允许对应B中的相同元素,即映射允许“多对一”“一对一”,但不允许“一对多”.
③B中的元素允许A中无元素与之对应.题型一 分段函数的图象
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出该函数的值域.
典例剖析(2)函数f(x)的图象如图所示.(3)由(2)知,f(x)在(-2,2]上的值域为[1,3).点评:1.对含有绝对值的函数,要作出其图象,首先应根据绝对值的意义脱去绝对值符号,将函数转化为分段函数,然后分段作出函数图象.
2.由于分段函数在定义域的不同区间内解析式不一样,因此画图时要特别注意区间端点处对应点的实虚之分.当x≥1时,图象为直线y=x的一部分.
如图所示,由此可知,值域y∈[1,+∞).题型二 分段函数求值
点评:(1)给定自变量求函数值时,应根据自变量所在的范围,利用相应的解析式直接求值;
(2)若给函数值求自变量,应根据每一段的解析式分别求解,但应注意要检验求得的值是否在相应的自变量取值范围内.
题型三 映射概念及应用
【例3】 判断下列对应是不是从集合A到集合B的映射:
(1)A=N*,B=N*,对应关系f:x→|x-3|;
(2)A={平面内的圆},B={平面内的矩形},对应关系f“作圆的内接矩形”;
(3)A={高一·一班的男生},B={男生的身高},对应关系f:每个男生对应自己的身高;
解:(1)由于A中元素3在对应关系f作用下其与3的差的绝对值为0,而0?B,故不是映射.
(2)因为一个圆有无数个内接矩形,即集合A中任何一个元素在集合B中有无数个元素与之对应,故不是映射.
(3)对A中任何一个元素,按照对应关系f,在B中都有唯一一个元素与之对应,符合映射定义,是映射.
点评:给定两集合A,B及对应关系f,判断是否是从集合A到集合B的映射,主要利用映射的定义,用通俗的语言讲:A→B的对应有“多对一”、“一对一”、“一对多”,前两种对应是A到B的映射,而最后一种不是A到B的映射.
3.判断下列对应关系哪些是从集合A到集合B的映射,哪些不是,为什么?(3)设A={矩形},B={实数},对应关系f:矩形和它的面积对应.
解:(1)对于集合A中任意一个非负数在集合B中都有唯一元素1与之对应,对于A中任意一个负数在集合B中都有唯一元素0与之对应,所以这个对应是映射.
(2)集合A中的元素0在集合B中没有元素与之对应,故不是映射.
(3)对于每一个矩形,它的面积是唯一确定的,所以f是从集合A到集合B的映射.误区解密 因忽视分段函数自变量的范围而出错
错解:由x2-1=3得x=±2;
由2x+1=3,得x=1,故x的值为2,-2或1.
错因分析:本题是一个分段函数问题,在解决此类问题时,要紧扣“分段”的特征,即函数在定义域的不同部分,有不同的对应关系,它不是几个函数,而是一个函数,求值时不能忽视x的取值范围.正解:当x≥0时,由x2-1=3,得x=2或x=-2(舍去);当x<0时,由2x+1=3,得x=1 (舍去),故x=2.
纠错心得:对于分段函数分为几部分应看成一个整体才有意义,它的定义域应是各部分x范围的并集,求某个自变量的函数值,容易不看自变量的范围直接代入解析式而求错解.1.分段函数求值要先找准自变量所在的区间;分段函数的定义域、值域分别是各段函数的定义域、值域的并集.
2.判断一个对应是不是映射,先看第一集合A:看集合A中的每一个元素是否都有对应元素,若有,再看对应元素是否唯一;至于集合B中的元素不作任何要求.课堂总结
2.了解映射的概念及含义,会判断给定的对应关系是否是映射.1.了解分段函数的概念,会画分段函数的图象,并能解决相关问题.
2.了解映射的概念及含义,会判断给定的对应关系是否是映射.
课前自主学习1.分段函数
(1)分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的_________的函数.
(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的_____;各段函数的定义域的交集是空集.
(3)作分段函数图象时,应_________________ _____ .
?
自学导引对应关系并集分别作出每一段的图象2.映射的概念
设A、B是两个非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中_________确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的_________ .
都有唯一一个映射函数与映射的主要联系和区别是什么?
答:函数是一个特殊的映射,函数是非空数集A到非空数集B的映射;而对于映射而言,A和B不一定是数集.自主探究1.已知集合A={a,b};B={0,1},则下列对应不是从A到B的映射的是 ( )
预习测评解析:A、B、D均满足映射定义,C不满足集合A中任一元素在集合B中有唯一元素与之对应,且集合A中元素b在集合B中无唯一元素与之对应.
答案:C答案:A答案:(-∞,0)∪(0,+∞)
4.已知A=R,B=[1,+∞),对应关系f:x→x2+1,则A中元素1对应于B中的元素________,A中元素-1对应于B中的元素________,A中的元素________对应于B中元素1.
解析:x=1时,x2+1=12+1=2;x=-1时,x2+1=(-1)2+1=2;x2+1=1时,解得x=0.
答案:2 2 0 课堂讲练互动1.分段函数
(1)有些函数在它的定义域中,对于自变量x的不同取值区间,对应关系也不同,这样的函数通常称为分段函数,分段函数是一个函数,而不是几个函数,其解析式是由几个不同的式子构成的,它们合为一个整体表示一个函数.
(2)画分段函数的图象时,一定要考虑区间端点是否包含在内,若端点包含在内,则用实点“·”表示,若端点不包含在内,则用虚点 “。” 表示.要点阐释(3)写分段函数定义域时,区间端点应不重不漏.
(4)处理分段函数问题时,要首先确定自变量的取值属于哪一个范围,然后选取相应的对应关系.
(5)求分段函数的定义域则是各段定义域的并集;求分段函数的值域也是分别求出各段上的值域后取并集;求分段函数最大(小)值则是分别在每段上求出最大(小)值,然后取各段中的最大(小)值.
2.映射
(1)映射f:A→B是由非空集合A、B以及A到B的对应关系f所确定的.
(2)映射定义中的两个集合A、B是非空的,可以是数集,也可以是点集或其他集合,A、B是有先后次序的,A到B的映射与B到A的映射一般是截然不同的,即f具有方向性.
(3)映射f:A→B要求:对于集合A中的任何一个元素在集合B中都有唯一的元素和它对应,这样有:
①A中每一个元素都可以在B中找到一个且只有一个元素和它对应.
②A中的不同元素允许对应B中的相同元素,即映射允许“多对一”“一对一”,但不允许“一对多”.
③B中的元素允许A中无元素与之对应.题型一 分段函数的图象
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出该函数的值域.
典例剖析(2)函数f(x)的图象如图所示.(3)由(2)知,f(x)在(-2,2]上的值域为[1,3).点评:1.对含有绝对值的函数,要作出其图象,首先应根据绝对值的意义脱去绝对值符号,将函数转化为分段函数,然后分段作出函数图象.
2.由于分段函数在定义域的不同区间内解析式不一样,因此画图时要特别注意区间端点处对应点的实虚之分.当x≥1时,图象为直线y=x的一部分.
如图所示,由此可知,值域y∈[1,+∞).题型二 分段函数求值
点评:(1)给定自变量求函数值时,应根据自变量所在的范围,利用相应的解析式直接求值;
(2)若给函数值求自变量,应根据每一段的解析式分别求解,但应注意要检验求得的值是否在相应的自变量取值范围内.
题型三 映射概念及应用
【例3】 判断下列对应是不是从集合A到集合B的映射:
(1)A=N*,B=N*,对应关系f:x→|x-3|;
(2)A={平面内的圆},B={平面内的矩形},对应关系f“作圆的内接矩形”;
(3)A={高一·一班的男生},B={男生的身高},对应关系f:每个男生对应自己的身高;
解:(1)由于A中元素3在对应关系f作用下其与3的差的绝对值为0,而0?B,故不是映射.
(2)因为一个圆有无数个内接矩形,即集合A中任何一个元素在集合B中有无数个元素与之对应,故不是映射.
(3)对A中任何一个元素,按照对应关系f,在B中都有唯一一个元素与之对应,符合映射定义,是映射.
点评:给定两集合A,B及对应关系f,判断是否是从集合A到集合B的映射,主要利用映射的定义,用通俗的语言讲:A→B的对应有“多对一”、“一对一”、“一对多”,前两种对应是A到B的映射,而最后一种不是A到B的映射.
3.判断下列对应关系哪些是从集合A到集合B的映射,哪些不是,为什么?(3)设A={矩形},B={实数},对应关系f:矩形和它的面积对应.
解:(1)对于集合A中任意一个非负数在集合B中都有唯一元素1与之对应,对于A中任意一个负数在集合B中都有唯一元素0与之对应,所以这个对应是映射.
(2)集合A中的元素0在集合B中没有元素与之对应,故不是映射.
(3)对于每一个矩形,它的面积是唯一确定的,所以f是从集合A到集合B的映射.误区解密 因忽视分段函数自变量的范围而出错
错解:由x2-1=3得x=±2;
由2x+1=3,得x=1,故x的值为2,-2或1.
错因分析:本题是一个分段函数问题,在解决此类问题时,要紧扣“分段”的特征,即函数在定义域的不同部分,有不同的对应关系,它不是几个函数,而是一个函数,求值时不能忽视x的取值范围.正解:当x≥0时,由x2-1=3,得x=2或x=-2(舍去);当x<0时,由2x+1=3,得x=1 (舍去),故x=2.
纠错心得:对于分段函数分为几部分应看成一个整体才有意义,它的定义域应是各部分x范围的并集,求某个自变量的函数值,容易不看自变量的范围直接代入解析式而求错解.1.分段函数求值要先找准自变量所在的区间;分段函数的定义域、值域分别是各段函数的定义域、值域的并集.
2.判断一个对应是不是映射,先看第一集合A:看集合A中的每一个元素是否都有对应元素,若有,再看对应元素是否唯一;至于集合B中的元素不作任何要求.课堂总结
