1.2.2函数的表示第二课时课件
文档属性
| 名称 | 1.2.2函数的表示第二课时课件 |  | |
| 格式 | zip | ||
| 文件大小 | 347.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 14:38:27 | ||
图片预览




文档简介
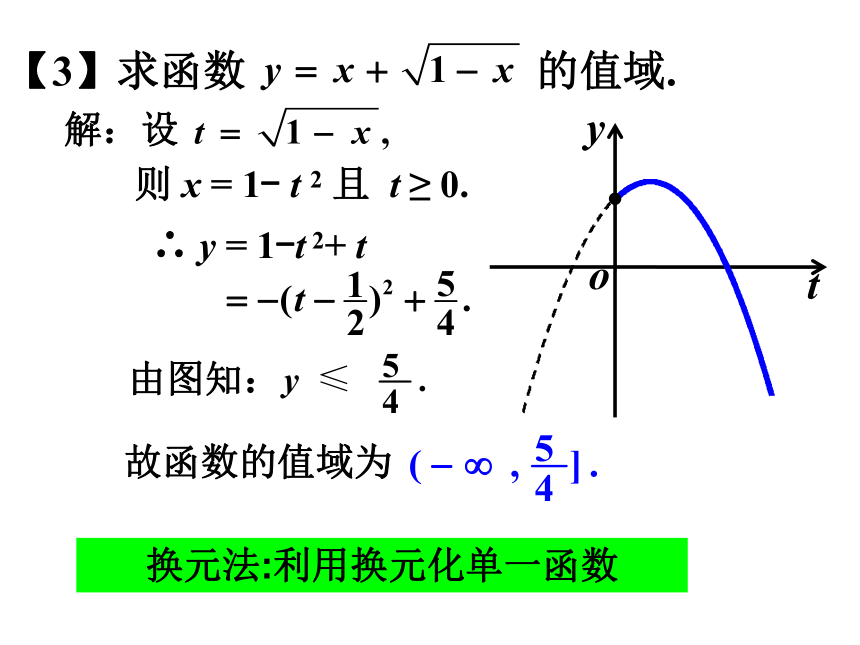
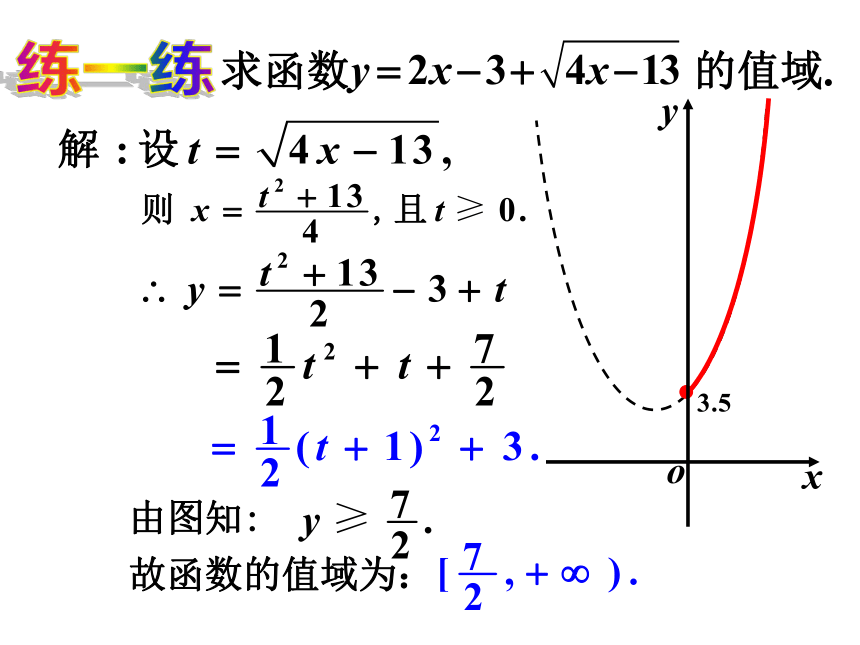
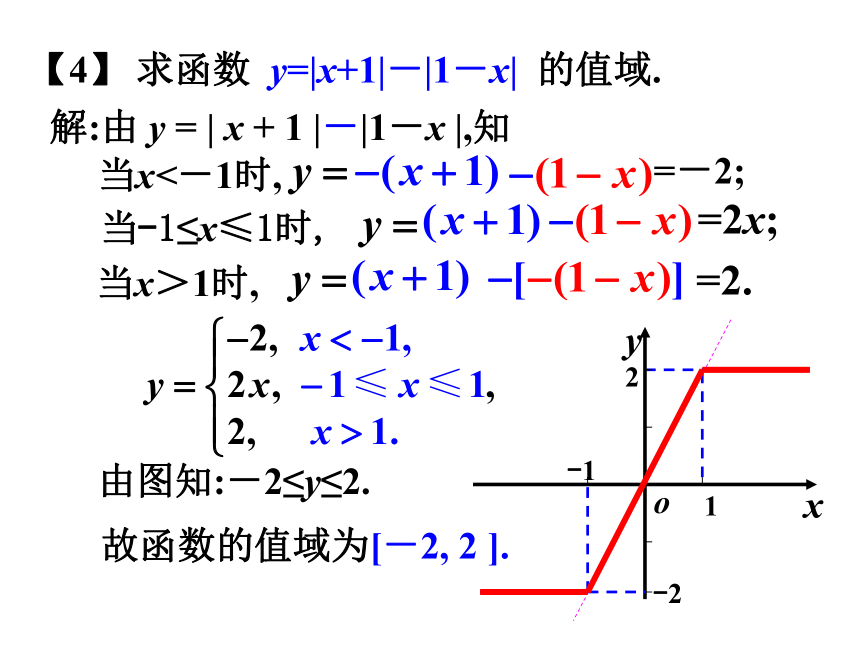
课件17张PPT。(二)1.2.2函数的表示法(1)学习了函数的三种表示方法;(3)学习了用函数知识解决实际问题.(5)数学思想方法的小结(2)函数的图象不仅可以是一段光滑的曲线还可以是一些孤立的点还可以是若干条线段; 数形结合的思想(4)学习了分段函数.复习回顾分类讨论的思想转化等思想.【1】求函数 的定义域.解: 依题意,有解之,得即所以函数的定义域是作业讲评C解析:函数的定义域满足解之,得【3】求函数 的值域.解:设 则 x = 1- t 2 且 t ≥ 0.∴ y = 1-t 2+ t 由图知:故函数的值域为换元法:利用换元化单一函数求函数 的值域.由图知:故函数的值域为:练一练【4】 求函数 y=|x+1|-|1-x| 的值域.解:由 y = | x + 1 |-|1-x |,知当x<-1时,当-1≤x≤1时, 当x>1时,由图知:-2≤y≤2.故函数的值域为[-2, 2 ].=-2;=2x;=2. 【1】已知函数若 f(x)=3, 则x的值是……………( ).A. 1B. C. D. D 变式练习 (1)分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
(2)分段函数在定义域的不同部分有不同的对应关系,但它是一个函数. 解:由题y = | x + 5 | + | x -1 | 当 x ≤-5 时,y = -( x + 5 ) -( x -1 )=-2x-4当 -5 < x ≤ 1 时,y = ( x + 5 ) -( x -1 ) = 6当 x >1 时,y = ( x + 5 ) + ( x -1 ) = 2x + 4【2】 化简函数变式练习(1) y=2x–1(3
2. 根据实际问题中的条件列出函数解析式,然后解决实际问题.
教材P23 练习T3.作业布置(1)求函数y = | 2x+1 | + | x -2 |值域 (1)当k=0时, 3≠0成立解:再见
(2)分段函数在定义域的不同部分有不同的对应关系,但它是一个函数. 解:由题y = | x + 5 | + | x -1 | 当 x ≤-5 时,y = -( x + 5 ) -( x -1 )=-2x-4当 -5 < x ≤ 1 时,y = ( x + 5 ) -( x -1 ) = 6当 x >1 时,y = ( x + 5 ) + ( x -1 ) = 2x + 4【2】 化简函数变式练习(1) y=2x–1(3
2. 根据实际问题中的条件列出函数解析式,然后解决实际问题.
教材P23 练习T3.作业布置(1)求函数y = | 2x+1 | + | x -2 |值域 (1)当k=0时, 3≠0成立解:再见
