人教A版(2019)高中数学选择性必修第一册 《椭圆》能力探究课件(共22张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 《椭圆》能力探究课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
人教A版同步教材名师课件
椭圆
---能力探究
椭圆及其标准方程
1.判断椭圆类型的方法
中心在原点、焦点分别在轴上、轴上的椭圆标准方程的
相同点:形状相同、大小相同;都有.
不同点:两种椭圆相对于坐标系的位置不同,它们的焦点坐标也不同(第一个椭圆的焦点坐标为和,,第二个椭圆的焦点坐标为和.椭圆的焦点在轴上标准方程中项的分母较大;椭圆的焦点在轴上标准方程中项的分母较大.
推测解释能力、分析计算能力
2.与椭圆几何性质有关的问题
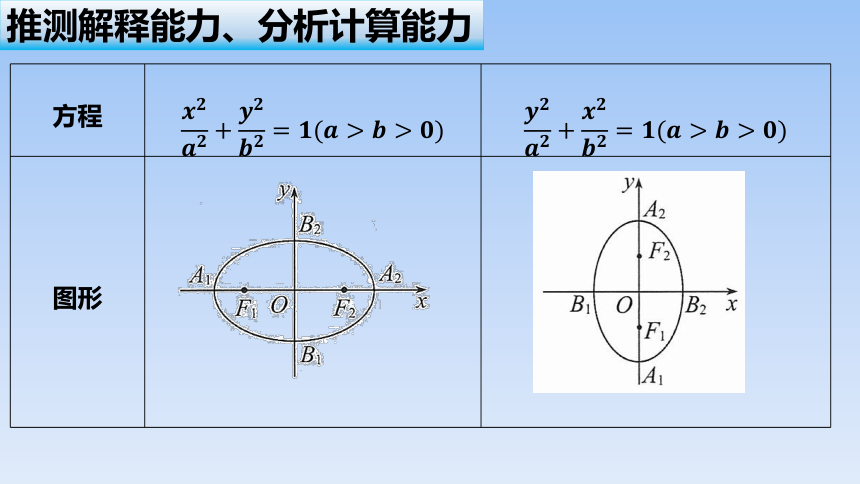
椭圆的几何性质可分为两类:一类是与坐标系有关的性质,如顶点、焦点、中心坐标;一类是与坐标系无关的本身固有性质,如长轴长、短轴长、焦距、离心率.对于第一类性质,只要的有关性质中横坐标和纵坐标互换,就可以得出的有关性质.总结如下:
推测解释能力、分析计算能力
推测解释能力、分析计算能力
方程
图形
推测解释能力、分析计算能力
方程
范围
对称性 关于x轴,y轴,坐标原点对称 关于x轴,y轴,坐标原点对称
顶点
离心率
说明:
(1)长轴:线段,长为;短轴:线段,长为;焦点在长轴上.
(2)对于离心率,因为,所以,离心率反映了椭圆的扁平程度.
由于,所以越趋近于越趋近于0,椭圆越扁平;越趋近于越趋近于,椭圆越趋近于圆.
推测解释能力、分析计算能力
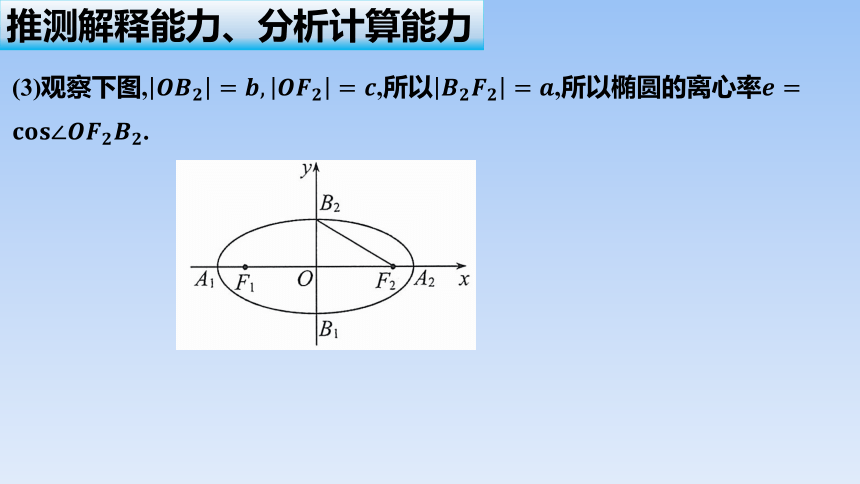
(3)观察下图,,所以,所以椭圆的离心率.
推测解释能力、分析计算能力
3.解决焦点三角形问题的常用方法
椭圆中的焦点三角形:通常结合定义、正弦定理、余弦定理、勾股定理来解决.
椭圆上一点和焦点为顶点的中,,则当为短轴端点时最大,且
(1).
(2).
(3).
推测解释能力、分析计算能力
典型例题
典例1-1 椭圆的一个顶点为,其长轴长是短轴长的2倍,求椭圆的标准方程.
(1)当为长轴端点时,,椭圆的标准方程为;
(2)当为短轴端点时,,椭圆的标准方程为.
解析
逻辑推理
题目没有指出焦点的位置,要考虑两种位置分类谈论.
思路
典型例题
典例1-2 若椭圆的离心率为,则______.
通过分析,无法确定题中椭圆焦点的位置,因而要两种情况分类讨论和计算.
当时,.
∴.
当时,,
∴.
解析
数学运算、逻辑推理
或2
典型例题
典例1-3 是椭圆上的一点,和为左右焦点,若.
(1)求的面积;(2)求点的坐标.
(1)∵.
设,则,①
.②
由,得..
解析
数学运算、逻辑推理
本题在焦点三角形中利用椭圆定义、余弦定理和三角形的面积公式综合解题.
思路
典型例题
典例1-3 是椭圆上的一点,和为左右焦点,若.
(1)求的面积;(2)求点的坐标.
(2)设,由,得.
将代入椭圆方程解得,∴,或,或,或.
数学运算、逻辑推理
解析
典型例题
典例1-4 与椭圆有相同焦点,且过点的椭圆方程为________.
由于两个椭圆的焦点相同,所以可采用待定系数法,利用共焦点的椭圆系方程求解.
由题意可设椭圆的方程为.
又所求椭圆过点,
所以将(代入椭圆方程,得,解得(舍去).
故所求的椭圆方程为.
解析
数学运算
综合问题解决能力
椭圆的简单几何性质
1.研究直线与椭圆位置关系的思路
(1)研究直线与椭圆的位置关系,可联立直线与椭圆的方程,消元后用判别式讨论.
(2)求直线被椭圆截得的弦长,一般利用弦长公式,对于与坐标轴平行的直线,直接求交点坐标即可求解.
(3)有关弦长的最值问题,可以运用二次函数性质、一元二次方程的判别式、基本不等式等来求解.
综合问题解决能力
2.椭圆的中点弦问题
(1)求解中点弦问题的关键在于充分利用“中点”这一条件,灵活运用中点坐标公式及根与系数的关系.求解此类问题常用“设而不求”的思想方法,即设出交点坐标,代入方程,整体求解.
(2)掌握好直线与椭圆相交时的常见处理方法,如当直线与椭圆相交时:涉及弦长问题,常用“根与系数的关系”,设而不求计算弦长;涉及求平行弦中点的轨迹、求过定点的弦中点的轨迹和求被定点平分的弦所在的直线方程问题,常用“点差法”设而不求,将动点的坐标、弦所在直线的斜率、弦的中点坐标联系起来,相互转化.
综合问题解决能力
3.与椭圆有关的定值、定点问题
方法总结:解决与椭圆有关的定值、定点问题常利用设而不求的思想方法.将相关量设出→利用椭圆的几何性质将所求值或点表示出来→说明要求解的量与变量的取值无关.
综合问题解决能力
注意:
(1)椭圆定点、定值问题的两类基本形式:①椭圆中满足一定条件的两点连接所得的直线经过定点;②椭圆中与满足一定条件的两点有关的几何量为定值,两者往往可以互相转化.
(2)在椭圆综合问题中,某些几何量与参数无关,构成了定点、定值问题的基础,解决此类问题的方法一般是:①计算推理求其结果;②考虑极端或特殊位置,探索出定点定值后予以证明.
综合问题解决能力
4.与椭圆有关的实际应用问题
解与椭圆有关的实际应用问题时,首先要抽象出相应的数学问题,即所谓的建数学模型,然后解决这个数学问题,与椭圆有关的实际应用主要体现在定义的应用,a、b、c之间相互关系的应用,图形自身特征的应用等.
典型例题
典例2 过点作直线与椭圆相交于、两点,为坐标原点,求面积的最大值及此时直线倾斜角的正切值.
直观想象、数学运算
本题若直接用点斜式设的方程为,则要求的斜率一定要存在,但在这里的斜率有可能不存在,因此要讨论斜率不存在的情形,为了避免讨论,我们可以设直线的方程为,这样就包含了斜率不存在时的情形了,从而简化了运算.
思路
典型例题
典例2 过点作直线与椭圆相交于、两点,为坐标原点,求面积的最大值及此时直线倾斜角的正切值.
设,
,
把代入椭圆方程得:即
,
直观想象、数学运算
解析
典型例题
典例2 过点作直线与椭圆相交于、两点,为坐标原点,求面积的最大值及此时直线倾斜角的正切值.
,
直观想象、数学运算
解析
典型例题
典例2 过点作直线与椭圆相交于、两点,为坐标原点,求面积的最大值及此时直线倾斜角的正切值.
∴此时,,
令直线的倾角为,则,即面积的最大值为,此时直线倾斜角的正切值为.
直观想象、数学运算
解析
人教A版同步教材名师课件
椭圆
---能力探究
椭圆及其标准方程
1.判断椭圆类型的方法
中心在原点、焦点分别在轴上、轴上的椭圆标准方程的
相同点:形状相同、大小相同;都有.
不同点:两种椭圆相对于坐标系的位置不同,它们的焦点坐标也不同(第一个椭圆的焦点坐标为和,,第二个椭圆的焦点坐标为和.椭圆的焦点在轴上标准方程中项的分母较大;椭圆的焦点在轴上标准方程中项的分母较大.
推测解释能力、分析计算能力
2.与椭圆几何性质有关的问题
椭圆的几何性质可分为两类:一类是与坐标系有关的性质,如顶点、焦点、中心坐标;一类是与坐标系无关的本身固有性质,如长轴长、短轴长、焦距、离心率.对于第一类性质,只要的有关性质中横坐标和纵坐标互换,就可以得出的有关性质.总结如下:
推测解释能力、分析计算能力
推测解释能力、分析计算能力
方程
图形
推测解释能力、分析计算能力
方程
范围
对称性 关于x轴,y轴,坐标原点对称 关于x轴,y轴,坐标原点对称
顶点
离心率
说明:
(1)长轴:线段,长为;短轴:线段,长为;焦点在长轴上.
(2)对于离心率,因为,所以,离心率反映了椭圆的扁平程度.
由于,所以越趋近于越趋近于0,椭圆越扁平;越趋近于越趋近于,椭圆越趋近于圆.
推测解释能力、分析计算能力
(3)观察下图,,所以,所以椭圆的离心率.
推测解释能力、分析计算能力
3.解决焦点三角形问题的常用方法
椭圆中的焦点三角形:通常结合定义、正弦定理、余弦定理、勾股定理来解决.
椭圆上一点和焦点为顶点的中,,则当为短轴端点时最大,且
(1).
(2).
(3).
推测解释能力、分析计算能力
典型例题
典例1-1 椭圆的一个顶点为,其长轴长是短轴长的2倍,求椭圆的标准方程.
(1)当为长轴端点时,,椭圆的标准方程为;
(2)当为短轴端点时,,椭圆的标准方程为.
解析
逻辑推理
题目没有指出焦点的位置,要考虑两种位置分类谈论.
思路
典型例题
典例1-2 若椭圆的离心率为,则______.
通过分析,无法确定题中椭圆焦点的位置,因而要两种情况分类讨论和计算.
当时,.
∴.
当时,,
∴.
解析
数学运算、逻辑推理
或2
典型例题
典例1-3 是椭圆上的一点,和为左右焦点,若.
(1)求的面积;(2)求点的坐标.
(1)∵.
设,则,①
.②
由,得..
解析
数学运算、逻辑推理
本题在焦点三角形中利用椭圆定义、余弦定理和三角形的面积公式综合解题.
思路
典型例题
典例1-3 是椭圆上的一点,和为左右焦点,若.
(1)求的面积;(2)求点的坐标.
(2)设,由,得.
将代入椭圆方程解得,∴,或,或,或.
数学运算、逻辑推理
解析
典型例题
典例1-4 与椭圆有相同焦点,且过点的椭圆方程为________.
由于两个椭圆的焦点相同,所以可采用待定系数法,利用共焦点的椭圆系方程求解.
由题意可设椭圆的方程为.
又所求椭圆过点,
所以将(代入椭圆方程,得,解得(舍去).
故所求的椭圆方程为.
解析
数学运算
综合问题解决能力
椭圆的简单几何性质
1.研究直线与椭圆位置关系的思路
(1)研究直线与椭圆的位置关系,可联立直线与椭圆的方程,消元后用判别式讨论.
(2)求直线被椭圆截得的弦长,一般利用弦长公式,对于与坐标轴平行的直线,直接求交点坐标即可求解.
(3)有关弦长的最值问题,可以运用二次函数性质、一元二次方程的判别式、基本不等式等来求解.
综合问题解决能力
2.椭圆的中点弦问题
(1)求解中点弦问题的关键在于充分利用“中点”这一条件,灵活运用中点坐标公式及根与系数的关系.求解此类问题常用“设而不求”的思想方法,即设出交点坐标,代入方程,整体求解.
(2)掌握好直线与椭圆相交时的常见处理方法,如当直线与椭圆相交时:涉及弦长问题,常用“根与系数的关系”,设而不求计算弦长;涉及求平行弦中点的轨迹、求过定点的弦中点的轨迹和求被定点平分的弦所在的直线方程问题,常用“点差法”设而不求,将动点的坐标、弦所在直线的斜率、弦的中点坐标联系起来,相互转化.
综合问题解决能力
3.与椭圆有关的定值、定点问题
方法总结:解决与椭圆有关的定值、定点问题常利用设而不求的思想方法.将相关量设出→利用椭圆的几何性质将所求值或点表示出来→说明要求解的量与变量的取值无关.
综合问题解决能力
注意:
(1)椭圆定点、定值问题的两类基本形式:①椭圆中满足一定条件的两点连接所得的直线经过定点;②椭圆中与满足一定条件的两点有关的几何量为定值,两者往往可以互相转化.
(2)在椭圆综合问题中,某些几何量与参数无关,构成了定点、定值问题的基础,解决此类问题的方法一般是:①计算推理求其结果;②考虑极端或特殊位置,探索出定点定值后予以证明.
综合问题解决能力
4.与椭圆有关的实际应用问题
解与椭圆有关的实际应用问题时,首先要抽象出相应的数学问题,即所谓的建数学模型,然后解决这个数学问题,与椭圆有关的实际应用主要体现在定义的应用,a、b、c之间相互关系的应用,图形自身特征的应用等.
典型例题
典例2 过点作直线与椭圆相交于、两点,为坐标原点,求面积的最大值及此时直线倾斜角的正切值.
直观想象、数学运算
本题若直接用点斜式设的方程为,则要求的斜率一定要存在,但在这里的斜率有可能不存在,因此要讨论斜率不存在的情形,为了避免讨论,我们可以设直线的方程为,这样就包含了斜率不存在时的情形了,从而简化了运算.
思路
典型例题
典例2 过点作直线与椭圆相交于、两点,为坐标原点,求面积的最大值及此时直线倾斜角的正切值.
设,
,
把代入椭圆方程得:即
,
直观想象、数学运算
解析
典型例题
典例2 过点作直线与椭圆相交于、两点,为坐标原点,求面积的最大值及此时直线倾斜角的正切值.
,
直观想象、数学运算
解析
典型例题
典例2 过点作直线与椭圆相交于、两点,为坐标原点,求面积的最大值及此时直线倾斜角的正切值.
∴此时,,
令直线的倾角为,则,即面积的最大值为,此时直线倾斜角的正切值为.
直观想象、数学运算
解析
