高一数学 1.2.3 《空间中的垂直关系(1)》课件 新人教A版必修2
文档属性
| 名称 | 高一数学 1.2.3 《空间中的垂直关系(1)》课件 新人教A版必修2 |  | |
| 格式 | zip | ||
| 文件大小 | 95.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 14:01:28 | ||
图片预览








文档简介
课件23张PPT。1.2.3 空间中的垂直关系(1)一. 直线与平面垂直的定义1. 两直线互相垂直:
如果两条直线相交于一点或经过平移后相交于一点,并且交角为直角,则称这两条直线互相垂直。 观察旗杆与地面内的每一条直线有什么关系,旗杆与地面的关系呢?2. 直线与平面垂直:
如果一条直线(l)和一个平面(α)相交于点A,并且a和这个平面内过点A的任何直线都垂直,则该直线垂直于这个平面,记作l⊥α,这条直线叫做平面的垂线,这个平面叫做直线的垂面,交点叫做垂足。 在几何中,定义兼具两重性,既是判定又是性质。判定是指:如果一条直线垂直一个平面内的任意一条直线,那么这条直线与这个平面垂直,这是判定证明直线与平面垂直的一种方法;性质是指:如果一条直线垂直于一个平面,那么这条直线垂直于这个平面内的任意一条直线。 这是在线面垂直问题中经常要用到的一个结论。即判断正误:
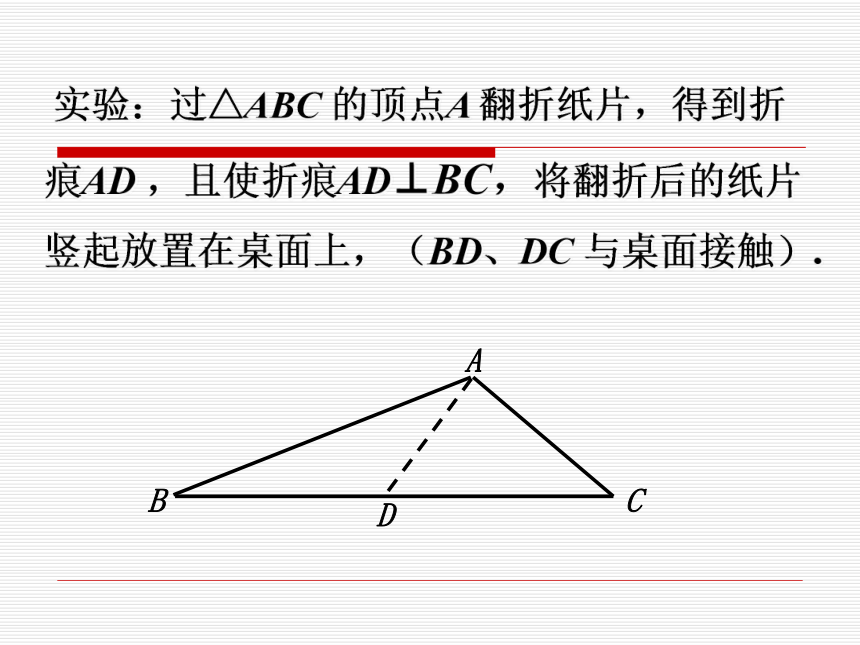
如果一条直线 l 和一个平面内的无数条直线都垂直,则直线 l和平面 α互相垂直.二. 直线与平面垂直的判定定理1.定理:
①文字语言:如果一条直线与平面内的两条相交直线垂直,则这条直线与这个平面垂直.②图形语言:③符号语言:a α,b α,a∩b=O,l⊥a,l⊥b, l⊥α. 实验:过△ABC 的顶点A 翻折纸片,得到折痕AD ,且使折痕AD⊥BC,将翻折后的纸片竖起放置在桌面上,(BD、DC 与桌面接触).证明:设m是α内的任意一条直线. 推论1 :如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面. 推论2:如果两条直线垂直于同一个平面,那么这两条直线平行 。已知:直线l⊥平面α,直线m⊥平面α,垂足分别为a,b,求证:l//m.证明:假设直线m与直线l不平行。过直线m与平面α的交点B作直线m’//l,由直线与平面垂直的判定定理的推论1可知m’⊥α. 设m和m’确定的平面为β,α与β的交线为a,因为直线m和m’都垂直于平面α,所以 直线m和m’都垂直于交线a,因为在同一平面内,通过直线上一点并与已知直线垂直的直线不可能有两条,所以直线m与m’必重合,
即有l //m.例1.过一点和已知平面垂直的直线只有一条。已知:平面α和一点P.
求证:过点P与α垂直的直线只有一条。证明:不论P点在α外或内,设PA⊥α,垂足为A(或P), 如果过P点,除直线PA⊥α外,还有一条直线PB⊥α,设PA,PB确定的平面为β, 且α∩β=a, 于是在平面β内过点P有两条直线PA,PB垂直于交线a, 这是不可能的。所以过点P与α垂直的直线只有一条。例1、有一根旗杆AB高8m,它的顶端A挂有一条长10m的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一条直线上)C、D, 如果这两点都和旗杆脚B的距离是6m,那么旗杆就和地面垂直,为什么?解:在△ABC和△ABD中,因为AB=8,BC=BD=6,AC=AD=10,所以 AB2+BC2=82+62=102=AC2. AB2+BD2=82+62=102=AD2. 所以∠ABC=∠ABD=90°, 即AB⊥BC,AB⊥BD, 又知B,C,D三点不共线,因此AB⊥平面BCD,即旗杆和地面垂直。例3.已知:直线l⊥平面α,垂足为A,直线AP⊥l. 求证:AP在α内。证明:设AP与l 确定的平面为β,假设AP不在α内,
则设α与β相交于直线AM。因为l⊥α,AM α,所以l⊥AM,又已知AP⊥l,于是在平面β内,
过点A有两条直线垂直于l,
这是不可能的,所以AP一定在α内。直线与平面垂直的判定方法3.如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。1.定义:如果一条直线垂于一个平面内的任何一条直线,则此直线垂直于这个平面.2.判定定理:如果一条直线垂直于一个平面内的两条相交直线,那么此直线垂直于这个平面。4.如果直线和平面所成的角等于90°,则这条直线和平面垂直练习题: 1 、如果平面外的一条直线上有两点到这个平面的距离相等,则这条直线和平面的位置关系是( ) A.平行 B.相交 C.平行或相交C2、在空间,下列命题(1)平行于同一直线的两条直线互相平行;(2)垂直于同一直线的两条直线互相平行;(3)平行于同一平面的两条直线互相平行;(4)垂直于同一平面的两条直线互相平行。正确的是( )A. (1)(3)(4) B. (1)(4)
C. (1) D.四个命题都正确。B3. 如图,正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,求证:B1H⊥平面AD1C.证明:连接B1D1,
∵ B1B⊥AB,B1B⊥BC,
∴ B1B⊥平面ABCD,
∴ B1B⊥AC,∵ 又AC⊥BD, ∴ AC⊥平面BB1D1D,
又B1H平面BB1D1D,∴ AC⊥B1H,
又B1H⊥D1O,∴ B1H⊥平面AD1C.
如果两条直线相交于一点或经过平移后相交于一点,并且交角为直角,则称这两条直线互相垂直。 观察旗杆与地面内的每一条直线有什么关系,旗杆与地面的关系呢?2. 直线与平面垂直:
如果一条直线(l)和一个平面(α)相交于点A,并且a和这个平面内过点A的任何直线都垂直,则该直线垂直于这个平面,记作l⊥α,这条直线叫做平面的垂线,这个平面叫做直线的垂面,交点叫做垂足。 在几何中,定义兼具两重性,既是判定又是性质。判定是指:如果一条直线垂直一个平面内的任意一条直线,那么这条直线与这个平面垂直,这是判定证明直线与平面垂直的一种方法;性质是指:如果一条直线垂直于一个平面,那么这条直线垂直于这个平面内的任意一条直线。 这是在线面垂直问题中经常要用到的一个结论。即判断正误:
如果一条直线 l 和一个平面内的无数条直线都垂直,则直线 l和平面 α互相垂直.二. 直线与平面垂直的判定定理1.定理:
①文字语言:如果一条直线与平面内的两条相交直线垂直,则这条直线与这个平面垂直.②图形语言:③符号语言:a α,b α,a∩b=O,l⊥a,l⊥b, l⊥α. 实验:过△ABC 的顶点A 翻折纸片,得到折痕AD ,且使折痕AD⊥BC,将翻折后的纸片竖起放置在桌面上,(BD、DC 与桌面接触).证明:设m是α内的任意一条直线. 推论1 :如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面. 推论2:如果两条直线垂直于同一个平面,那么这两条直线平行 。已知:直线l⊥平面α,直线m⊥平面α,垂足分别为a,b,求证:l//m.证明:假设直线m与直线l不平行。过直线m与平面α的交点B作直线m’//l,由直线与平面垂直的判定定理的推论1可知m’⊥α. 设m和m’确定的平面为β,α与β的交线为a,因为直线m和m’都垂直于平面α,所以 直线m和m’都垂直于交线a,因为在同一平面内,通过直线上一点并与已知直线垂直的直线不可能有两条,所以直线m与m’必重合,
即有l //m.例1.过一点和已知平面垂直的直线只有一条。已知:平面α和一点P.
求证:过点P与α垂直的直线只有一条。证明:不论P点在α外或内,设PA⊥α,垂足为A(或P), 如果过P点,除直线PA⊥α外,还有一条直线PB⊥α,设PA,PB确定的平面为β, 且α∩β=a, 于是在平面β内过点P有两条直线PA,PB垂直于交线a, 这是不可能的。所以过点P与α垂直的直线只有一条。例1、有一根旗杆AB高8m,它的顶端A挂有一条长10m的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一条直线上)C、D, 如果这两点都和旗杆脚B的距离是6m,那么旗杆就和地面垂直,为什么?解:在△ABC和△ABD中,因为AB=8,BC=BD=6,AC=AD=10,所以 AB2+BC2=82+62=102=AC2. AB2+BD2=82+62=102=AD2. 所以∠ABC=∠ABD=90°, 即AB⊥BC,AB⊥BD, 又知B,C,D三点不共线,因此AB⊥平面BCD,即旗杆和地面垂直。例3.已知:直线l⊥平面α,垂足为A,直线AP⊥l. 求证:AP在α内。证明:设AP与l 确定的平面为β,假设AP不在α内,
则设α与β相交于直线AM。因为l⊥α,AM α,所以l⊥AM,又已知AP⊥l,于是在平面β内,
过点A有两条直线垂直于l,
这是不可能的,所以AP一定在α内。直线与平面垂直的判定方法3.如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面。1.定义:如果一条直线垂于一个平面内的任何一条直线,则此直线垂直于这个平面.2.判定定理:如果一条直线垂直于一个平面内的两条相交直线,那么此直线垂直于这个平面。4.如果直线和平面所成的角等于90°,则这条直线和平面垂直练习题: 1 、如果平面外的一条直线上有两点到这个平面的距离相等,则这条直线和平面的位置关系是( ) A.平行 B.相交 C.平行或相交C2、在空间,下列命题(1)平行于同一直线的两条直线互相平行;(2)垂直于同一直线的两条直线互相平行;(3)平行于同一平面的两条直线互相平行;(4)垂直于同一平面的两条直线互相平行。正确的是( )A. (1)(3)(4) B. (1)(4)
C. (1) D.四个命题都正确。B3. 如图,正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,求证:B1H⊥平面AD1C.证明:连接B1D1,
∵ B1B⊥AB,B1B⊥BC,
∴ B1B⊥平面ABCD,
∴ B1B⊥AC,∵ 又AC⊥BD, ∴ AC⊥平面BB1D1D,
又B1H平面BB1D1D,∴ AC⊥B1H,
又B1H⊥D1O,∴ B1H⊥平面AD1C.
