高一数学 1.3.1 函数的单调性课件 新一课件 新人教A版必修1
文档属性
| 名称 | 高一数学 1.3.1 函数的单调性课件 新一课件 新人教A版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 14:31:53 | ||
图片预览

文档简介
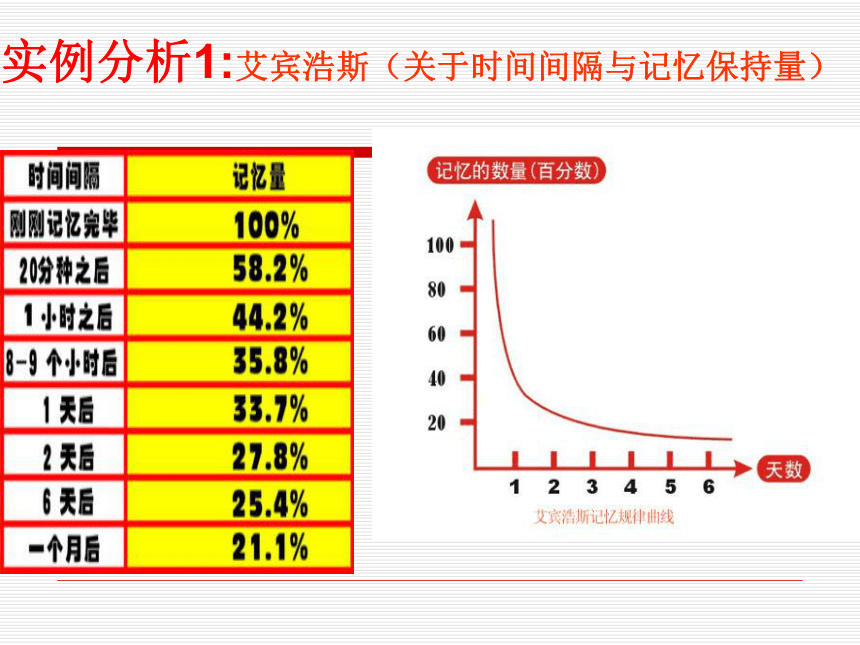
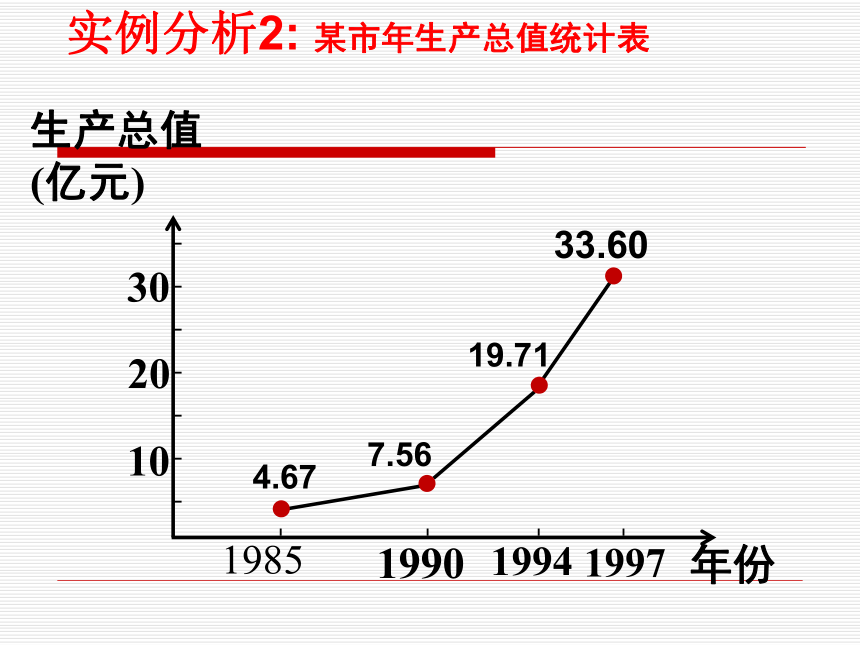
课件17张PPT。1.3 函数的基本性质1.3.1函数的单调性 实例分析1:艾宾浩斯(关于时间间隔与记忆保持量)实例分析2: 某市年生产总值统计表生产总值
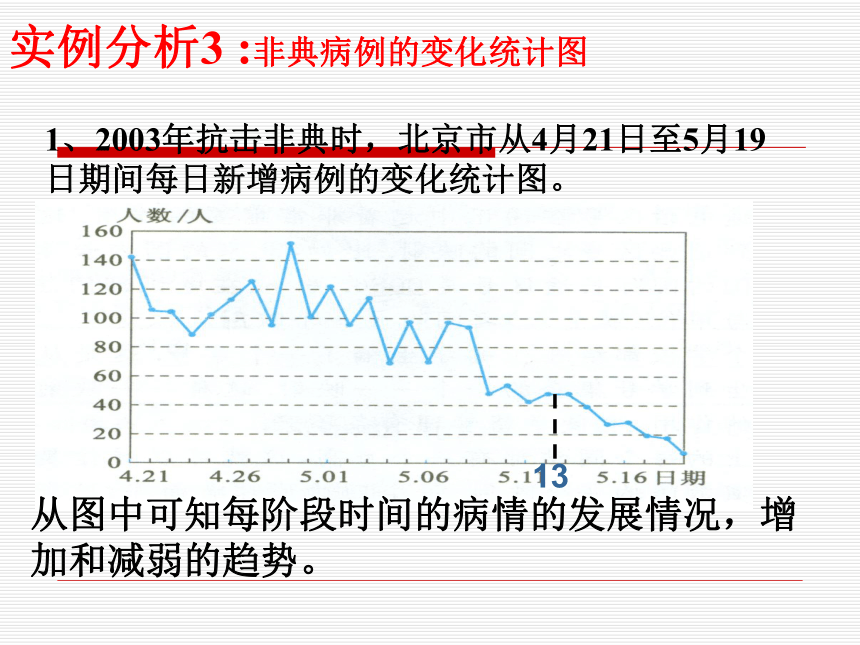
(亿元)年份30201033.6019.717.564.67实例分析3 :非典病例的变化统计图
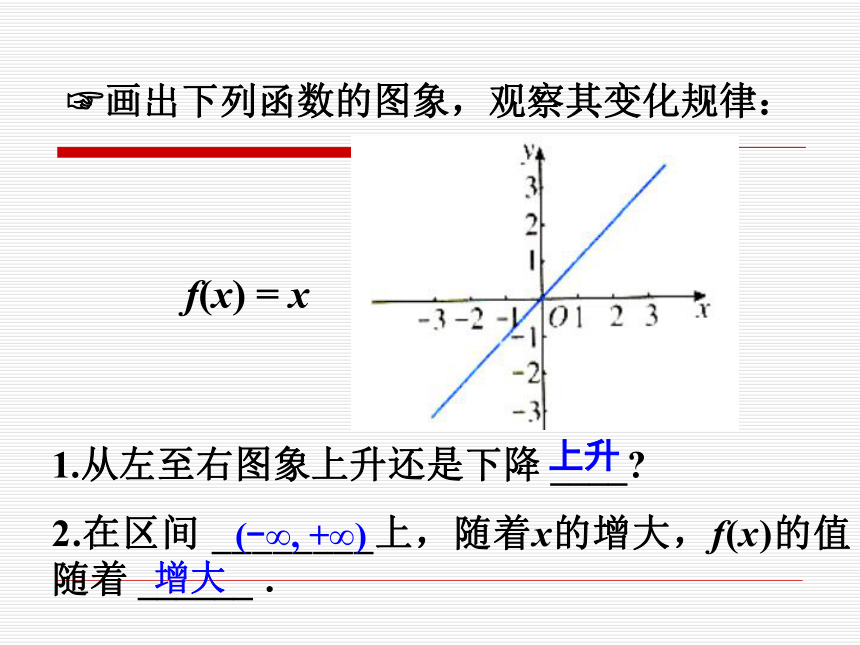
1、2003年抗击非典时,北京市从4月21日至5月19日期间每日新增病例的变化统计图。从图中可知每阶段时间的病情的发展情况,增加和减弱的趋势。13?画出下列函数的图象,观察其变化规律: 1.从左至右图象上升还是下降 ____?
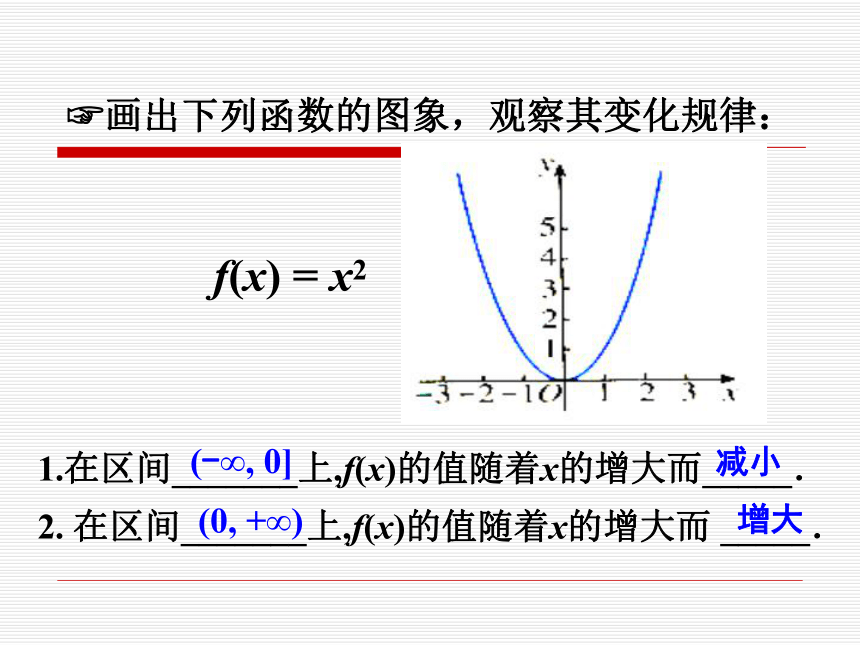
2.在区间 ________上,随着x的增大,f(x)的值随着 ______ .f(x) = x(-∞, +∞)增大上升1.在区间_______上,f(x)的值随着x的增大而_____.
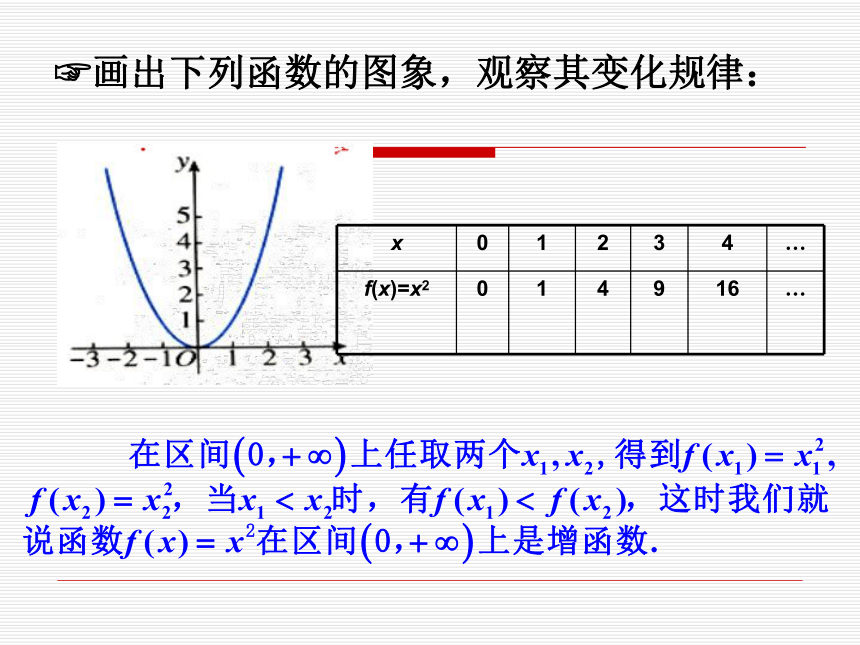
2. 在区间_______上,f(x)的值随着x的增大而 _____. f(x) = x2(-∞, 0](0, +∞)增大减小?画出下列函数的图象,观察其变化规律: ?画出下列函数的图象,观察其变化规律: 一、函数单调性定义 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1f(x2),那么就说f(x)在区间D上是减函数 .2.减函数 2.函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;注意: 1.必须是对于区间D内的任意两个自变量x1,x2;当x1f(x2) 分别是增函数和减函数.例1.下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?解:函数y=f(x)的单调区间有其中y=f(x)在区间[-5, -2), [1, 3)上是减函数,
在区间[-2, 1), [3, 5] 上是增函数.[-5, -2), [-2,1), [1, 3), [3, 5]. 二.典例精析例2.证明:函数 在 上是增函数.思考:如何证明一个函数是单调递增的呢?取值判号定论三、判断函数单调性的方法步骤 ①取值: 任取x1,x2∈D,且x1②作差:f(x1)-f(x2);
③变形:(因式分解和配方等)乘积或商式;
④定号:(即判断差f(x1)-f(x2)的正负);
⑤下结论:(即指出函数f(x)在给定的区间D上的单调性). 利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:四、归纳小结 3.函数单调性的证明,证明一般分五步:
取 值 → 作 差 → 化简 → 判号 → 下结论
2.会利用函数图像找出函数的单调区间1.函数单调性的定义必做:?课本P39 习题1.3(A组)
第2题.五、作业选做:?课本P39 习题1.3(A组) 第3题.祝同学们学习快乐!
再见!
2010.9.26证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V10, V2- V1 >0取值定号结论定号
(亿元)年份30201033.6019.717.564.67实例分析3 :非典病例的变化统计图
1、2003年抗击非典时,北京市从4月21日至5月19日期间每日新增病例的变化统计图。从图中可知每阶段时间的病情的发展情况,增加和减弱的趋势。13?画出下列函数的图象,观察其变化规律: 1.从左至右图象上升还是下降 ____?
2.在区间 ________上,随着x的增大,f(x)的值随着 ______ .f(x) = x(-∞, +∞)增大上升1.在区间_______上,f(x)的值随着x的增大而_____.
2. 在区间_______上,f(x)的值随着x的增大而 _____. f(x) = x2(-∞, 0](0, +∞)增大减小?画出下列函数的图象,观察其变化规律: ?画出下列函数的图象,观察其变化规律: 一、函数单调性定义 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
在区间[-2, 1), [3, 5] 上是增函数.[-5, -2), [-2,1), [1, 3), [3, 5]. 二.典例精析例2.证明:函数 在 上是增函数.思考:如何证明一个函数是单调递增的呢?取值判号定论三、判断函数单调性的方法步骤 ①取值: 任取x1,x2∈D,且x1
③变形:(因式分解和配方等)乘积或商式;
④定号:(即判断差f(x1)-f(x2)的正负);
⑤下结论:(即指出函数f(x)在给定的区间D上的单调性). 利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:四、归纳小结 3.函数单调性的证明,证明一般分五步:
取 值 → 作 差 → 化简 → 判号 → 下结论
2.会利用函数图像找出函数的单调区间1.函数单调性的定义必做:?课本P39 习题1.3(A组)
第2题.五、作业选做:?课本P39 习题1.3(A组) 第3题.祝同学们学习快乐!
再见!
2010.9.26证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1
