高一数学 2.1.2 指数函数及其性质课件 新人教A版必修1
文档属性
| 名称 | 高一数学 2.1.2 指数函数及其性质课件 新人教A版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 460.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 14:58:17 | ||
图片预览











文档简介
课件45张PPT。2.1 指数函数2.1.2 指数函数及其性质第1课时
指数函数的概念、图象及性质1.理解指数函数的概念和意义,能借助计算器或计算机画出指数函数图象.
2.初步掌握指数函数的有关性质.
3.在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型.研 习 新 知新 知 视 界
1.函数y=ax(a>0且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.
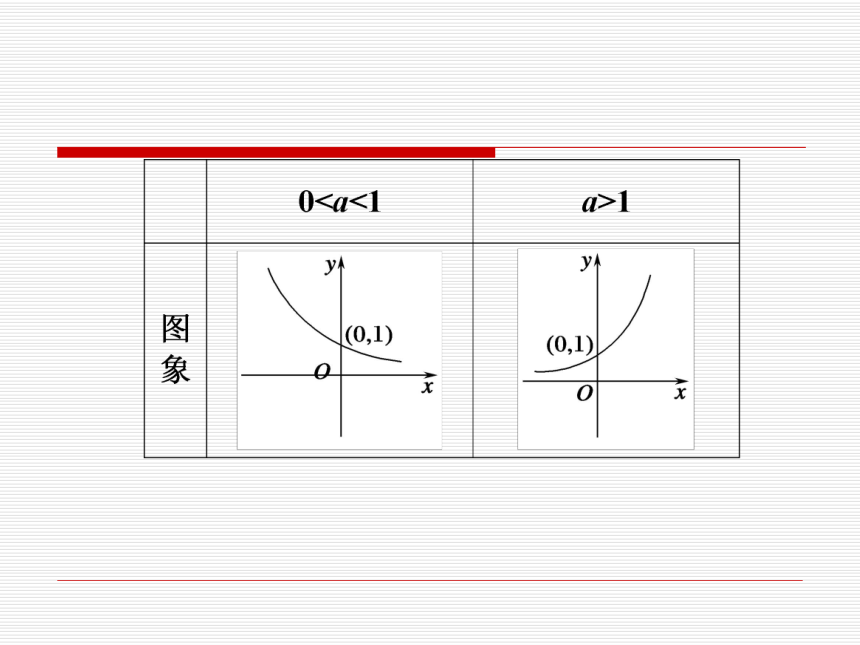
2.指数函数y=ax(a>0且a≠1)的图象和性质用下表表示:3.底数a对图象的影响:在同一坐标系中,当a>1时,a越大,y轴右边的图象越靠近y轴,即底数越大,x>0时,函数值增长越快;当0 1.为什么在指数函数y=ax中规定底数a大于零且不等1?
提示:(1)如果a=0,当x>0时,ax恒等于0;当x≤0时,ax无意义.自 我 检 测
1.下列一定是指数函数的是( )
A.形如y=ax的函数 B.y=xa(a>0,且a≠1)
C.y=(|a|+2)x D.y=(a-2)ax
解析:∵y=(|a|+2)x符合指数函数的定义,
∴y=(|a|+2)x是指数函数.
答案:C2.指数函数y=ax与y=bx的图象如右图1,则( )
A.a<0,b<0
B.a<0,b>0
C.01
D.0解析:结合指数函数的图象知b>1,0答案:C
3.函数y=πx的值域是( )
A.(0,+∞) B.[0,+∞)
C.R D.(-∞,0)
答案:A4.函数y=(a-1)x在R上为减函数,则a的取值范围是________.
解析:∵y=(a-1)x在R上递减,
∴0答案:(1,2)
5.已知指数函数f(x)的图象过点(3,8),求f(6)的值.
解:设f(x)=ax,则a3=8,∴a=2,∴f(x)=2x,∴f(6)=26=64.互 动 课 堂 典 例 导 悟
类型一 指数函数的概念
[例1] 指出下列函数哪些是指数函数:
(1)y=4x;(2)y=x4;(3)y=-4x;(4)y=(-4)x;(5)y=4x2;(6)y=xx;(7)y=(2a-1)x(a>,且a≠1).
[分析] 根据指数函数的定义进行判断.[解] (1)(7)为指数函数.
(2)不是指数函数.
(3)是-1与指数函数4x的乘积,所以不是指数函数.
(4)中底数-4<0,所以不是指数函数.
(5)中指数不是自变量x,所以不是指数函数.
(6)中底数x不是常数,不符合指数函数的定义,所以不是指数函数.变式体验1 若y=(a-3)·(a-2)x是指数函数,求a的值.(2)由图象知函数在(-∞,-1]上是增函数,在[-1,+∞)上是减函数.
(3)由图象知当x=-1时,有最大值1,无最小值.
[点评] (1)指数型函数的作图一般从最基本的指数函数入手,通过平移、伸缩、对称变换得到.(2)带有绝对值的图象作图,一般分为两种情况,一种是去掉绝对值作图,一种是不去绝对值,如y=f(|x|)可依据函数是偶函数,先作出y=f(x)(x≥0)的图象,x<0时的图象只需将y=f(x)(x≥0)图象关于y轴对称过去即可,又如y=|f(x)|的图象,可作出y=f(x)的图象,保留x轴上方图象,将下方图象关于x轴对称过去即可得y=|f(x)|的图象.[点评] 本题中的函数都不是指数函数,但都与指数函数有关.根据指数函数的定义域为R,值域为(0,+∞),结合前一章求函数定义域和值域的方法,可以求解一些简单函数的定义域和值域.在求解中要注意正确运用指数函数的单调性.在求值域问题时,既要考虑指数函数的单调性,还应注意指数函数的值域为(0,+∞).类型四 比较大小
[例4] 比较下列各组数的大小:[分析] 因为是两个指数幂比较大小,故解答本题可利用指数函数的图象与性质或通过寻求第三个数,将两数进行比较.[点评] 比较幂的大小的常用方法:
(1)对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断.(2)对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图象的变化规律来判断.(3)对于底数不同,且指数也不同的幂的大小比较,则应通过中间值来比较.变式体验4 已知a=0.80.7,b=0.80.9,c=1.20.8,则a、b、c的大小关系是( )
A.a>b>c B.b>a>c
C.c>b>a D.c>a>b
解析:∵y=0.8x是减函数,∴a=0.80.7>0.80.9=b,且a=0.80.7<0.80=1.又c=1.20.8>1,∴c>a>b.故选D.
答案:D 思 悟 升 华
1.指数函数是形式化的概念,形如y=ax(a>0,且a≠1)的函数被称为指数函数,这里x是自变量,要判断一个函数是否是指数函数,需抓住三点:①底数大于零且不等于1;②幂指数有单一的自变量x;③系数为1,且没有其他的项.
2.当底数a大小不定时,必须分“a>1”和“01时,a的值越大,y轴右边的图象越靠近y轴,当0 4.指数函数y=ax(a>0且a≠1)的定义域是R,其值域是(0,+∞).
关于指数型函数y=af(x)+b的定义域可结合求函数定义域的方法,通过解不等式或不等式组来解决;求其值域可采用换元法,既要考虑指数函数的单调性,还应注意指数函数的值域是(0,+∞).5.比较幂值的大小常常化为同底数的幂,根据指数函数的单调性比较大小.如果不能化为同底数的幂,则要借助幂值的范围利用中间值过渡(常选1作中间值).课时作业(15)
指数函数的概念、图象及性质1.理解指数函数的概念和意义,能借助计算器或计算机画出指数函数图象.
2.初步掌握指数函数的有关性质.
3.在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型.研 习 新 知新 知 视 界
1.函数y=ax(a>0且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.
2.指数函数y=ax(a>0且a≠1)的图象和性质用下表表示:3.底数a对图象的影响:在同一坐标系中,当a>1时,a越大,y轴右边的图象越靠近y轴,即底数越大,x>0时,函数值增长越快;当0
提示:(1)如果a=0,当x>0时,ax恒等于0;当x≤0时,ax无意义.自 我 检 测
1.下列一定是指数函数的是( )
A.形如y=ax的函数 B.y=xa(a>0,且a≠1)
C.y=(|a|+2)x D.y=(a-2)ax
解析:∵y=(|a|+2)x符合指数函数的定义,
∴y=(|a|+2)x是指数函数.
答案:C2.指数函数y=ax与y=bx的图象如右图1,则( )
A.a<0,b<0
B.a<0,b>0
C.0
D.0
3.函数y=πx的值域是( )
A.(0,+∞) B.[0,+∞)
C.R D.(-∞,0)
答案:A4.函数y=(a-1)x在R上为减函数,则a的取值范围是________.
解析:∵y=(a-1)x在R上递减,
∴0
5.已知指数函数f(x)的图象过点(3,8),求f(6)的值.
解:设f(x)=ax,则a3=8,∴a=2,∴f(x)=2x,∴f(6)=26=64.互 动 课 堂 典 例 导 悟
类型一 指数函数的概念
[例1] 指出下列函数哪些是指数函数:
(1)y=4x;(2)y=x4;(3)y=-4x;(4)y=(-4)x;(5)y=4x2;(6)y=xx;(7)y=(2a-1)x(a>,且a≠1).
[分析] 根据指数函数的定义进行判断.[解] (1)(7)为指数函数.
(2)不是指数函数.
(3)是-1与指数函数4x的乘积,所以不是指数函数.
(4)中底数-4<0,所以不是指数函数.
(5)中指数不是自变量x,所以不是指数函数.
(6)中底数x不是常数,不符合指数函数的定义,所以不是指数函数.变式体验1 若y=(a-3)·(a-2)x是指数函数,求a的值.(2)由图象知函数在(-∞,-1]上是增函数,在[-1,+∞)上是减函数.
(3)由图象知当x=-1时,有最大值1,无最小值.
[点评] (1)指数型函数的作图一般从最基本的指数函数入手,通过平移、伸缩、对称变换得到.(2)带有绝对值的图象作图,一般分为两种情况,一种是去掉绝对值作图,一种是不去绝对值,如y=f(|x|)可依据函数是偶函数,先作出y=f(x)(x≥0)的图象,x<0时的图象只需将y=f(x)(x≥0)图象关于y轴对称过去即可,又如y=|f(x)|的图象,可作出y=f(x)的图象,保留x轴上方图象,将下方图象关于x轴对称过去即可得y=|f(x)|的图象.[点评] 本题中的函数都不是指数函数,但都与指数函数有关.根据指数函数的定义域为R,值域为(0,+∞),结合前一章求函数定义域和值域的方法,可以求解一些简单函数的定义域和值域.在求解中要注意正确运用指数函数的单调性.在求值域问题时,既要考虑指数函数的单调性,还应注意指数函数的值域为(0,+∞).类型四 比较大小
[例4] 比较下列各组数的大小:[分析] 因为是两个指数幂比较大小,故解答本题可利用指数函数的图象与性质或通过寻求第三个数,将两数进行比较.[点评] 比较幂的大小的常用方法:
(1)对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断.(2)对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图象的变化规律来判断.(3)对于底数不同,且指数也不同的幂的大小比较,则应通过中间值来比较.变式体验4 已知a=0.80.7,b=0.80.9,c=1.20.8,则a、b、c的大小关系是( )
A.a>b>c B.b>a>c
C.c>b>a D.c>a>b
解析:∵y=0.8x是减函数,∴a=0.80.7>0.80.9=b,且a=0.80.7<0.80=1.又c=1.20.8>1,∴c>a>b.故选D.
答案:D 思 悟 升 华
1.指数函数是形式化的概念,形如y=ax(a>0,且a≠1)的函数被称为指数函数,这里x是自变量,要判断一个函数是否是指数函数,需抓住三点:①底数大于零且不等于1;②幂指数有单一的自变量x;③系数为1,且没有其他的项.
2.当底数a大小不定时,必须分“a>1”和“0
关于指数型函数y=af(x)+b的定义域可结合求函数定义域的方法,通过解不等式或不等式组来解决;求其值域可采用换元法,既要考虑指数函数的单调性,还应注意指数函数的值域是(0,+∞).5.比较幂值的大小常常化为同底数的幂,根据指数函数的单调性比较大小.如果不能化为同底数的幂,则要借助幂值的范围利用中间值过渡(常选1作中间值).课时作业(15)
