高一数学 2.2.2 对数函数及其性质(2)课件 新人教A版必修1
文档属性
| 名称 | 高一数学 2.2.2 对数函数及其性质(2)课件 新人教A版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 230.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 15:04:22 | ||
图片预览











文档简介
课件35张PPT。2.2 对数函数 2.2.2 对数函数及其性质第2课时
对数函数的性质应用研 习 新 知 新 知 视 界
1.复合函数y=logaf(x),x∈D的单调性:设集合M?D,若a>1,且u=f(x)在x∈M上单调递增(减),集合M对应的区间是函数y=logaf(x)的增(减)区间;若03.(1)对数函数y=logax(a>0,且a≠1)与指数函数y=ax(a>0,且a≠1)互为反函数.
(2)互为反函数的两函数的图象关于直线y=x对称.自 我 检 测
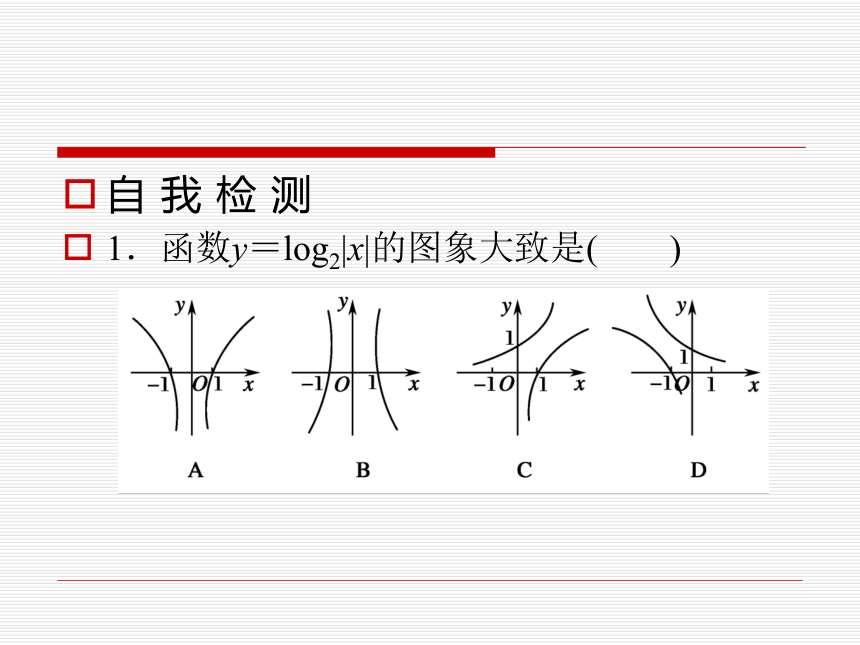
1.函数y=log2|x|的图象大致是( )答案:A答案:D答案:D4.已知logm7解析:∵logm7∴0>log7m>log7n.
∵y=log7x在(0,1)内递增,∴0答案:0①(1)中底数含有参数;
②(2)中底数相同.
解答本题可根据对数函数的单调性转化为一般不等式(组)求解.[点评] (1)解对数不等式问题通常转化为一般不等式(组)求解,其依据是对数函数的单调性.
(2)解决与对数函数相关的问题时要遵循“定义域优先”原则.
(3)若含有字母,应考虑分类讨论.变式体验1 已知loga(2a+1)解:(1)当a>1时,原不等式等价于类型二 对数型函数的单调性问题
[例2] 讨论函数f(x)=loga(3x2-2x-1)的单调性.
[分析] 本题考查复合函数单调性的判定方法.一般地,设函数y=f(u),u=g(x)都是给定区间上的单调函数.
(1)若y=f(u),u=g(x)在给定区间上的单调性相同,则函数y=f[g(x)]是增函数;
(2)若y=f(u),u=g(x)在给定区间上的单调性相反,则函数y=f[g(x)]是减函数.[点评] 要求复合函数的单调区间,首先要搞清函数的复合关系,即把整个函数分解为若干个单调函数,按照“同增异减”的法则去判断函数的单调性.要讨论函数的单调区间,必须在函数的定义域内进行,同时,还要注意区间的端点值.变式体验2 已知y=loga(2-ax)在[0,1]上是关于x的减函数,求a的取值范围.类型三 对数函数的最值问题
[例3] 已知f(x)=2+log3x,x∈[1,3],求y=[f(x)]2+f(x2)的最大值及相应的x的值.
[分析] 先确定y=[f(x)]2+f(x2)的定义域,然后转化成关于log3x的一个一元二次函数,利用一元二次函数求最值.[解] ∵f(x)=2+log3x,x∈[1,3].
∴y=[f(x)]2+f(x2)=(log3x)2+6log3x+6且定义域为[1,3].
令t=log3x(x∈[1,3]).因为t=log3x在[1,3]上是增函数,所以0≤t≤1.
从而要求y=[f(x)]2+f(x2)在[1,3]上的最大值,只需求y=t2+6t+6在[0,1]上的最大值即可.∵y=t2+6t+6在[-3,+∞)上是增函数,
∴当t=1,即x=3时,ymax=1+6+6=13.
综上可知,当x=3时,y=[f(x)]2+f(x2)的最大值为13.
变式体验3 已知集合A={x|2≤x≤π},定义在集合A上的函数y=logax的最大值比最小值大1,求a的值.思 悟 升 华
1.与对数函数有关的复合函数单调区间的求法
求与对数函数有关的复合函数的单调区间,首要的是弄清楚这个函数是怎样复合而成的,再按“同增异减”的方法来求其单调区间.
2.对于对数型复合函数的综合应用的题目,无论是求最值还是求参数的取值范围,必须抓住两点:一是先求出原函数的定义域,二是在定义域内求出函数的单调区间,然后由函数的单调性求出其最值或参数的取值范围.此外在解题过程中一定要注意数形结合方法的灵活应用.课时作业(20)
对数函数的性质应用研 习 新 知 新 知 视 界
1.复合函数y=logaf(x),x∈D的单调性:设集合M?D,若a>1,且u=f(x)在x∈M上单调递增(减),集合M对应的区间是函数y=logaf(x)的增(减)区间;若0
(2)互为反函数的两函数的图象关于直线y=x对称.自 我 检 测
1.函数y=log2|x|的图象大致是( )答案:A答案:D答案:D4.已知logm7
∵y=log7x在(0,1)内递增,∴0
②(2)中底数相同.
解答本题可根据对数函数的单调性转化为一般不等式(组)求解.[点评] (1)解对数不等式问题通常转化为一般不等式(组)求解,其依据是对数函数的单调性.
(2)解决与对数函数相关的问题时要遵循“定义域优先”原则.
(3)若含有字母,应考虑分类讨论.变式体验1 已知loga(2a+1)
[例2] 讨论函数f(x)=loga(3x2-2x-1)的单调性.
[分析] 本题考查复合函数单调性的判定方法.一般地,设函数y=f(u),u=g(x)都是给定区间上的单调函数.
(1)若y=f(u),u=g(x)在给定区间上的单调性相同,则函数y=f[g(x)]是增函数;
(2)若y=f(u),u=g(x)在给定区间上的单调性相反,则函数y=f[g(x)]是减函数.[点评] 要求复合函数的单调区间,首先要搞清函数的复合关系,即把整个函数分解为若干个单调函数,按照“同增异减”的法则去判断函数的单调性.要讨论函数的单调区间,必须在函数的定义域内进行,同时,还要注意区间的端点值.变式体验2 已知y=loga(2-ax)在[0,1]上是关于x的减函数,求a的取值范围.类型三 对数函数的最值问题
[例3] 已知f(x)=2+log3x,x∈[1,3],求y=[f(x)]2+f(x2)的最大值及相应的x的值.
[分析] 先确定y=[f(x)]2+f(x2)的定义域,然后转化成关于log3x的一个一元二次函数,利用一元二次函数求最值.[解] ∵f(x)=2+log3x,x∈[1,3].
∴y=[f(x)]2+f(x2)=(log3x)2+6log3x+6且定义域为[1,3].
令t=log3x(x∈[1,3]).因为t=log3x在[1,3]上是增函数,所以0≤t≤1.
从而要求y=[f(x)]2+f(x2)在[1,3]上的最大值,只需求y=t2+6t+6在[0,1]上的最大值即可.∵y=t2+6t+6在[-3,+∞)上是增函数,
∴当t=1,即x=3时,ymax=1+6+6=13.
综上可知,当x=3时,y=[f(x)]2+f(x2)的最大值为13.
变式体验3 已知集合A={x|2≤x≤π},定义在集合A上的函数y=logax的最大值比最小值大1,求a的值.思 悟 升 华
1.与对数函数有关的复合函数单调区间的求法
求与对数函数有关的复合函数的单调区间,首要的是弄清楚这个函数是怎样复合而成的,再按“同增异减”的方法来求其单调区间.
2.对于对数型复合函数的综合应用的题目,无论是求最值还是求参数的取值范围,必须抓住两点:一是先求出原函数的定义域,二是在定义域内求出函数的单调区间,然后由函数的单调性求出其最值或参数的取值范围.此外在解题过程中一定要注意数形结合方法的灵活应用.课时作业(20)
