12.4 综合与实践一次函数模型的应用 课件(共25张PPT)
文档属性
| 名称 | 12.4 综合与实践一次函数模型的应用 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 08:23:06 | ||
图片预览




文档简介
(共25张PPT)
沪科版 八年级上册
12.4 综合与实践
一次函数模型的应用
教学目标:
1.会结合实际问题建立一次函数模型,知道
函数建模的一般步骤和方法.
2.应用函数模型解决简单的实际问题.
3.学会分析问题、解决问题的一般方法.
教学重点:
会结合实际问题建立一次函数模型,知道函数建模的一般步骤和方法.
教学难点:
应用函数模型解决简单的实际问题.
O
x
y
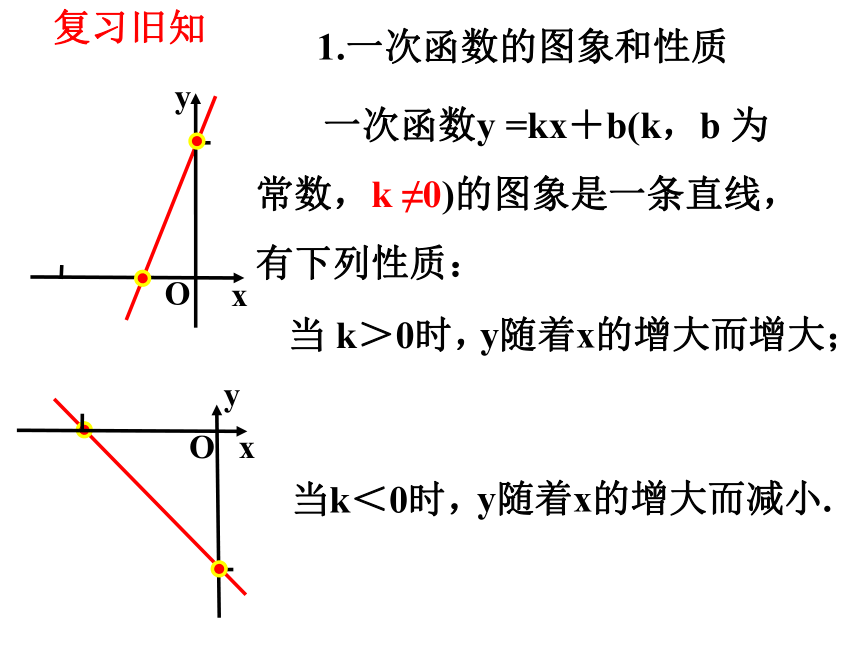
y随着x的增大而减小.
当k<0时,
O
x
y
y随着x的增大而增大;
当 k>0时,
一次函数y =kx+b(k,b 为常数,k ≠0)的图象是一条直线,有下列性质:
复习旧知
1.一次函数的图象和性质
用待定系数法求一次函数解析式一般步骤:
(1)先设出一次函数解析式为y=kx+b;
(2)将已知两点的坐标代入所设的解析式,建立
一个以k 、b为未知数的 二元一次方程组;
(3) 解二元一次方程组,求出k、b的值;
(4)将求出的k、b的值代入所设的解析式,
写出具体的一次函数解析式.
2.求一次函数的解析式的一般方法
复习旧知
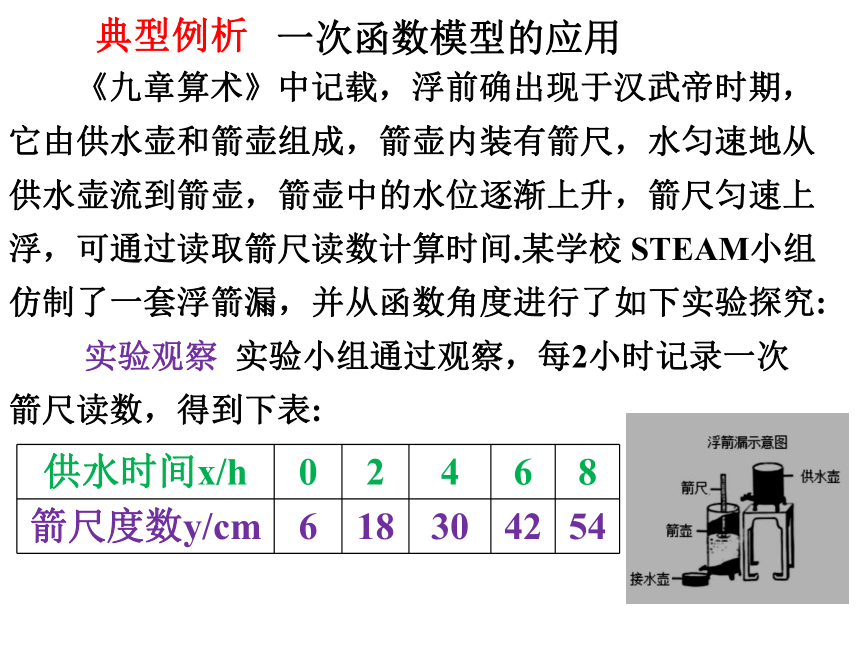
《九章算术》中记载,浮前确出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间.某学校 STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
实验观察 实验小组通过观察,每2小时记录一次箭尺读数,得到下表:
典型例析
一次函数模型的应用
供水时间x/h 0 2 4 6 8
箭尺度数y/cm 6 18 30 42 54
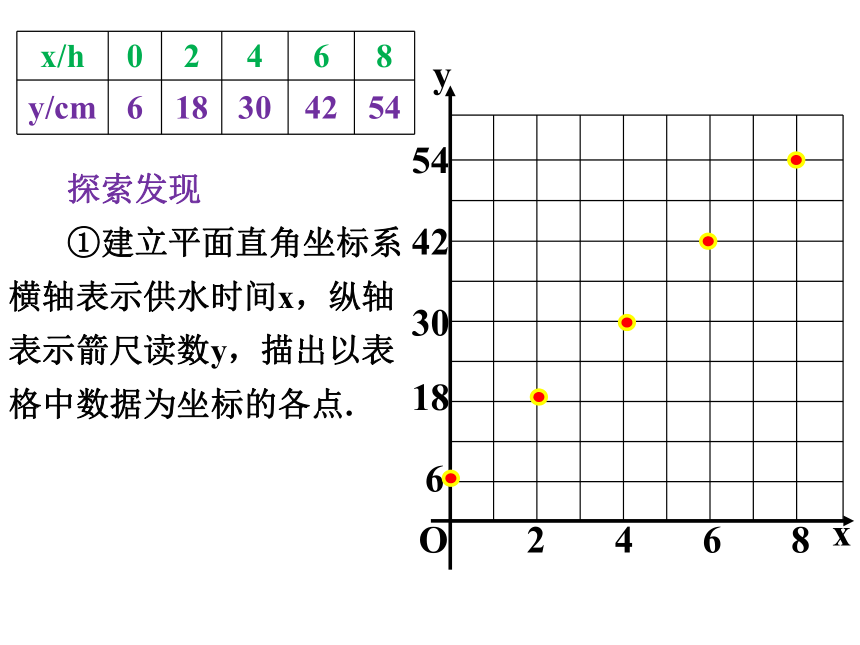
探索发现
①建立平面直角坐标系横轴表示供水时间x,纵轴表示箭尺读数y,描出以表格中数据为坐标的各点.
②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
结论应用
应用上述发现的规律估算:
①供水时间达到12小时时,箭尺的读数为多少cm
②如果本次实验记录的开始时间是上午8:00,那么当箭尺读数为90cm时是几点钟 (箭尺最大读数为100cm)
探索发现
①建立平面直角坐标系横轴表示供水时间x,纵轴表示箭尺读数y,描出以表格中数据为坐标的各点.
y
O
x
2
4
6
6
18
30
8
42
54
x/h 0 2 4 6 8
y/cm 6 18 30 42 54
探索发现
y
O
x
2
4
6
6
18
30
8
42
54
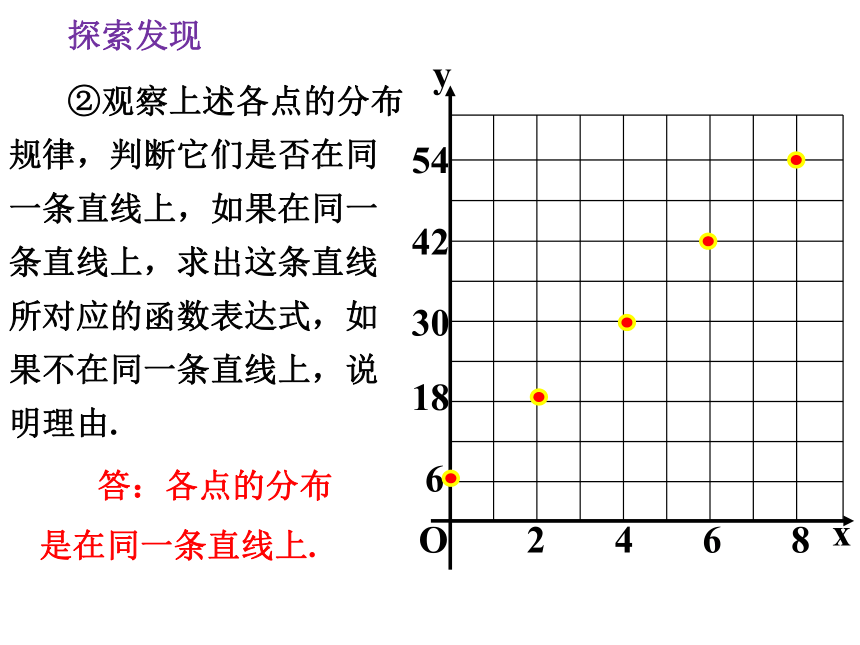
②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
答:各点的分布是在同一条直线上.
y
O
x
2
4
6
6
18
30
8
42
54
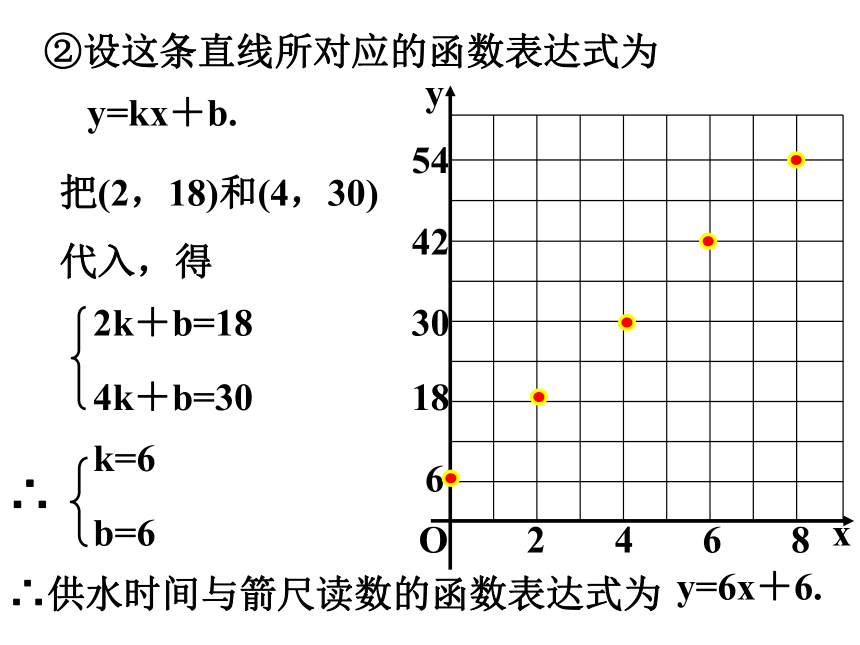
②设这条直线所对应的函数表达式为
y=kx+b.
y=6x+6.
2k+b=18
4k+b=30
∴
k=6
b=6
∴供水时间与箭尺读数的函数表达式为
把(2,18)和(4,30)
代入,得
结论应用
应用上述发现的规律估算:
①供水时间达到12小时时,箭尺的读数为多少cm
②如果本次实验记录的开始时间是上午8:00,那么当
箭尺读数为90cm时是几点钟 (箭尺最大读数为100cm)
①供水时间达到12小时时,箭尺的读数为
y=6×12 + 6
=78(cm)
②当箭尺读数为90cm时,有
90=6x+6,
∴x=14.
∵本次实验记录的开始时间是上午8:00,
∴箭尺读数为90cm时是
8:00+14:00=22:00.
例 今年4月初,某地连续降雨,导致该地某水库水位持上涨,下表是该水库4月1日~4月 4 日的水位变化情况:
(1)请建立该水库水位y 与日期x 之间的函数模型;(2)请用求出的函数表达式预测该水库今年 4月
6日的水位;
(3)能用求出的函数表达式预测该水库今年12月
1日的位吗?
日期x 1 2 3 4
水位ym 20.00 20.50 21.00 21.50
由表可知,水库的水位y随日期 x的变化是均匀的,
解:(1)
y=0.5x+19.5.
20k+b=15
36k+b=23
②
①
∴
k=0.5
b=19.5
∴水位y与日期 x的函数表达式为
所以y与x之间为一次函数关系,
设 y=kx+b.
把(1,20.00)和(2,20.50)代入,得
(2)当x=6时,
(3)不能.
y=0.5×6+19.5
=22.5
因为12月远离4月,
所建立的函数模型
远离已知数据,
这样做预测是不可靠的.
函数建模过程一般步骤
函数模型的建立建立两个变量之间的函数模型可以通过以下几个步骤来完成:
(1)建立适当的平面直角坐标系,以问题中自变量的值为横坐标,对应的函数值为纵坐标,在平面直角坐标系内描出相应的点若干个.
(2)观察描出的点在平面直角坐标系内的分布情况,从而推测函数图象的大致形状,结合已学函数知识进一步猜想y与工之间的函数关系的类型.
(3)根据猜想及已知条件,用待定系数法求出函数表达式并检验必要时可对所求表达式作适当修正.
(4)运用求得的函数表达式解决相关问题.
1.潜水员在深海中潜水时所受的水压随着潜水深度的增加
而增加.现将经过5次测量,得到观察值如 下表:
水深d/m 0 10 25 40 55 75
水压p/Pa 0 0.9 ×105 2.2 ×105 3.5 ×105 4.9 ×105 6.6
×105
(1)在平面直角坐标系内,描出各组有序数对(d,p)
所对应的点;
(2)水压p与水深d间的关系,可用哪种函数关系去模拟?
(3)如果一名潜水员所承受的最大水压为 7.8×105 Pa,试问他能否在水下90m处作业
练习巩固
p
O
d
20
40
60
1×105
3×105
6×105
80
(1)在平面直角坐标系内,描出各组有序数对
(d,p)所对应的点;
解:
p
O
d
20
40
60
1×105
3×105
6×105
80
(2)图象似一条直线,
∴水压p与水深d间的关系
可用一次函数关系去模拟.
设p=dx+b.
水深d/m 0 10 25 40 55 75
水压p/Pa 0 0.9 ×105 2.2 ×105 3.5 ×105 4.9 ×105 6.6
×105
(3)
10k+b=0.9×105
b=0
②
①
∴
k=0.9×104
b=0
∵
p=0.9×104d.
∴水压p与水深d函数表达式为
7.8×105=0.9×104d
当p=7.8×105时,得
∴x≈87(m)
答:他不能在水下90m处作业.
<90m
2.小明练习 100 米短跑,训练时间与 100 米短记录如下:
(1)请你为小明的100米短跑成绩 y(秒)与训练时间x(月)
的关系建立函数模型;
(2)用所求出的函数解析式预测小明训练 6个月的100米
短跑成绩;
(3)能用所求出的函数解析式预测小明训练 3 年的100米
短跑成绩吗 为什么
时间x(月) 1 2 3 4
成绩y(秒) 15.6 15.4 15.2 15.0
由表可知,短跑成绩y随训练时间 x的变化是均匀的,
解:(1)
y= -0.2x+15.8.
k+b=15.6
2k+b=15.4
∴
k=-0.2
b=15.8
∴成绩y与时间x的函数表达式为
所以y与x之间为一次函数关系,
设 y=kx+b.
把(1,15.6)和(2,15.4)代入,得
(2)当x=6时,
(3)不能.
y=-0.2×6+15.8
=14.6
因为短跑的成绩在短时间内可这样
但不会永远提高,
这样做预测是不可靠的.
∴预测小明训练 6个月的100米 短跑成绩为14.6秒
提高,
3.已知部分鞋子的型号“码”数与鞋子长度“cm”之间存在一种换算关系如下:
(1)通过画图、观察,猜想这种换算规律可能用哪种函数关系去模拟?
(2)设鞋子的“码”数为x,长度为ycm,试写出y与x之间的函数表达式;
(3)小明量了一下自己所穿鞋长是24.5cm,那么他穿多大码的鞋?
型号/码 20 36 42
长度/cm 15 23 26
y
O
x
20
40
60
30
15
(1)在平面直角坐标系内,描出“码”数x
与长度y有序数对 (x,y)所对应的点;
型号/码 长度/cm
20 15
36 23
42 26
图象似一条直线,可猜想“码”数与长度或存在一次函数关系.
解:
y=0.5x+5.
(2)
20k+b=15
36k+b=23
②
①
∴
k=0.5
b=5
∴ “码”数与长度函数表达式为
24.5=0.5x+5.
(3)
当y=24.5时,得
∴x=39
答:小明穿39码的鞋.
图象似一条直线,可猜想“码”数与长度或存在一次函数关系.
设 y=kx+b.
把(20,15)和(36,23)代入,得
(1)如何获取数据?
(2)如何处理获取的数据并建模?
(3)你选取函数模型的依据是什么?
课堂小结
(4)运用一次函数解决实际问题的方法和步骤:
①首先判断问题中的两个变量之间是否满足一次函数关系;
②当确定两个变量是一次函数关系时,就可以求出其函数表达式;
③运用一次函数的图象和性质解决问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
12.4 综合与实践
一次函数模型的应用
教学目标:
1.会结合实际问题建立一次函数模型,知道
函数建模的一般步骤和方法.
2.应用函数模型解决简单的实际问题.
3.学会分析问题、解决问题的一般方法.
教学重点:
会结合实际问题建立一次函数模型,知道函数建模的一般步骤和方法.
教学难点:
应用函数模型解决简单的实际问题.
O
x
y
y随着x的增大而减小.
当k<0时,
O
x
y
y随着x的增大而增大;
当 k>0时,
一次函数y =kx+b(k,b 为常数,k ≠0)的图象是一条直线,有下列性质:
复习旧知
1.一次函数的图象和性质
用待定系数法求一次函数解析式一般步骤:
(1)先设出一次函数解析式为y=kx+b;
(2)将已知两点的坐标代入所设的解析式,建立
一个以k 、b为未知数的 二元一次方程组;
(3) 解二元一次方程组,求出k、b的值;
(4)将求出的k、b的值代入所设的解析式,
写出具体的一次函数解析式.
2.求一次函数的解析式的一般方法
复习旧知
《九章算术》中记载,浮前确出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间.某学校 STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
实验观察 实验小组通过观察,每2小时记录一次箭尺读数,得到下表:
典型例析
一次函数模型的应用
供水时间x/h 0 2 4 6 8
箭尺度数y/cm 6 18 30 42 54
探索发现
①建立平面直角坐标系横轴表示供水时间x,纵轴表示箭尺读数y,描出以表格中数据为坐标的各点.
②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
结论应用
应用上述发现的规律估算:
①供水时间达到12小时时,箭尺的读数为多少cm
②如果本次实验记录的开始时间是上午8:00,那么当箭尺读数为90cm时是几点钟 (箭尺最大读数为100cm)
探索发现
①建立平面直角坐标系横轴表示供水时间x,纵轴表示箭尺读数y,描出以表格中数据为坐标的各点.
y
O
x
2
4
6
6
18
30
8
42
54
x/h 0 2 4 6 8
y/cm 6 18 30 42 54
探索发现
y
O
x
2
4
6
6
18
30
8
42
54
②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
答:各点的分布是在同一条直线上.
y
O
x
2
4
6
6
18
30
8
42
54
②设这条直线所对应的函数表达式为
y=kx+b.
y=6x+6.
2k+b=18
4k+b=30
∴
k=6
b=6
∴供水时间与箭尺读数的函数表达式为
把(2,18)和(4,30)
代入,得
结论应用
应用上述发现的规律估算:
①供水时间达到12小时时,箭尺的读数为多少cm
②如果本次实验记录的开始时间是上午8:00,那么当
箭尺读数为90cm时是几点钟 (箭尺最大读数为100cm)
①供水时间达到12小时时,箭尺的读数为
y=6×12 + 6
=78(cm)
②当箭尺读数为90cm时,有
90=6x+6,
∴x=14.
∵本次实验记录的开始时间是上午8:00,
∴箭尺读数为90cm时是
8:00+14:00=22:00.
例 今年4月初,某地连续降雨,导致该地某水库水位持上涨,下表是该水库4月1日~4月 4 日的水位变化情况:
(1)请建立该水库水位y 与日期x 之间的函数模型;(2)请用求出的函数表达式预测该水库今年 4月
6日的水位;
(3)能用求出的函数表达式预测该水库今年12月
1日的位吗?
日期x 1 2 3 4
水位ym 20.00 20.50 21.00 21.50
由表可知,水库的水位y随日期 x的变化是均匀的,
解:(1)
y=0.5x+19.5.
20k+b=15
36k+b=23
②
①
∴
k=0.5
b=19.5
∴水位y与日期 x的函数表达式为
所以y与x之间为一次函数关系,
设 y=kx+b.
把(1,20.00)和(2,20.50)代入,得
(2)当x=6时,
(3)不能.
y=0.5×6+19.5
=22.5
因为12月远离4月,
所建立的函数模型
远离已知数据,
这样做预测是不可靠的.
函数建模过程一般步骤
函数模型的建立建立两个变量之间的函数模型可以通过以下几个步骤来完成:
(1)建立适当的平面直角坐标系,以问题中自变量的值为横坐标,对应的函数值为纵坐标,在平面直角坐标系内描出相应的点若干个.
(2)观察描出的点在平面直角坐标系内的分布情况,从而推测函数图象的大致形状,结合已学函数知识进一步猜想y与工之间的函数关系的类型.
(3)根据猜想及已知条件,用待定系数法求出函数表达式并检验必要时可对所求表达式作适当修正.
(4)运用求得的函数表达式解决相关问题.
1.潜水员在深海中潜水时所受的水压随着潜水深度的增加
而增加.现将经过5次测量,得到观察值如 下表:
水深d/m 0 10 25 40 55 75
水压p/Pa 0 0.9 ×105 2.2 ×105 3.5 ×105 4.9 ×105 6.6
×105
(1)在平面直角坐标系内,描出各组有序数对(d,p)
所对应的点;
(2)水压p与水深d间的关系,可用哪种函数关系去模拟?
(3)如果一名潜水员所承受的最大水压为 7.8×105 Pa,试问他能否在水下90m处作业
练习巩固
p
O
d
20
40
60
1×105
3×105
6×105
80
(1)在平面直角坐标系内,描出各组有序数对
(d,p)所对应的点;
解:
p
O
d
20
40
60
1×105
3×105
6×105
80
(2)图象似一条直线,
∴水压p与水深d间的关系
可用一次函数关系去模拟.
设p=dx+b.
水深d/m 0 10 25 40 55 75
水压p/Pa 0 0.9 ×105 2.2 ×105 3.5 ×105 4.9 ×105 6.6
×105
(3)
10k+b=0.9×105
b=0
②
①
∴
k=0.9×104
b=0
∵
p=0.9×104d.
∴水压p与水深d函数表达式为
7.8×105=0.9×104d
当p=7.8×105时,得
∴x≈87(m)
答:他不能在水下90m处作业.
<90m
2.小明练习 100 米短跑,训练时间与 100 米短记录如下:
(1)请你为小明的100米短跑成绩 y(秒)与训练时间x(月)
的关系建立函数模型;
(2)用所求出的函数解析式预测小明训练 6个月的100米
短跑成绩;
(3)能用所求出的函数解析式预测小明训练 3 年的100米
短跑成绩吗 为什么
时间x(月) 1 2 3 4
成绩y(秒) 15.6 15.4 15.2 15.0
由表可知,短跑成绩y随训练时间 x的变化是均匀的,
解:(1)
y= -0.2x+15.8.
k+b=15.6
2k+b=15.4
∴
k=-0.2
b=15.8
∴成绩y与时间x的函数表达式为
所以y与x之间为一次函数关系,
设 y=kx+b.
把(1,15.6)和(2,15.4)代入,得
(2)当x=6时,
(3)不能.
y=-0.2×6+15.8
=14.6
因为短跑的成绩在短时间内可这样
但不会永远提高,
这样做预测是不可靠的.
∴预测小明训练 6个月的100米 短跑成绩为14.6秒
提高,
3.已知部分鞋子的型号“码”数与鞋子长度“cm”之间存在一种换算关系如下:
(1)通过画图、观察,猜想这种换算规律可能用哪种函数关系去模拟?
(2)设鞋子的“码”数为x,长度为ycm,试写出y与x之间的函数表达式;
(3)小明量了一下自己所穿鞋长是24.5cm,那么他穿多大码的鞋?
型号/码 20 36 42
长度/cm 15 23 26
y
O
x
20
40
60
30
15
(1)在平面直角坐标系内,描出“码”数x
与长度y有序数对 (x,y)所对应的点;
型号/码 长度/cm
20 15
36 23
42 26
图象似一条直线,可猜想“码”数与长度或存在一次函数关系.
解:
y=0.5x+5.
(2)
20k+b=15
36k+b=23
②
①
∴
k=0.5
b=5
∴ “码”数与长度函数表达式为
24.5=0.5x+5.
(3)
当y=24.5时,得
∴x=39
答:小明穿39码的鞋.
图象似一条直线,可猜想“码”数与长度或存在一次函数关系.
设 y=kx+b.
把(20,15)和(36,23)代入,得
(1)如何获取数据?
(2)如何处理获取的数据并建模?
(3)你选取函数模型的依据是什么?
课堂小结
(4)运用一次函数解决实际问题的方法和步骤:
①首先判断问题中的两个变量之间是否满足一次函数关系;
②当确定两个变量是一次函数关系时,就可以求出其函数表达式;
③运用一次函数的图象和性质解决问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
