安徽省合肥市第四十八中学2022-2023学年八年级上学期期中考试数学试卷(图片版 含答案)
文档属性
| 名称 | 安徽省合肥市第四十八中学2022-2023学年八年级上学期期中考试数学试卷(图片版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 10:30:25 | ||
图片预览




文档简介
八年级数学阶段练习参考答案
一、选择题:1-5 ACDCB; 6-10 DBDCC
二、填空题:11、-1;12、100°;13、7;14、(2,3);3
15.解: (1)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a﹣2=1,且2a+8≠5,
解得:a=3,故2a+8=14,
则P(1,14);.......4分
(2)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
当a=﹣10时,a﹣2=﹣12,2a+8=﹣12,则P(﹣12,﹣12);
当a=﹣2时,a﹣2=﹣4,2a+8=4,则P(﹣4,4).
综上:P(﹣12,﹣12)或(﹣4,4)........8分
16.解:(1)设y﹣2=k(x+4),
将x=2、y=5代入,得:6k=3,解得k=,
∴y﹣2=(x+4),即 .......4分
(2)将点M(a,﹣3)代入 ,得:
解得:a=﹣14 .......8分
17.解:(1)如图所示:.......2分
(2)S△ABC=3×4﹣×2×3﹣×1×2﹣×2×4=4, .......5分
(3)如图所示:.......8分
18.证明:∵AB=AC,BD=CE,
∴AB﹣BD=AC﹣CE,即AD=AE,
在△ACD和△ABE中,
∵
∴△ACD≌△ABE(SAS).
∴∠B=∠C........8分
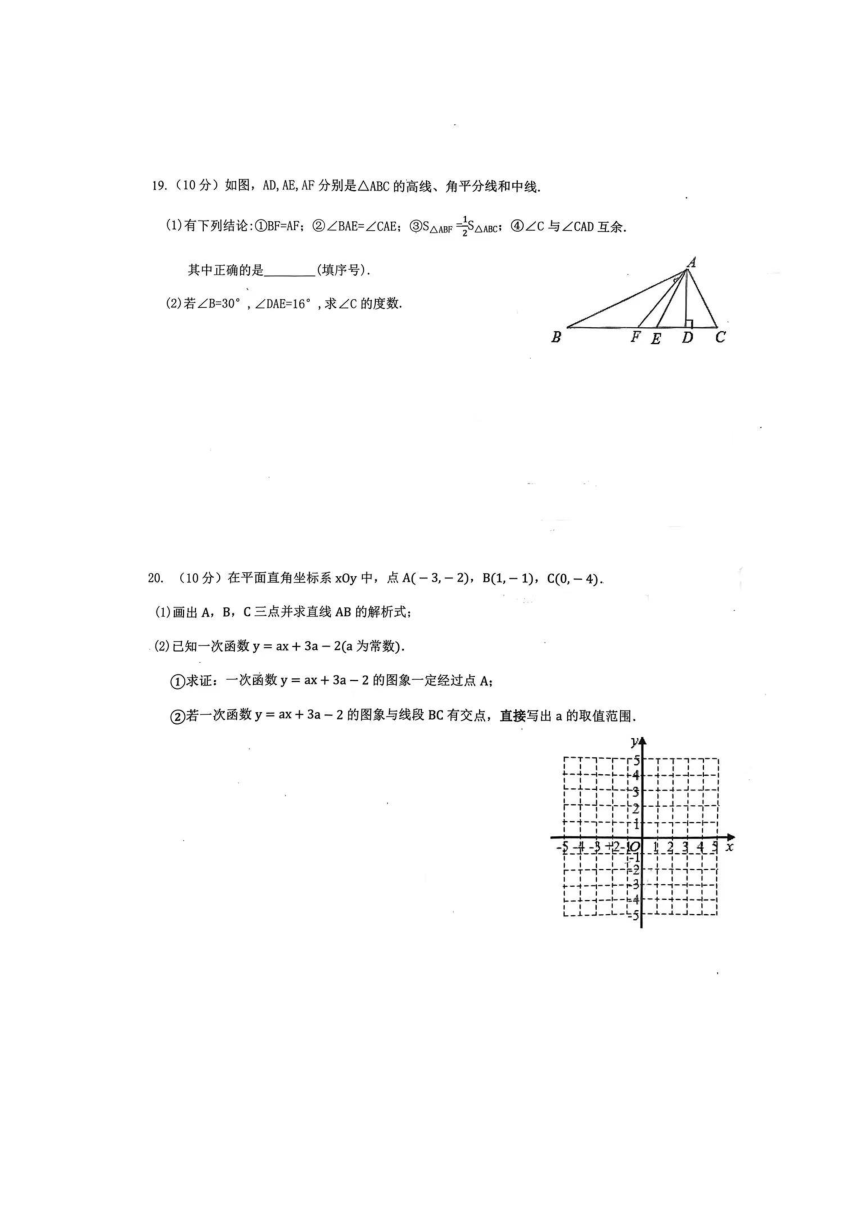
19.解:(1) ∵AD,AE,AF分别是△ABC的高线,角平分线和中线,
∴BF=FC,故①错误;
∴∠BAE=∠CAE,故②正确;
∴S△ABF=S△ABC,故③正确;
∴∠C与∠CAD互余,故④正确;
故答案为②③④;.......4分
(2)∵AD,AE,AF分别是△ABC的高线,角平分线和中线,
∴∠ADE=90°,∴∠AED=180°﹣90°﹣16°=74°,
∵∠B=30°,∴∠BAE=∠AED﹣∠B=74°﹣30°=44°
∵AE是△ABC的角平分线
∴∠BAC=2∠BAE= 88°
在△ABC中 ∠C=180°-(∠B+∠BAC)=62°........10分
20.解:(1)如图,设过AB的直线的解析式为y=kx+b,
把A(﹣3,﹣2),B(1,﹣1)代入得,
解得,
∴直线AB的解析式为y=x﹣;.......4分
(2)①证明:把x=﹣3代入y=ax+3a﹣2得,y=﹣2
∴ 图象必经过点A(-3,-2);.......7分
②一次函数y=ax+3a﹣2的图象与线段BC有交点,
把B(1,﹣1)代入直线得:﹣1=a+3a﹣2,∴a=,
把C(0,﹣4)代入直线得:﹣4=3a﹣2, ∴a=﹣,
当a=0时,y=ax+3a﹣2不是一次函数,
综上:a的取值范围为﹣≤a≤且a≠0........10分
21.解:(1)设大货车x辆,则小货车有(20﹣x)辆,
15x+10(20﹣x)=240,
解得:x=8,20﹣x=20﹣8=12(辆),
答:大货车用8辆.小货车用12辆;.......3分
(2)①由题意得:15x+10(10﹣x)≥130,
解得:x≥6,
∵ 大车共有8辆,
∴ 6≤x≤8且x为整数;.......6分
②设总运费为W元,
∵调往A地的大车有x辆,则到A地的小车有(10﹣x)辆,
∴到B的大车(8﹣x)辆,到B的小车有[12﹣(10﹣x)]=(2+x)辆,
则 W=630x+420(10﹣x)+750(8﹣x)+550(2+x)
=630x+4200﹣420x+6000﹣750x+1100+550x
=10x+11300........9分
∵ W随x的增大而增大;
又∵6≤x≤8且为整数;
∴当x=6时,w有最小值,W最小=10×6+11300=11360元.
答:分别安排去A地、B地的大车6辆、2辆,再安排去A地、B地的小车4辆、8辆,最少费用为11360元........12分
22.(1)证明:∵AE、BD是△ABM的高,
∴∠ADB=∠AEB=∠AEM=90°,
∵∠ACD=∠ECB,
∠MAE+∠ADC+∠ACD=180°,∠CBE+∠ECB+∠CEB=180°,
∴∠MAE=∠CBE,
在△AME和△BCE中,,
∴△AME≌△BCE(ASA)........4分
(2)证明:∵BD平分∠ABM,BD是高,
∴∠ABD=∠MBD,∠ADB=∠MDB=90°,
在△ABD和△MBD中,
,
∴△ABD≌△MBD(ASA),
∴,
∵△AME≌△BCE,
∴AM=BC,即BC=2AD;.......8分
(3)解:过点E作EF⊥ED交BC于点F,
∵∠DEF=∠AEB,
∴∠DEA=∠BEF,
在△AED与△BEF中,
,
∴△AED≌△BEF(ASA),
∴ED=EF,
∴∠EDF=∠EFD=45°,
∵∠BDE=90°,
∴∠MDE=45°........12分
23.解:(1), 乙出发1.5小时后甲先到达终点,此时两人相距10千米........4分
(2)设函数表达式为:S甲=kx+b
把(0.5,0),(1.5,25)代入得
0.5k+b=0 解得: k=25
1.5k+b=25 b=-12.5
∴ S甲=25x-12.5(0.5≤x≤2.5).......10分
(3)如图所示:
.......14分
一、选择题:1-5 ACDCB; 6-10 DBDCC
二、填空题:11、-1;12、100°;13、7;14、(2,3);3
15.解: (1)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a﹣2=1,且2a+8≠5,
解得:a=3,故2a+8=14,
则P(1,14);.......4分
(2)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
当a=﹣10时,a﹣2=﹣12,2a+8=﹣12,则P(﹣12,﹣12);
当a=﹣2时,a﹣2=﹣4,2a+8=4,则P(﹣4,4).
综上:P(﹣12,﹣12)或(﹣4,4)........8分
16.解:(1)设y﹣2=k(x+4),
将x=2、y=5代入,得:6k=3,解得k=,
∴y﹣2=(x+4),即 .......4分
(2)将点M(a,﹣3)代入 ,得:
解得:a=﹣14 .......8分
17.解:(1)如图所示:.......2分
(2)S△ABC=3×4﹣×2×3﹣×1×2﹣×2×4=4, .......5分
(3)如图所示:.......8分
18.证明:∵AB=AC,BD=CE,
∴AB﹣BD=AC﹣CE,即AD=AE,
在△ACD和△ABE中,
∵
∴△ACD≌△ABE(SAS).
∴∠B=∠C........8分
19.解:(1) ∵AD,AE,AF分别是△ABC的高线,角平分线和中线,
∴BF=FC,故①错误;
∴∠BAE=∠CAE,故②正确;
∴S△ABF=S△ABC,故③正确;
∴∠C与∠CAD互余,故④正确;
故答案为②③④;.......4分
(2)∵AD,AE,AF分别是△ABC的高线,角平分线和中线,
∴∠ADE=90°,∴∠AED=180°﹣90°﹣16°=74°,
∵∠B=30°,∴∠BAE=∠AED﹣∠B=74°﹣30°=44°
∵AE是△ABC的角平分线
∴∠BAC=2∠BAE= 88°
在△ABC中 ∠C=180°-(∠B+∠BAC)=62°........10分
20.解:(1)如图,设过AB的直线的解析式为y=kx+b,
把A(﹣3,﹣2),B(1,﹣1)代入得,
解得,
∴直线AB的解析式为y=x﹣;.......4分
(2)①证明:把x=﹣3代入y=ax+3a﹣2得,y=﹣2
∴ 图象必经过点A(-3,-2);.......7分
②一次函数y=ax+3a﹣2的图象与线段BC有交点,
把B(1,﹣1)代入直线得:﹣1=a+3a﹣2,∴a=,
把C(0,﹣4)代入直线得:﹣4=3a﹣2, ∴a=﹣,
当a=0时,y=ax+3a﹣2不是一次函数,
综上:a的取值范围为﹣≤a≤且a≠0........10分
21.解:(1)设大货车x辆,则小货车有(20﹣x)辆,
15x+10(20﹣x)=240,
解得:x=8,20﹣x=20﹣8=12(辆),
答:大货车用8辆.小货车用12辆;.......3分
(2)①由题意得:15x+10(10﹣x)≥130,
解得:x≥6,
∵ 大车共有8辆,
∴ 6≤x≤8且x为整数;.......6分
②设总运费为W元,
∵调往A地的大车有x辆,则到A地的小车有(10﹣x)辆,
∴到B的大车(8﹣x)辆,到B的小车有[12﹣(10﹣x)]=(2+x)辆,
则 W=630x+420(10﹣x)+750(8﹣x)+550(2+x)
=630x+4200﹣420x+6000﹣750x+1100+550x
=10x+11300........9分
∵ W随x的增大而增大;
又∵6≤x≤8且为整数;
∴当x=6时,w有最小值,W最小=10×6+11300=11360元.
答:分别安排去A地、B地的大车6辆、2辆,再安排去A地、B地的小车4辆、8辆,最少费用为11360元........12分
22.(1)证明:∵AE、BD是△ABM的高,
∴∠ADB=∠AEB=∠AEM=90°,
∵∠ACD=∠ECB,
∠MAE+∠ADC+∠ACD=180°,∠CBE+∠ECB+∠CEB=180°,
∴∠MAE=∠CBE,
在△AME和△BCE中,,
∴△AME≌△BCE(ASA)........4分
(2)证明:∵BD平分∠ABM,BD是高,
∴∠ABD=∠MBD,∠ADB=∠MDB=90°,
在△ABD和△MBD中,
,
∴△ABD≌△MBD(ASA),
∴,
∵△AME≌△BCE,
∴AM=BC,即BC=2AD;.......8分
(3)解:过点E作EF⊥ED交BC于点F,
∵∠DEF=∠AEB,
∴∠DEA=∠BEF,
在△AED与△BEF中,
,
∴△AED≌△BEF(ASA),
∴ED=EF,
∴∠EDF=∠EFD=45°,
∵∠BDE=90°,
∴∠MDE=45°........12分
23.解:(1), 乙出发1.5小时后甲先到达终点,此时两人相距10千米........4分
(2)设函数表达式为:S甲=kx+b
把(0.5,0),(1.5,25)代入得
0.5k+b=0 解得: k=25
1.5k+b=25 b=-12.5
∴ S甲=25x-12.5(0.5≤x≤2.5).......10分
(3)如图所示:
.......14分
同课章节目录
