高一数学 2.3.2 平面与平面垂直的判定课件 新人教A版必修2
文档属性
| 名称 | 高一数学 2.3.2 平面与平面垂直的判定课件 新人教A版必修2 |

|
|
| 格式 | zip | ||
| 文件大小 | 236.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 00:00:00 | ||
图片预览






文档简介
课件18张PPT。2.3.2 平面与平面垂直的判定1.已知直线 a∥平面α,a⊥平面β,则()AA.α⊥β
C.α与β不垂直B.α∥β
D.以上都有可能2.已知 PA ⊥矩形 ABCD 所在的平面(如图 1).图中互相垂直的平面有()图 1A.1 对B.2 对C.3 对D.5 对 解析:面 PAD⊥面 AC,面 PAB⊥面
AC,面PAB⊥面PBC,面PDC⊥面PAD,
面PAD⊥面PAB.DA4.已知 O 是△ABC 的外心,P 是平面 ABC 外的一点,且PA =PB=PC,α是经过 PO 的任意一个平面,则()A A.α⊥平面 ABC
B.α与平面 ABC 不垂直
C.α与平面 ABC 可能垂直也可能不垂直
D.以上都不对 解析:由 O 是△ABC 的外心,PA =PB=PC 可得,PO⊥平
面 ABC,∴α⊥平面 ABC.重点二面角的概念及面面垂直的判定 1.二面角的定义:从一条直线出发的两个半平面所组成的
图形叫二面角.这条直线叫做二面角的棱,这两个半平面叫做
二面角的面.记作二面角α-AB-β(简记为 P-AB-Q).
2.二面角的平面角:在二面角α-l-β的棱 l 上任取一点
O,以点 O 为垂足,在半平面α,β内分别作垂直于棱 l 的射线
OA和 OB,则射线 OA 和 OB 构成的∠AOB 叫做二面角的平面角.
二面角的范围:0°≤θ≤180°. 3.面面垂直的定义:两个平面相交,如果它们所成的二面
角是直二面角,就说这两个平面互相垂直.记作α⊥β.
4.面面垂直的判定定理:一个平面过另一个平面的垂线,
则这两个平面垂直(线面垂直→面面垂直).难点求二面角的平面角 要求二面角的平面角,关键是根据图形自身特点找出二面
角的平面角,主要方法有:定义法,垂面法,三垂线定理法.
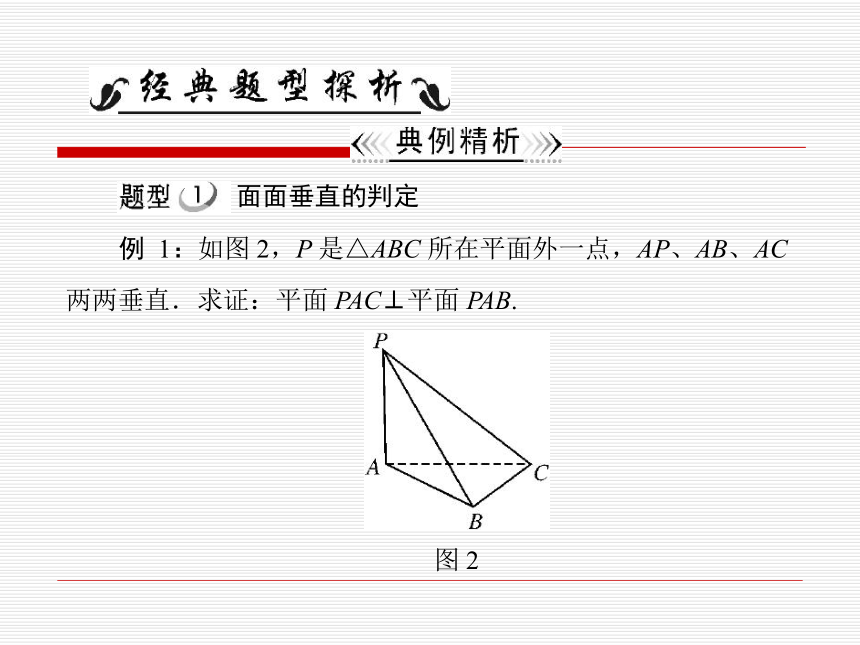
步骤为作,证,求.面面垂直的判定例 1:如图 2,P 是△ABC 所在平面外一点,AP、AB、AC两两垂直.求证:平面 PAC⊥平面 PAB.图 21-1.已知直线 m、n 和平面α、β,下列四个命题中,正确的是()DA.若 m∥α,n∥α,则 m∥n
B.若 m?α,n?α,m∥β,n∥β,则α∥β
C.若α⊥β,m?α,则 m⊥β
D.若α⊥β,m⊥β,m?α,则 m∥α用定义求二面角的平面角的大小面 ABD 与平面 BCD 所成的二面角的大小.图 32-1.下列说法正确的是()DA.二面角的大小范围是大于 0°且小于 90°
B.一个二面角的平面角可以不相等
C.二面角的平面角的顶点可以不在棱上
D.二面角的棱和二面角的平面角所在的平面垂直
A()A.60°B.90°C.45°D.120°
2-2.在正三角形 ABC 中,AD⊥BC 于 D,沿 AD 折成二面 图 4在证明线面平行时,利用中位线的性质证明线线平行,从而得出线面平行,是立体几何中常用的证明方法.3-1.如图 5,已知四边形 ABCD 为矩形,PA ⊥平面 ABCD,M、N、E 分别是 AB、PC、CD 的中点.(1)求证:MN∥平面 PAD;(2)当 MN⊥平面 PCD 时,求二面角 P—CD—B 的大小.图 5 ∴AQ⊥平面 PDC,∴AQ⊥PD.
∵Q 为 PD 的中点,
∴△PAD 为等腰直角三角形,
∴∠PDA=45°,即二面角 P-CD-B 的大小为 45°.错因剖析:考虑不全面,作图可知有两种情况.
正解:D4-1.下列命题中,假命题的个数为()B ①与三角形两边平行的平面平行于这个三角形的第三边;
②与三角形两边垂直的直线垂直于第三边;③与三角形三顶点
等距离的平面平行于这个三角形所在平面.A.0B.1C.2D.3 解析:③是假命题,如果三个顶点不在平面的同侧,则该
平面与三角形所在的平面相交.
C.α与β不垂直B.α∥β
D.以上都有可能2.已知 PA ⊥矩形 ABCD 所在的平面(如图 1).图中互相垂直的平面有()图 1A.1 对B.2 对C.3 对D.5 对 解析:面 PAD⊥面 AC,面 PAB⊥面
AC,面PAB⊥面PBC,面PDC⊥面PAD,
面PAD⊥面PAB.DA4.已知 O 是△ABC 的外心,P 是平面 ABC 外的一点,且PA =PB=PC,α是经过 PO 的任意一个平面,则()A A.α⊥平面 ABC
B.α与平面 ABC 不垂直
C.α与平面 ABC 可能垂直也可能不垂直
D.以上都不对 解析:由 O 是△ABC 的外心,PA =PB=PC 可得,PO⊥平
面 ABC,∴α⊥平面 ABC.重点二面角的概念及面面垂直的判定 1.二面角的定义:从一条直线出发的两个半平面所组成的
图形叫二面角.这条直线叫做二面角的棱,这两个半平面叫做
二面角的面.记作二面角α-AB-β(简记为 P-AB-Q).
2.二面角的平面角:在二面角α-l-β的棱 l 上任取一点
O,以点 O 为垂足,在半平面α,β内分别作垂直于棱 l 的射线
OA和 OB,则射线 OA 和 OB 构成的∠AOB 叫做二面角的平面角.
二面角的范围:0°≤θ≤180°. 3.面面垂直的定义:两个平面相交,如果它们所成的二面
角是直二面角,就说这两个平面互相垂直.记作α⊥β.
4.面面垂直的判定定理:一个平面过另一个平面的垂线,
则这两个平面垂直(线面垂直→面面垂直).难点求二面角的平面角 要求二面角的平面角,关键是根据图形自身特点找出二面
角的平面角,主要方法有:定义法,垂面法,三垂线定理法.
步骤为作,证,求.面面垂直的判定例 1:如图 2,P 是△ABC 所在平面外一点,AP、AB、AC两两垂直.求证:平面 PAC⊥平面 PAB.图 21-1.已知直线 m、n 和平面α、β,下列四个命题中,正确的是()DA.若 m∥α,n∥α,则 m∥n
B.若 m?α,n?α,m∥β,n∥β,则α∥β
C.若α⊥β,m?α,则 m⊥β
D.若α⊥β,m⊥β,m?α,则 m∥α用定义求二面角的平面角的大小面 ABD 与平面 BCD 所成的二面角的大小.图 32-1.下列说法正确的是()DA.二面角的大小范围是大于 0°且小于 90°
B.一个二面角的平面角可以不相等
C.二面角的平面角的顶点可以不在棱上
D.二面角的棱和二面角的平面角所在的平面垂直
A()A.60°B.90°C.45°D.120°
2-2.在正三角形 ABC 中,AD⊥BC 于 D,沿 AD 折成二面 图 4在证明线面平行时,利用中位线的性质证明线线平行,从而得出线面平行,是立体几何中常用的证明方法.3-1.如图 5,已知四边形 ABCD 为矩形,PA ⊥平面 ABCD,M、N、E 分别是 AB、PC、CD 的中点.(1)求证:MN∥平面 PAD;(2)当 MN⊥平面 PCD 时,求二面角 P—CD—B 的大小.图 5 ∴AQ⊥平面 PDC,∴AQ⊥PD.
∵Q 为 PD 的中点,
∴△PAD 为等腰直角三角形,
∴∠PDA=45°,即二面角 P-CD-B 的大小为 45°.错因剖析:考虑不全面,作图可知有两种情况.
正解:D4-1.下列命题中,假命题的个数为()B ①与三角形两边平行的平面平行于这个三角形的第三边;
②与三角形两边垂直的直线垂直于第三边;③与三角形三顶点
等距离的平面平行于这个三角形所在平面.A.0B.1C.2D.3 解析:③是假命题,如果三个顶点不在平面的同侧,则该
平面与三角形所在的平面相交.
