高一数学 4.1.1 圆的标准方程公开课课件 新人教A版必修2
文档属性
| 名称 | 高一数学 4.1.1 圆的标准方程公开课课件 新人教A版必修2 |  | |
| 格式 | zip | ||
| 文件大小 | 500.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 15:11:36 | ||
图片预览





文档简介
课件19张PPT。4.1.1 圆的标准方程生活中的圆复习引入探究新知应用举例课堂小结课后作业复习引入问题一:什么是圆?初中时我们是怎样给圆下定义的? 平面内与定点距离等于定长的点的集合(
轨迹)是圆。问题二:平面直角坐标系中,如何确定一个
圆?圆心:确定圆的位置
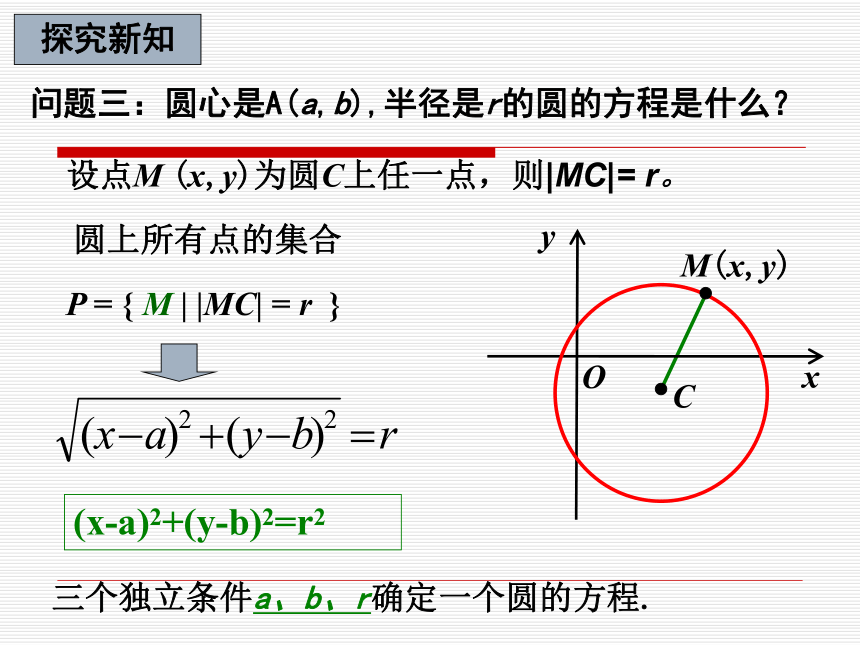
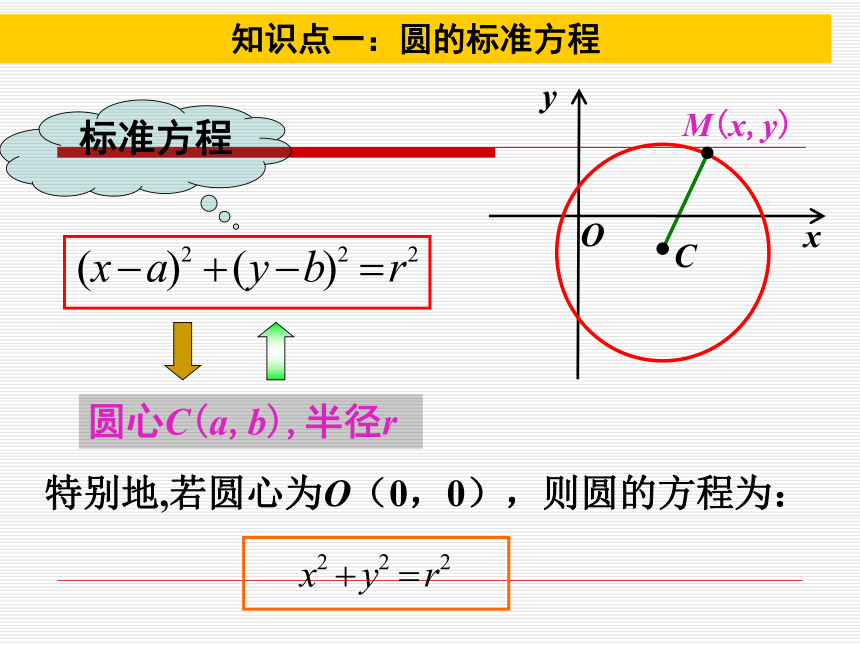
半径:确定圆的大小问题三:圆心是A(a,b),半径是r的圆的方程是什么?xyOCM(x,y)P = { M | |MC| = r }圆上所有点的集合(x-a)2+(y-b)2=r2三个独立条件a、b、r确定一个圆的方程.设点M (x,y)为圆C上任一点,则|MC|= r。 问题:是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上? 点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.想一想?xyOCM(x,y)圆心C(a,b),半径r特别地,若圆心为O(0,0),则圆的方程为:标准方程
知识点一:圆的标准方程 1.说出下列圆的方程:
(1) 圆心在原点,半径为3.
(2) 圆心在点C(3, -4), 半径为7.
(3)经过点P(5,1),圆心在点C(8,-3).2. 说出下列方程所表示的圆的圆心坐标和半径:(1) (x + 7)2 + ( y ? 4)2 = 36 (2) x2 + y2 ? 4x + 10y + 28 = 0 (3) (x ? a)2 + y 2 = m2 特殊位置的圆的方程: 圆心在原点: x2 + y2 = r2 (r≠0)圆心在x轴上: (x ? a)2 + y2 = r2 (r≠0) 圆心在y轴上: x2+ (y ? b)2 = r2 (r≠0) 圆过原点: (x ? a)2 + (y-b)2 = b2 (b≠0)圆心在x轴上且过原点: (x ? a)2 + y2 = a2 (a≠0)圆心在y轴上且过原点: x 2 + (y-b)2 = b2 (b≠0)圆与x轴相切: (x ? a)2 + (y-b)2 = a2+b2 (a2+b2≠0)圆与y轴相切: (x ? a)2 + (y-b)2 = a2 (a≠0)圆与x,y轴都相切: (x ? a)2 + (y±a)2 = a2 (a≠0) 例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上。 解:圆心是 ,半径长等于5的圆的标准方程是: 把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点
在这个圆上;典型例题 把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上.知识探究二:点与圆的位置关系 探究:在平面几何中,如何确定点与圆的位置关 系?MO|OM|r点在圆内点在圆上点在圆外(x0-a)2+(y0-b)2>r2时,点M在圆C外;(x0-a)2+(y0-b)2=r2时,点M在圆C上;(x0-a)2+(y0-b)2待定系数法解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,8)都在圆上所求圆的方程为例2 ⊿ABC的三个顶点的坐标分别是A(5,1),
B(7,-3),C(2,-8),求它的外接圆的方程。解:∵A(1,1),B(2,-2)例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.即:x-3y-3=0∴圆心C(-3,-2)例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.圆经过A(1,1),B(2,-2)解2:设圆C的方程为∵圆心在直线l:x-y+1=0上待定系数法练习2.根据下列条件,求圆的方程:
(1)求过两点A(0,4)和B(4,6),且圆心在直线x-y+1=0上的圆的标准方程。
(2)圆心在直线5x-3y=8上,又与两坐标轴相切,求圆的方程。
(3)求以C(1,3)为圆心,且和直线3x-4y-7=0相切的直线的方程。1.点(2a, 1 ? a)在圆x2 + y2 = 4的内部,求实数 a 的取值范围.例 已知圆的方程是x2 + y2 = r2,求经过圆上一 点 的切线的方程。
解:1.圆的标准方程(圆心C(a,b),半径r)2.点与圆的位置关系3.求圆的标准方程的方法:
①待定系数法
②几何性质法小结作业:课时作业(二十四)谢谢!
轨迹)是圆。问题二:平面直角坐标系中,如何确定一个
圆?圆心:确定圆的位置
半径:确定圆的大小问题三:圆心是A(a,b),半径是r的圆的方程是什么?xyOCM(x,y)P = { M | |MC| = r }圆上所有点的集合(x-a)2+(y-b)2=r2三个独立条件a、b、r确定一个圆的方程.设点M (x,y)为圆C上任一点,则|MC|= r。 问题:是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上? 点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.想一想?xyOCM(x,y)圆心C(a,b),半径r特别地,若圆心为O(0,0),则圆的方程为:标准方程
知识点一:圆的标准方程 1.说出下列圆的方程:
(1) 圆心在原点,半径为3.
(2) 圆心在点C(3, -4), 半径为7.
(3)经过点P(5,1),圆心在点C(8,-3).2. 说出下列方程所表示的圆的圆心坐标和半径:(1) (x + 7)2 + ( y ? 4)2 = 36 (2) x2 + y2 ? 4x + 10y + 28 = 0 (3) (x ? a)2 + y 2 = m2 特殊位置的圆的方程: 圆心在原点: x2 + y2 = r2 (r≠0)圆心在x轴上: (x ? a)2 + y2 = r2 (r≠0) 圆心在y轴上: x2+ (y ? b)2 = r2 (r≠0) 圆过原点: (x ? a)2 + (y-b)2 = b2 (b≠0)圆心在x轴上且过原点: (x ? a)2 + y2 = a2 (a≠0)圆心在y轴上且过原点: x 2 + (y-b)2 = b2 (b≠0)圆与x轴相切: (x ? a)2 + (y-b)2 = a2+b2 (a2+b2≠0)圆与y轴相切: (x ? a)2 + (y-b)2 = a2 (a≠0)圆与x,y轴都相切: (x ? a)2 + (y±a)2 = a2 (a≠0) 例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上。 解:圆心是 ,半径长等于5的圆的标准方程是: 把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点
在这个圆上;典型例题 把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上.知识探究二:点与圆的位置关系 探究:在平面几何中,如何确定点与圆的位置关 系?MO|OM|
B(7,-3),C(2,-8),求它的外接圆的方程。解:∵A(1,1),B(2,-2)例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.即:x-3y-3=0∴圆心C(-3,-2)例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.圆经过A(1,1),B(2,-2)解2:设圆C的方程为∵圆心在直线l:x-y+1=0上待定系数法练习2.根据下列条件,求圆的方程:
(1)求过两点A(0,4)和B(4,6),且圆心在直线x-y+1=0上的圆的标准方程。
(2)圆心在直线5x-3y=8上,又与两坐标轴相切,求圆的方程。
(3)求以C(1,3)为圆心,且和直线3x-4y-7=0相切的直线的方程。1.点(2a, 1 ? a)在圆x2 + y2 = 4的内部,求实数 a 的取值范围.例 已知圆的方程是x2 + y2 = r2,求经过圆上一 点 的切线的方程。
解:1.圆的标准方程(圆心C(a,b),半径r)2.点与圆的位置关系3.求圆的标准方程的方法:
①待定系数法
②几何性质法小结作业:课时作业(二十四)谢谢!
