高一数学 4.2.2 圆与圆的位置关系课件 新人教A版必修2
文档属性
| 名称 | 高一数学 4.2.2 圆与圆的位置关系课件 新人教A版必修2 |  | |
| 格式 | zip | ||
| 文件大小 | 244.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 15:12:28 | ||
图片预览






文档简介
课件17张PPT。 4.2.2 圆与圆的位置关系
1.经过圆 C:(x+1)2+(y-2)2=4 的圆心且斜率为 1 的直线方程为()AA.x-y+3=0
C.x+y-1=0B.x-y-3=0
D.x+y+3=02.设 r>0,圆 (x-1)2+(y+3)2=r2与 x2+y2=16 的位置关系不可能是()DA.相切
C.内含和内切B.相交
D.外切和外离3.两圆 x2+y2-4x+6y=0 和 x2+y2-6x=0 的连心线方程为()CA.x+y+3=0
C.3x-y-9=0B.2x-y-5=0
D.4x-3y+7=0 4.圆 x2+y2+2x+6y-19=0 与圆 x2+y2-6x+2y-10=0
的两圆心之间的距离是_____.
5.经过两圆 x2+y2-2x+2y-7=0 和 x2+y2+4x-4y-8
=0 的两个交点的直线的方程是_____________. 6x-6y-1=0 解析:两圆的方程相减得-6x+6y+1=0,即 6x-6y-1=
0.此方程表示的曲线过两个圆的交点.重点圆与圆的位置关系及判定方法圆 C1:(x-a1)2+(y-b1)2=R2,
圆 C2:(x-a2)2+(y-b2)2=r2(R>r).
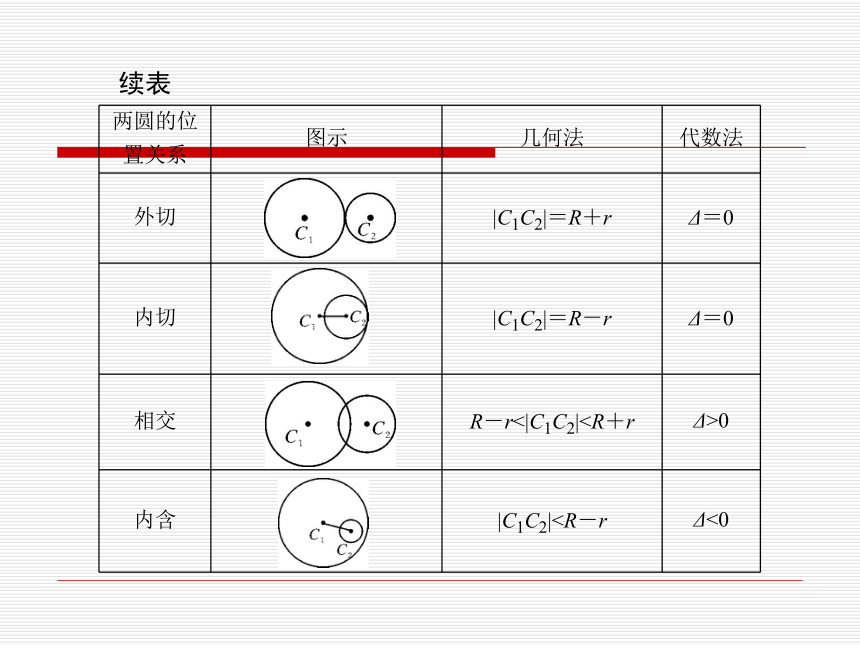
两圆的位置关系如下表:续表难点两圆的公切线 和两个圆都相切的直线称为两圆的公切线,公切线条数如
下表:判断圆与圆的位置关系例 1:判断圆 C1:x2+y2-2mx+4y+m2-5=0 与圆 C2:x2+y2+2x-2my+m2-3=0 的位置关系. 1-1.已知圆 C1:x2+y2-6x-6=0,圆 C2:x2+y2-4y-6
=0,试判断两圆的位置关系. 求相交圆的公共弦长
例 2:求圆 x2+y2-4=0 与圆 x2+y2-4x+4y-12=0 的公
共弦的长. 思维突破:可用方程思想和几何法两种方法,几何法更为
简便:先求出公共弦所在直线方程,再通过直角三角形求解. 涉及圆的弦长问题,通常考虑由半径 r、圆
心到直线的距离 d、弦长的一半构成的直角三角形求解,即公共
2-1.已知圆 C1:x2+y2-10x-10y=0 和圆 C2:x2+y2+6x
+2y-40=0 相交于 A、B 两点,求公共弦 AB 的长. 圆系方程的应用
例 3:求经过两圆 x2+y2+6x-4=0 和 x2+y2+6y-28=0
的交点,并且圆心在直线 x-y-4=0 上的圆的方程. 思维突破:经过两圆交点的圆的方程可用圆系方程形式设
出,其中待定系数可依据圆心在已知直线上求得. 3-1.已知圆 x2+y2+x-6y+3=0 与直线 x+2y-3=0 的两
个交点为 P、Q,求以 PQ 为直径的圆的方程. 例 4:集合 A={(x,y)|x2+y2=4}和 B={(x,y)|(x-3)2+(y
-4)2=r2},其中 r>0,若 A∩B 中有且仅有一个元素,则 r 的
值是________.错因剖析:两圆相切包括内切或外切,这里很容易漏解.正解:3 或 7-1x2+(y-1)2=1
1.经过圆 C:(x+1)2+(y-2)2=4 的圆心且斜率为 1 的直线方程为()AA.x-y+3=0
C.x+y-1=0B.x-y-3=0
D.x+y+3=02.设 r>0,圆 (x-1)2+(y+3)2=r2与 x2+y2=16 的位置关系不可能是()DA.相切
C.内含和内切B.相交
D.外切和外离3.两圆 x2+y2-4x+6y=0 和 x2+y2-6x=0 的连心线方程为()CA.x+y+3=0
C.3x-y-9=0B.2x-y-5=0
D.4x-3y+7=0 4.圆 x2+y2+2x+6y-19=0 与圆 x2+y2-6x+2y-10=0
的两圆心之间的距离是_____.
5.经过两圆 x2+y2-2x+2y-7=0 和 x2+y2+4x-4y-8
=0 的两个交点的直线的方程是_____________. 6x-6y-1=0 解析:两圆的方程相减得-6x+6y+1=0,即 6x-6y-1=
0.此方程表示的曲线过两个圆的交点.重点圆与圆的位置关系及判定方法圆 C1:(x-a1)2+(y-b1)2=R2,
圆 C2:(x-a2)2+(y-b2)2=r2(R>r).
两圆的位置关系如下表:续表难点两圆的公切线 和两个圆都相切的直线称为两圆的公切线,公切线条数如
下表:判断圆与圆的位置关系例 1:判断圆 C1:x2+y2-2mx+4y+m2-5=0 与圆 C2:x2+y2+2x-2my+m2-3=0 的位置关系. 1-1.已知圆 C1:x2+y2-6x-6=0,圆 C2:x2+y2-4y-6
=0,试判断两圆的位置关系. 求相交圆的公共弦长
例 2:求圆 x2+y2-4=0 与圆 x2+y2-4x+4y-12=0 的公
共弦的长. 思维突破:可用方程思想和几何法两种方法,几何法更为
简便:先求出公共弦所在直线方程,再通过直角三角形求解. 涉及圆的弦长问题,通常考虑由半径 r、圆
心到直线的距离 d、弦长的一半构成的直角三角形求解,即公共
2-1.已知圆 C1:x2+y2-10x-10y=0 和圆 C2:x2+y2+6x
+2y-40=0 相交于 A、B 两点,求公共弦 AB 的长. 圆系方程的应用
例 3:求经过两圆 x2+y2+6x-4=0 和 x2+y2+6y-28=0
的交点,并且圆心在直线 x-y-4=0 上的圆的方程. 思维突破:经过两圆交点的圆的方程可用圆系方程形式设
出,其中待定系数可依据圆心在已知直线上求得. 3-1.已知圆 x2+y2+x-6y+3=0 与直线 x+2y-3=0 的两
个交点为 P、Q,求以 PQ 为直径的圆的方程. 例 4:集合 A={(x,y)|x2+y2=4}和 B={(x,y)|(x-3)2+(y
-4)2=r2},其中 r>0,若 A∩B 中有且仅有一个元素,则 r 的
值是________.错因剖析:两圆相切包括内切或外切,这里很容易漏解.正解:3 或 7-1x2+(y-1)2=1
