人教A版(2019)高中数学选择性必修第一册 课时作业:3.2.2双曲线的简单几何性质(含解析)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 课时作业:3.2.2双曲线的简单几何性质(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 11:57:10 | ||
图片预览
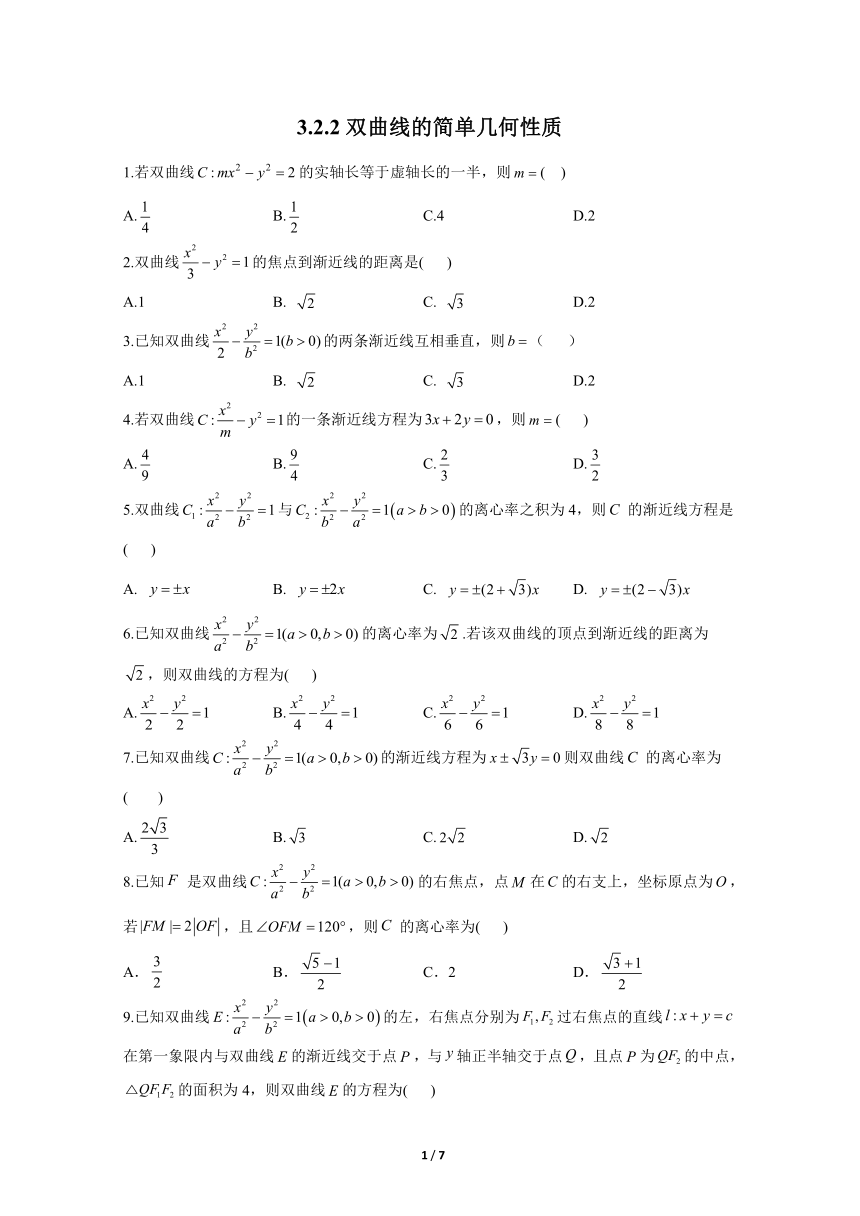


文档简介
3.2.2双曲线的简单几何性质
1.若双曲线的实轴长等于虚轴长的一半,则( )
A. B. C.4 D.2
2.双曲线的焦点到渐近线的距离是( )
A.1 B. C. D.2
3.已知双曲线的两条渐近线互相垂直,则( )
A.1 B. C. D.2
4.若双曲线的一条渐近线方程为,则( )
A. B. C. D.
5.双曲线与的离心率之积为4,则的渐近线方程是( )
A. B. C. D.
6.已知双曲线的离心率为.若该双曲线的顶点到渐近线的距离为,则双曲线的方程为( )
A. B. C. D.
7.已知双曲线的渐近线方程为则双曲线的离心率为( )
A. B. C. D.
8.已知是双曲线的右焦点,点在的右支上,坐标原点为,若,且,则的离心率为( )
A. B. C.2 D.
9.已知双曲线的左,右焦点分别为过右焦点的直线在第一象限内与双曲线的渐近线交于点,与轴正半轴交于点,且点为的中点,的面积为4,则双曲线的方程为( )
A. B.
C. D.
10.在平面直角坐标系中,若双曲线的一条渐近线方程为,则该双曲线的离心率是____________.
11.已知双曲线的一条渐近线方程为,若其右顶点到这条渐近线的距离为,则双曲线方程为____________.
12.已知左、右焦点分别为的双曲线的一条渐近线与直线相互垂直,点在双曲线上,且,则双曲线的焦距为___________.
13.分别是双曲线的左,右焦点,过且斜率为1的直线分别与双曲线的两条渐近线交于,若B为的中点,则该曲线的渐近线方程是_______.
14.已知双曲线的右焦点为.
(1)若双曲线的一条渐近线方程为且,求双曲线的方程;
(2)以原点O为圆心,c为半径作圆,该圆与双曲线在第一象限的交点为A,过点A作圆的切线,斜率为,求双曲线的离心率.
答案以及解析
1.答案:C
解析:双曲线化为标准方程是,由于实轴长是虚轴长的一半,故,解得.故选C.
2.答案:A
解析:在双曲线方程中, 不妨设双曲线的右焦点为,则又双曲线的一条渐近线方程为,即∴焦点到渐近线的距离
3.答案:B
解析:双曲线是焦点在轴上的双曲线,
,则渐近线方程为,
∵两条渐近线互相垂直,∴,即.
4.答案:A
解析:由题意知,双曲线的渐近线方程为可化为,所以解得.
5.答案:D
解析:由已知,即,∴,∴. 变形得,∵,故,
∴双曲线的渐近线方程为.
6.答案:B
解析:设双曲线的右顶点为.根据双曲线与渐近线的对称性,不妨设渐近线为,则点到渐近线的距离为,即.而.故选B.
7.答案:A
解析:由题知,又,解得.
8.答案:D
解析:由题意可得,
即有,
即有,
由双曲线的定义可得,即为,
即有,可得.
故选D.
9.答案:A
解析:双曲线的一条渐近线方程为,代入直线,可得,且,点为的中点,可得,可得,的面积为4,即,解得,则双曲线的方程为.故选A.
10.答案:
解析:由双曲线的一条渐近线方程为得,
则该双曲线的离心率.
11.答案:
解析:根据题意,双曲线渐近线方程为,
顶点坐标,顶点到渐近线的距离为:,解得,
根据渐近线方程的斜率,可得,
所以双曲线的方程为:;
故答案为:.
12.答案:
解析:依题意,直线的斜率为,故,则,因为,故,故,故.
13.答案:
解析:设直线方程为(c为双曲线的半焦距),依题意知,点A是直线与渐近线的交点,易得;点B是直线与渐近线的交点,易得,因为B为的中点,所以,即,即,即,所以该双曲线的渐近线方程为
14.答案:(1)∵双曲线的渐近线方程为,∴,
∴,得.
∴双曲线方程为.
(2)设点A的坐标为,
则直线的斜率满足,
∴,①
依题意,圆的方程为,
将①代入圆的方程得,即,
∴,∴点A的坐标为,
代入双曲线方程得,
即.②
又∵,
∴将代入②式,整理得
,
∴,得,
∵,∴,即双曲线的离心率为.
PAGE
1 / 3
1.若双曲线的实轴长等于虚轴长的一半,则( )
A. B. C.4 D.2
2.双曲线的焦点到渐近线的距离是( )
A.1 B. C. D.2
3.已知双曲线的两条渐近线互相垂直,则( )
A.1 B. C. D.2
4.若双曲线的一条渐近线方程为,则( )
A. B. C. D.
5.双曲线与的离心率之积为4,则的渐近线方程是( )
A. B. C. D.
6.已知双曲线的离心率为.若该双曲线的顶点到渐近线的距离为,则双曲线的方程为( )
A. B. C. D.
7.已知双曲线的渐近线方程为则双曲线的离心率为( )
A. B. C. D.
8.已知是双曲线的右焦点,点在的右支上,坐标原点为,若,且,则的离心率为( )
A. B. C.2 D.
9.已知双曲线的左,右焦点分别为过右焦点的直线在第一象限内与双曲线的渐近线交于点,与轴正半轴交于点,且点为的中点,的面积为4,则双曲线的方程为( )
A. B.
C. D.
10.在平面直角坐标系中,若双曲线的一条渐近线方程为,则该双曲线的离心率是____________.
11.已知双曲线的一条渐近线方程为,若其右顶点到这条渐近线的距离为,则双曲线方程为____________.
12.已知左、右焦点分别为的双曲线的一条渐近线与直线相互垂直,点在双曲线上,且,则双曲线的焦距为___________.
13.分别是双曲线的左,右焦点,过且斜率为1的直线分别与双曲线的两条渐近线交于,若B为的中点,则该曲线的渐近线方程是_______.
14.已知双曲线的右焦点为.
(1)若双曲线的一条渐近线方程为且,求双曲线的方程;
(2)以原点O为圆心,c为半径作圆,该圆与双曲线在第一象限的交点为A,过点A作圆的切线,斜率为,求双曲线的离心率.
答案以及解析
1.答案:C
解析:双曲线化为标准方程是,由于实轴长是虚轴长的一半,故,解得.故选C.
2.答案:A
解析:在双曲线方程中, 不妨设双曲线的右焦点为,则又双曲线的一条渐近线方程为,即∴焦点到渐近线的距离
3.答案:B
解析:双曲线是焦点在轴上的双曲线,
,则渐近线方程为,
∵两条渐近线互相垂直,∴,即.
4.答案:A
解析:由题意知,双曲线的渐近线方程为可化为,所以解得.
5.答案:D
解析:由已知,即,∴,∴. 变形得,∵,故,
∴双曲线的渐近线方程为.
6.答案:B
解析:设双曲线的右顶点为.根据双曲线与渐近线的对称性,不妨设渐近线为,则点到渐近线的距离为,即.而.故选B.
7.答案:A
解析:由题知,又,解得.
8.答案:D
解析:由题意可得,
即有,
即有,
由双曲线的定义可得,即为,
即有,可得.
故选D.
9.答案:A
解析:双曲线的一条渐近线方程为,代入直线,可得,且,点为的中点,可得,可得,的面积为4,即,解得,则双曲线的方程为.故选A.
10.答案:
解析:由双曲线的一条渐近线方程为得,
则该双曲线的离心率.
11.答案:
解析:根据题意,双曲线渐近线方程为,
顶点坐标,顶点到渐近线的距离为:,解得,
根据渐近线方程的斜率,可得,
所以双曲线的方程为:;
故答案为:.
12.答案:
解析:依题意,直线的斜率为,故,则,因为,故,故,故.
13.答案:
解析:设直线方程为(c为双曲线的半焦距),依题意知,点A是直线与渐近线的交点,易得;点B是直线与渐近线的交点,易得,因为B为的中点,所以,即,即,即,所以该双曲线的渐近线方程为
14.答案:(1)∵双曲线的渐近线方程为,∴,
∴,得.
∴双曲线方程为.
(2)设点A的坐标为,
则直线的斜率满足,
∴,①
依题意,圆的方程为,
将①代入圆的方程得,即,
∴,∴点A的坐标为,
代入双曲线方程得,
即.②
又∵,
∴将代入②式,整理得
,
∴,得,
∵,∴,即双曲线的离心率为.
PAGE
1 / 3
