14.1直角三角形的三边关系-勾股定理
文档属性
| 名称 | 14.1直角三角形的三边关系-勾股定理 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-14 11:18:38 | ||
图片预览







文档简介
课件30张PPT。14.1勾股定理黔江区舟白中学--粟永镇
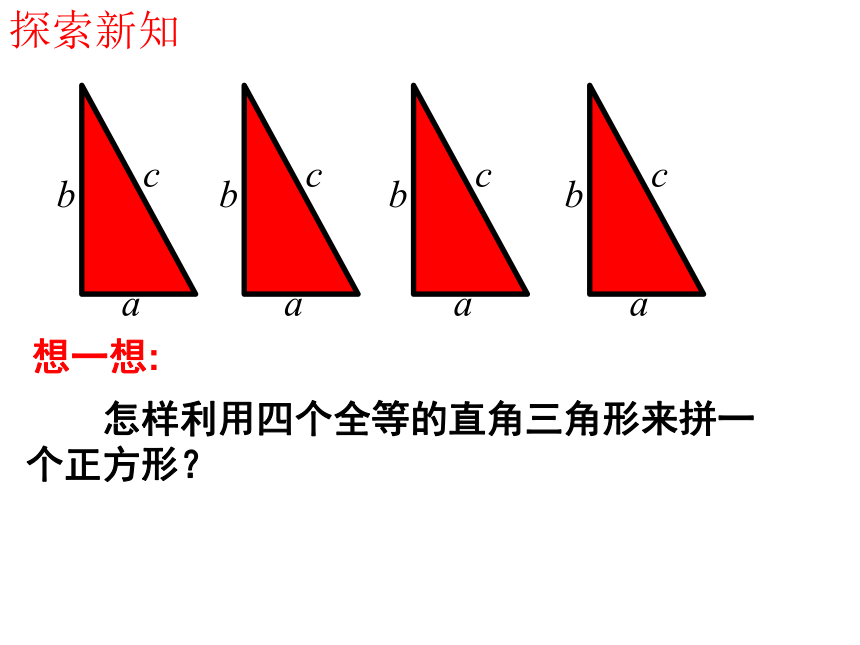
E-Mail:416352289@qq.com 怎样利用四个全等的直角三角形来拼一
个正方形?想一想:探索新知方法一:你能用两种方法表示大正方形的面积吗?大正方形的面积
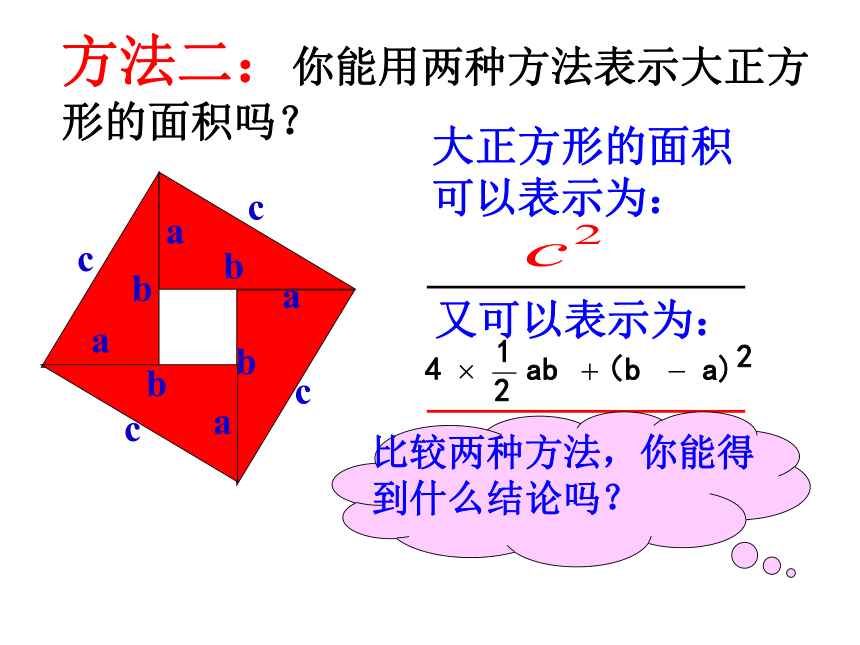
可以表示为:又可以表示为:比较得:即方法二:你能用两种方法表示大正方形的面积吗?大正方形的面积
可以表示为:又可以表示为:比较得:即 如果直角三角形的两条直角边为a、b,斜边为c,那么
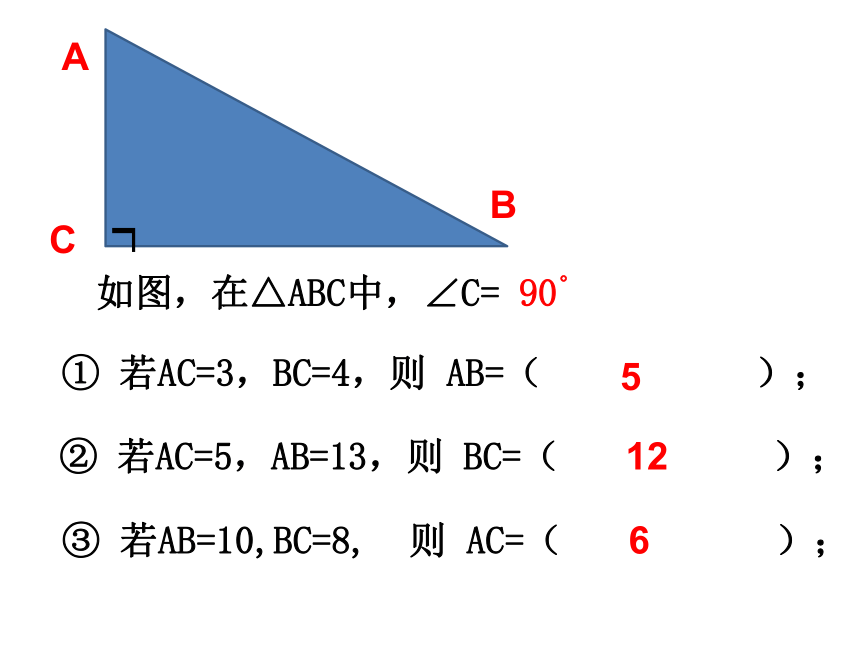
________________ a2+b2=c2勾股定理 直角三角形两直角边的平方和即 等于斜边的平方.① 若AC=3,BC=4,则 AB=( );② 若AC=5,AB=13,则 BC=( );③ 若AB=10,BC=8, 则 AC=( );如图,在△ABC中,∠C= 90。5126 中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
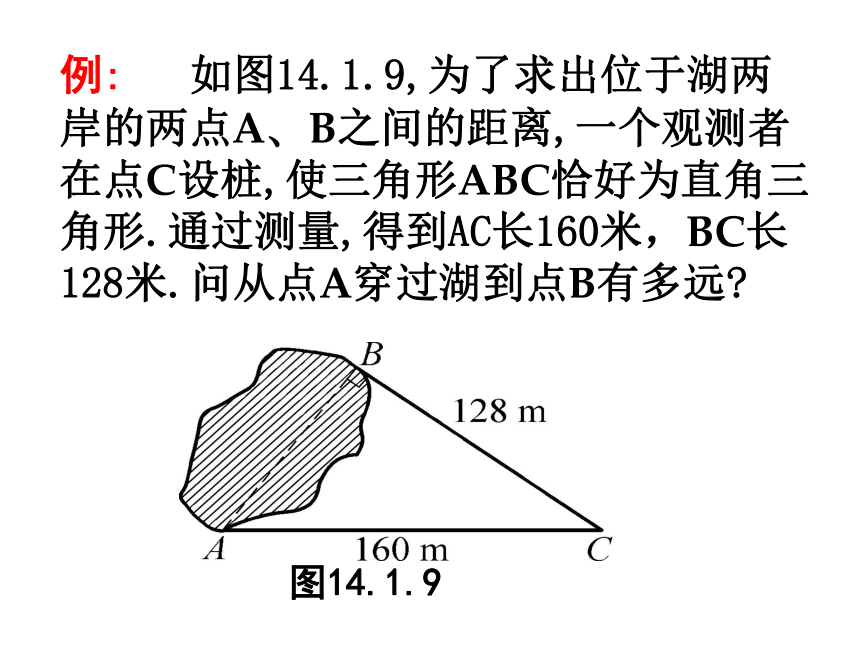
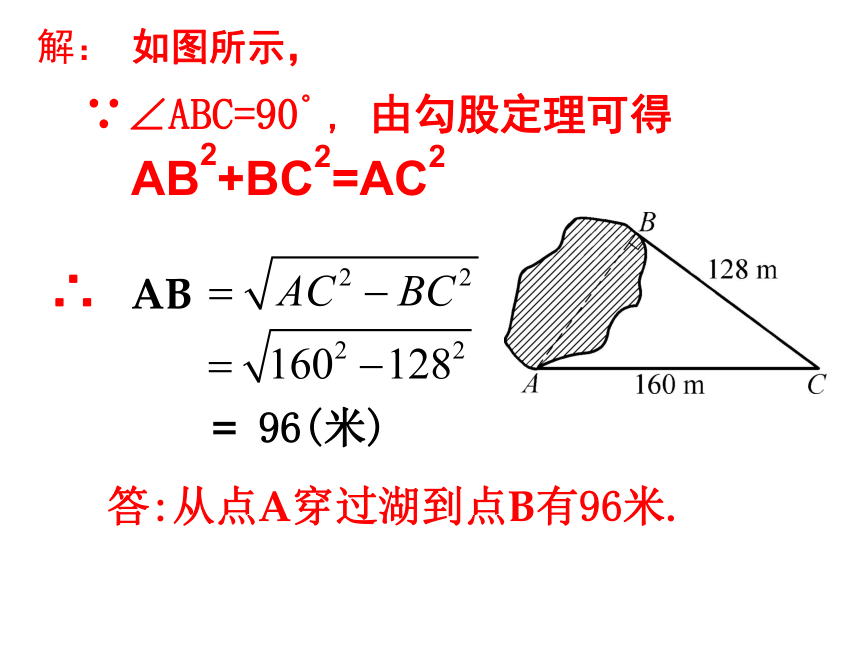
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。毕达哥拉斯 在国外,相传勾股定理是公元前550年古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。 例: 如图14.1.9,为了求出位于湖两岸的两点A、B之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
解: 如图所示,= 96(米)AB答:从点A穿过湖到点B有96米.AB2+BC2=AC2∴∵∠ABC=90。, 由勾股定理可得 假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们在A点登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?AB82361C解:如图所示,在△ABC中,∠ACB=90。,
AC=6km,BC=8km,由勾股定理得AC2+BC2=AB2∴AB ==10km答:登陆点A 到宝藏埋藏点B的距离是10千米.课堂小练习1.如图,在Rt△ABC中, ∠C = 90°,7813abc2.判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2. ( ) ×× 2) 直角三角形的两边长分别是3和4,则第三边长是5. ( ) 第三边的长是多少呢? 蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE做
一
做AB=5cmBC=13cmCD=10cm蚂蚁从A到D一共爬了28cm 如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长. EFGH1.已知一个直角三角形斜边长17厘米、一条直角边长15厘米,求这个三角形的面积.解: 如 图, 设另一条直角边长是 x 厘米.由勾股定理得: 即 x2 = 172 - 152= 289 – 225 = 64∴ x=8∴直角三角形的面积是:
(平方厘米)课堂练习152 + x2 = 1722.在一场强大的台风中,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高? 小丁的妈妈买了一部34英寸(86厘米)的电视机。小丁量了电视机的屏幕后,发现屏幕只有70厘米长和50厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错荧屏对角线大约为86厘米∵702+502=7400862=7396应用扩展1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想 如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49? 议一议 美丽的勾股树(一)欣赏美丽的勾股树(二)欣赏如图,在Rt△ABC中,∠BAC=90。,AD是BC上的高,AB=5,AC=12.求高AD的长ABCD解:如图所示∵∠BAC=90。
AB=5,AC=12∴BC==13∴解得 AD=又∵ 如图,工人师傅要将这几级梯步铺上地毯,梯步的水平跨度BC=4米,倾斜面的长度AC=5米,每级梯步长AD=5米,请你帮忙算一算工人师傅需要多少平米的地毯?解:如图所示∵∠B=90。由勾股定理得=3∵ 梯步的展开是一个矩形,其中一边长为AD=5米,
另一边长为AB+BC=7米∴ 面积=AD(AB+BC)
=5 x 7
=35m2答:工人师傅需要35平方米的地毯ABCDEF如图,在长方形ABCD 中,长AD=10cm,宽AB=8cm,
将长方形沿着折痕AE翻折,使点D刚好落在边BC上
的点F处。求CF的长解:如图所示∵ AD=AF=10cm
AB=8cm ∠B =90。∴ BF==6cm又∵BC=AD=10cm∴CF=BC-BF
=10-6
=4cm怎么求CE的长呢?ABCDEF ∵ EF=DE又∵ ∠C =90。∴ 即 解得 CE=3即 CE=3cm能否求折痕AE的长呢?∴EF=DE=8-CE△AEF的面积呢?如图,在△ABC中,∠C=90。,
AC=6,AB=10,AD平分∠BAC,
DE⊥AB于E,求CD的长.解:如图所示∵ AD平分∠BAC,DC⊥AC, DE⊥AB∴ CD=DE在Rt△ACD与Rt△AED中,∵ AD=AD DC=DE∴Rt△ACD≌Rt△AED(H L )∴AE=AC=6∴BE=AB-AE=10-6=4又∵BC==8且 BC=BD+CD=BD+DE∴BD=8-DE在Rt△BED中,由勾股定理得解得 DE=3∴ CD=3怎么求AD呢? 1.利用拼图来验证勾股定理:同一图形的面积等式化简结论 2.构造直角三角形,应用勾股定理解决简单的实际问题用两种方法表示正方形作业布置
(略)
个正方形?想一想:探索新知方法一:你能用两种方法表示大正方形的面积吗?大正方形的面积
可以表示为:又可以表示为:比较得:即方法二:你能用两种方法表示大正方形的面积吗?大正方形的面积
可以表示为:又可以表示为:比较得:即 如果直角三角形的两条直角边为a、b,斜边为c,那么
________________ a2+b2=c2勾股定理 直角三角形两直角边的平方和即 等于斜边的平方.① 若AC=3,BC=4,则 AB=( );② 若AC=5,AB=13,则 BC=( );③ 若AB=10,BC=8, 则 AC=( );如图,在△ABC中,∠C= 90。5126 中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。毕达哥拉斯 在国外,相传勾股定理是公元前550年古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。 例: 如图14.1.9,为了求出位于湖两岸的两点A、B之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
解: 如图所示,= 96(米)AB答:从点A穿过湖到点B有96米.AB2+BC2=AC2∴∵∠ABC=90。, 由勾股定理可得 假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们在A点登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?AB82361C解:如图所示,在△ABC中,∠ACB=90。,
AC=6km,BC=8km,由勾股定理得AC2+BC2=AB2∴AB ==10km答:登陆点A 到宝藏埋藏点B的距离是10千米.课堂小练习1.如图,在Rt△ABC中, ∠C = 90°,7813abc2.判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2. ( ) ×× 2) 直角三角形的两边长分别是3和4,则第三边长是5. ( ) 第三边的长是多少呢? 蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE做
一
做AB=5cmBC=13cmCD=10cm蚂蚁从A到D一共爬了28cm 如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长. EFGH1.已知一个直角三角形斜边长17厘米、一条直角边长15厘米,求这个三角形的面积.解: 如 图, 设另一条直角边长是 x 厘米.由勾股定理得: 即 x2 = 172 - 152= 289 – 225 = 64∴ x=8∴直角三角形的面积是:
(平方厘米)课堂练习152 + x2 = 1722.在一场强大的台风中,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高? 小丁的妈妈买了一部34英寸(86厘米)的电视机。小丁量了电视机的屏幕后,发现屏幕只有70厘米长和50厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错荧屏对角线大约为86厘米∵702+502=7400862=7396应用扩展1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想 如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49? 议一议 美丽的勾股树(一)欣赏美丽的勾股树(二)欣赏如图,在Rt△ABC中,∠BAC=90。,AD是BC上的高,AB=5,AC=12.求高AD的长ABCD解:如图所示∵∠BAC=90。
AB=5,AC=12∴BC==13∴解得 AD=又∵ 如图,工人师傅要将这几级梯步铺上地毯,梯步的水平跨度BC=4米,倾斜面的长度AC=5米,每级梯步长AD=5米,请你帮忙算一算工人师傅需要多少平米的地毯?解:如图所示∵∠B=90。由勾股定理得=3∵ 梯步的展开是一个矩形,其中一边长为AD=5米,
另一边长为AB+BC=7米∴ 面积=AD(AB+BC)
=5 x 7
=35m2答:工人师傅需要35平方米的地毯ABCDEF如图,在长方形ABCD 中,长AD=10cm,宽AB=8cm,
将长方形沿着折痕AE翻折,使点D刚好落在边BC上
的点F处。求CF的长解:如图所示∵ AD=AF=10cm
AB=8cm ∠B =90。∴ BF==6cm又∵BC=AD=10cm∴CF=BC-BF
=10-6
=4cm怎么求CE的长呢?ABCDEF ∵ EF=DE又∵ ∠C =90。∴ 即 解得 CE=3即 CE=3cm能否求折痕AE的长呢?∴EF=DE=8-CE△AEF的面积呢?如图,在△ABC中,∠C=90。,
AC=6,AB=10,AD平分∠BAC,
DE⊥AB于E,求CD的长.解:如图所示∵ AD平分∠BAC,DC⊥AC, DE⊥AB∴ CD=DE在Rt△ACD与Rt△AED中,∵ AD=AD DC=DE∴Rt△ACD≌Rt△AED(H L )∴AE=AC=6∴BE=AB-AE=10-6=4又∵BC==8且 BC=BD+CD=BD+DE∴BD=8-DE在Rt△BED中,由勾股定理得解得 DE=3∴ CD=3怎么求AD呢? 1.利用拼图来验证勾股定理:同一图形的面积等式化简结论 2.构造直角三角形,应用勾股定理解决简单的实际问题用两种方法表示正方形作业布置
(略)
