14.1.2直角三角形的判定
图片预览






文档简介
课件18张PPT。直角三角形的判定黔江区舟白中学--粟永镇
E-Mail:416352289@qq.com那么什么样的三角形是直角三角形呢?有一个角是直角的三角形是直角三角形(定义)还有其他判断方法吗?直角三角形的性质(1)直角三角形有一个角是直角;(2)直角三角形两直角边的平方和等于斜边的平方。(勾股定理:a2+b2=c2,其中c为斜边)做 一 做 下列的三组数分别是一个三角形的三边
长a,b,c:
①3,4,5;②6,8,10;③5,12,13;(1)这三组数都满足a2+b2=c2吗?(2)分别以每组数为三边作出三角形,用
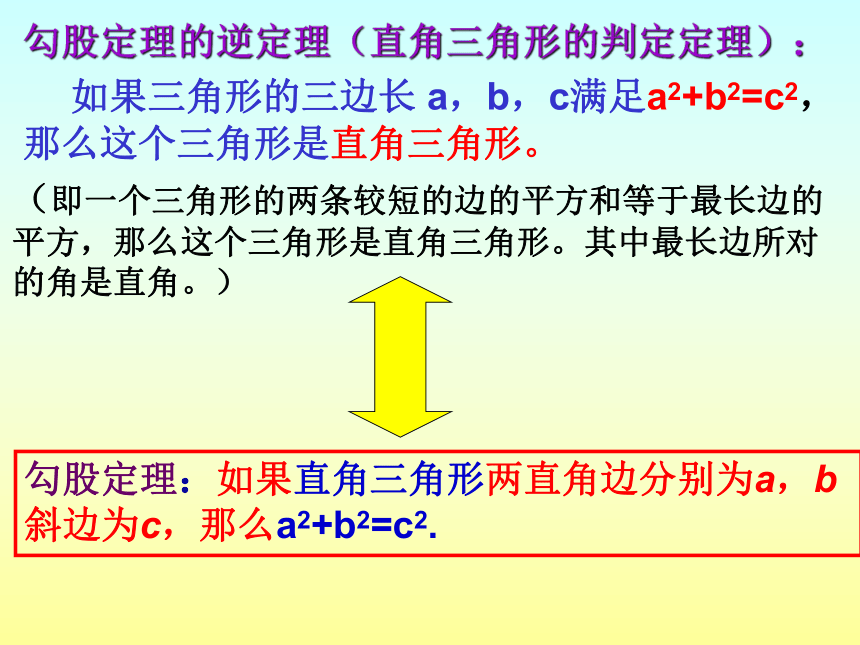
量角器量一量,它们都是直角三角形吗? 如果三角形的三边长 a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。勾股定理:如果直角三角形两直角边分别为a,b斜边为c,那么a2+b2=c2.勾股定理的逆定理(直角三角形的判定定理):(即一个三角形的两条较短的边的平方和等于最长边的平方,那么这个三角形是直角三角形。其中最长边所对的角是直角。) 如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是
直角三角形。其中满足a2+b2=c2的三个正整数, 称为勾股数。3、4、55、12、137、24、259、40、416、8、10。。。。。。8、15、17常用勾股数 设三角形的三边分别等于下列各组数,试判断各三角形是不是直角三角形?如果是请指明哪一条边所对的角是直角?(1)12,16,20 (2)8,12,15 (3)5,6,8 解:(1)是直角三角形。边20所对的角是直角(2)不是直角三角形(3)不是直角三角形练 一 练1、下列几组数是勾股数的为( )。
(A)9,12,19 (B)1.5,2,2.5
(C)7,25,24 (D)12,18,22
2、一艘帆船在海上航行,由于风向的原因,帆船先向正东方向航行9千米,然后向正北方向航行40千米,这时它离开出发点_________千米。C41例.一个零件的形状如图1所示,按规定这个零件中,∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?图1图2解:如图所示因此这个零件符合要求∴△BCD是直角三角形,∠DBC是直角∵在△BCD中,BD2+BC2=25+144=169=CD2 ∴△ABD是直角三角形,∠A是直角∵在△ABD中,AB2+AD2=9+16=25=BD2如图,四边形ABCD中,∠A=90。,已知AD=3,AB=4,CD=12,BC=13,求四边形ABCD 的面积。解:如图所示,连接BD,在Rt△ABD中,由勾股定理得∴ 四边形ABCD的面积为36在△BDC中,又∵ CD=12, BC=13, BD=5.∴△ BDC是直角三角形如图,四边形ABCD中,∠A=90。, AB=24,BC=20,CD=15,AD=7,
①求∠ABC与∠ADC的关系
②求四边形ABCD的面积; 类型演练提示:可连接BD如图,△ABC中,AB=13,BC=10,BC上的
中线AD=12. 求证:∠B=∠C证明:如图所示在△ABC中,∵ BC=10 ,AD是中线∴BD=5在△ABD中∵ AB=13、AD=12、BD=5∴ △ABD是直角三角形,∠ADB=90。∴ AD⊥BC ∴ AD是BC上的垂直平分线∴ AB=AC∴ ∠B=∠C 例. 如果a、b、c是△ABC的三边(a≠b≠c),且满足 a4-b4+b2c2-a2c2=0,试判断三角形的形状。解:由题意得∵ a4-b4+b2c2-a2c2=0即又∵ a、b、c是△ABC的三边,且a≠b≠c∴即∴ △ABC是直角三角形 例. 如果△ABC的三边 AC=m2-n2, AB=2mn,BC=m2+n2 。求证:∠A=90。证明:由题意得∵ AC=m2-n2,AB=2mn,BC=m2+n2∴= (m2-n2)2+(2mn)2即∴ △ABC是直角三角形,边BC所对的角∠A=90。 如果△ABC的三边AC=n2-1,BC=2n,AB=n2+1。试判断△ABC是直角三角形,哪条边所对的角是直角?并说明理由。类型演练补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米;D、 60/13厘米;
CD直角三角形的判定方法:1、定义(角):有一个角是90°的三角形是直角三 角形。2、勾股定理的逆定理:如果三角形的三边长a、b、c(c为最大边)满足则,这个三角形是直角三角形作业布置(略)
长a,b,c:
①3,4,5;②6,8,10;③5,12,13;(1)这三组数都满足a2+b2=c2吗?(2)分别以每组数为三边作出三角形,用
量角器量一量,它们都是直角三角形吗? 如果三角形的三边长 a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。勾股定理:如果直角三角形两直角边分别为a,b斜边为c,那么a2+b2=c2.勾股定理的逆定理(直角三角形的判定定理):(即一个三角形的两条较短的边的平方和等于最长边的平方,那么这个三角形是直角三角形。其中最长边所对的角是直角。) 如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是
直角三角形。其中满足a2+b2=c2的三个正整数, 称为勾股数。3、4、55、12、137、24、259、40、416、8、10。。。。。。8、15、17常用勾股数 设三角形的三边分别等于下列各组数,试判断各三角形是不是直角三角形?如果是请指明哪一条边所对的角是直角?(1)12,16,20 (2)8,12,15 (3)5,6,8 解:(1)是直角三角形。边20所对的角是直角(2)不是直角三角形(3)不是直角三角形练 一 练1、下列几组数是勾股数的为( )。
(A)9,12,19 (B)1.5,2,2.5
(C)7,25,24 (D)12,18,22
2、一艘帆船在海上航行,由于风向的原因,帆船先向正东方向航行9千米,然后向正北方向航行40千米,这时它离开出发点_________千米。C41例.一个零件的形状如图1所示,按规定这个零件中,∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?图1图2解:如图所示因此这个零件符合要求∴△BCD是直角三角形,∠DBC是直角∵在△BCD中,BD2+BC2=25+144=169=CD2 ∴△ABD是直角三角形,∠A是直角∵在△ABD中,AB2+AD2=9+16=25=BD2如图,四边形ABCD中,∠A=90。,已知AD=3,AB=4,CD=12,BC=13,求四边形ABCD 的面积。解:如图所示,连接BD,在Rt△ABD中,由勾股定理得∴ 四边形ABCD的面积为36在△BDC中,又∵ CD=12, BC=13, BD=5.∴△ BDC是直角三角形如图,四边形ABCD中,∠A=90。, AB=24,BC=20,CD=15,AD=7,
①求∠ABC与∠ADC的关系
②求四边形ABCD的面积; 类型演练提示:可连接BD如图,△ABC中,AB=13,BC=10,BC上的
中线AD=12. 求证:∠B=∠C证明:如图所示在△ABC中,∵ BC=10 ,AD是中线∴BD=5在△ABD中∵ AB=13、AD=12、BD=5∴ △ABD是直角三角形,∠ADB=90。∴ AD⊥BC ∴ AD是BC上的垂直平分线∴ AB=AC∴ ∠B=∠C 例. 如果a、b、c是△ABC的三边(a≠b≠c),且满足 a4-b4+b2c2-a2c2=0,试判断三角形的形状。解:由题意得∵ a4-b4+b2c2-a2c2=0即又∵ a、b、c是△ABC的三边,且a≠b≠c∴即∴ △ABC是直角三角形 例. 如果△ABC的三边 AC=m2-n2, AB=2mn,BC=m2+n2 。求证:∠A=90。证明:由题意得∵ AC=m2-n2,AB=2mn,BC=m2+n2∴= (m2-n2)2+(2mn)2即∴ △ABC是直角三角形,边BC所对的角∠A=90。 如果△ABC的三边AC=n2-1,BC=2n,AB=n2+1。试判断△ABC是直角三角形,哪条边所对的角是直角?并说明理由。类型演练补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米;D、 60/13厘米;
CD直角三角形的判定方法:1、定义(角):有一个角是90°的三角形是直角三 角形。2、勾股定理的逆定理:如果三角形的三边长a、b、c(c为最大边)满足则,这个三角形是直角三角形作业布置(略)
