人教A版(2019)高中数学选择性必修第一册 《抛物线的简单几何性质---第二课时》名师课件(共27张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 《抛物线的简单几何性质---第二课时》名师课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 18:40:00 | ||
图片预览








文档简介
(共27张PPT)
复习引入
准线方程
焦点坐标
标准方程
图 形
问题:根据上表中抛物线的标准方程的不同形式与图形,焦点坐标,准线方程对应关系如何判断抛物线的焦点位置,开口方向?
1:一次项的变量如为,则轴为抛物线的对称轴,焦点就在对称轴轴上!
一次项的变量如为,则轴为抛物线的对称轴,焦点就在对称轴轴上!
2:一次变量的系数正负决定了开口方向
复习引入
焦点弦性质:抛物线的通径
抛物线,通过焦点而垂直于轴的弦叫做抛物线的通径,它的长为.
复习引入
焦点弦长公式
抛物线过焦点的弦与抛物线交于点,则焦点弦的长为
.
人教A版同步教材名师课件
抛物线的简单几何性质
---第二课时
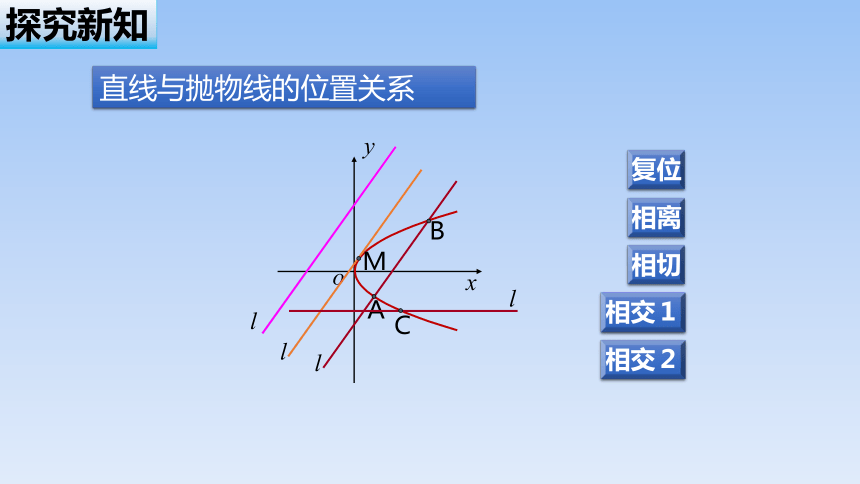
直线与抛物线的位置关系
探究新知
设直线:,抛物线,
直线与抛物线的交点个数等价于方程组解的个数,也等价于方程解的个数.
x
y
o
l
l
M
A
B
l
C
l
复位
相离
相切
相交1
相交2
探究新知
直线与抛物线的位置关系
探究新知
当时,直线和抛物线相交,有两个公共点;
当时,直线和抛物线相切,有一个公共点;
当时,直线和抛物线相离,无公共点.
(1)当时,
探究新知
(2)当时,
则直线与抛物线相交,有一个公共点.
特别地,当直线的斜率不存在时,设
则当与抛物线相交,有两个公共点;
当,与抛物线相切,有一个公共点;
当,与抛物线相离,无公共点.
解法一(公式法):根据已知条件写出直线方程,与抛物线方程联立方程组,求出坐标,两点间的距离公式或利用韦达定理(设坐标而不求坐标法)求出.
解法二(数形结合法):由右图集抛物线的定义可知:
所以
.
即只要求出即可求出.
典例讲解
例题1、斜率为的直线经过抛物线的焦点,且与抛物线相交于两点,求的长.
解析
∵,∴焦点准线.
则直线的方程为:,代入.
化简得:.
.
所以.
∴线段的长为.
典例讲解
例题1、斜率为的直线经过抛物线的焦点,且与抛物线相交于两点,求的长.
解析
设是过抛物线焦点的一条弦(焦点弦),若、则有.
特别地:当焦点弦垂直于轴时,抛物线的焦点弦长(即通径)
概念再现
焦点弦长公式
例2、过抛物线的焦点任作一条直线,交这抛物线于两点,求证:以为直径的圆和这抛物线的准线相切.
分析:运用抛物线的定义和平面几何知识来证比较简捷.
典例讲解
如图.设的中点为,过分别向准线引垂线,垂足为,
则
∴
所以是以为直径的圆的半径,且,
因而圆和准线相切.
典例讲解
例2、过抛物线的焦点任作一条直线,交这抛物线于两点,求证:以为直径的圆和这抛物线的准线相切.
证明
典例讲解
例题3、直线经过抛物线的焦点,且与抛物线相交于、两点,求证:
(1) (2) (3)求证:是钝角三角形
(1) ①当轴时, 所以.
②当轴不垂直时,设.
∵焦点.
∴直线的方程为:.
代入化简得:
∴
解析
典例讲解
例题3、直线经过抛物线的焦点,且与抛物线相交于、两点,求证:
(1) (2) (3)求证:是钝角三角形
(2)因为
所以
因为和异号,
所以.
解析
典例讲解
例题3、直线经过抛物线的焦点,且与抛物线相交于、两点,求证:
(1) (2) (3)求证:是钝角三角形
(3)因为
所以
.
所以是钝角三角形.
解析
典例讲解
例4、过抛物线的焦点任作一条直线,如果直线(倾斜角为)交这抛物线于两点.
(1)求弦长;(2)当时,求弦长;(3)求证:.
(1) 在中,
而,
得: ,
同理可得:
则: .
(即通径) .
.
解析
典例讲解
例5、已知过抛物线的焦点,斜率为的直线交抛物线于、两点,且.
(1)求该抛物线的方程;
(2)为坐标原点,为抛物线上一点,若,求的值.
(1)直线的方程是
与联立,从而有
所以.(2分)
由抛物线定义得: 所以,(4分)
所以抛物线方程为(6分)
解析
(2)由,化简得,
综上:或.(12分)
典例讲解
从而, , , ,(8分)
从而,.
设
又因为,即
即解得或.(10分)
(2)解决直线和抛物线的综合题方法很多,如斜率法、方程法、向量法、参数法等,解决这类问题的关键是代换和转化.
(1)直线与抛物线交点的个数,等价于直线方程、抛物线方程联立得到的方程组解的个数.注意直线斜率不存在和得到的方程二次项系数为的情况.
方法归纳
变式训练
(1)由得
因为直线与抛物线相切,
所以
解得
1.如图,直线与抛物线相切于点.
(1)求实数的值;
(2)求以点为圆心,且与抛物线的准线相切的圆的方程.
解析
变式训练
(2)由(1)可知,故方程为.
解得,代入,得,故点
因为圆与抛物线的准线相切,
所以圆的半径就等于圆心到抛物线的准线的距离,
即
所以圆的方程为
1.如图,直线与抛物线相切于点.
(1)求实数的值;
(2)求以点为圆心,且与抛物线的准线相切的圆的方程.
解析
变式训练
(1)由题意可设抛物线的方程为,
则由点在抛物线上,
得解得
故所求抛物线的方程是,
准线方程是
2.如图所示,抛物线关于轴对称,它的顶点为坐标原点,点
,均在抛物线上
(1)求抛物线的方程及其准线方程;
(2)当与的斜率存在且倾斜角互补时,证明:直线的斜率为定值.
解析
变式训练
(2)证明:因为与的斜率存在且倾斜角互补,
所以即
又,均在抛物线上,所以
从而有即
得
故直线的斜率
2.如图所示,抛物线关于轴对称,它的顶点为坐标原点,点
,均在抛物线上
(1)求抛物线的方程及其准线方程;
(2)当与的斜率存在且倾斜角互补时,证明:直线的斜率为定值.
解析
直线与抛物线的位置关系
素养提炼
设直线,抛物线,直线与抛物线的交点个数等价于方程组解的个数,
也等价于方程解的个数.
归纳小结
3.已知抛物线过焦点倾斜角为的直线交抛物线于,两点,则弦长称为焦点弦,其表达式为:
(1)焦半径
(2)
(3)(其中当是为通径: )
(强调:通径为焦点弦的最小值,是斜率不存在时的焦点弦长)
1.抛物线与直线的位置关系:
相交(一个或两个交点)、相切、相离.
判定方法:判别式法
2.抛物线几何性质:
顶点、开口、范围、对称性、离心率.
1、已知抛物线过点的直线交抛物线于两点.求证:.
2、过定点且与抛物线只有一个公共点的直线方程.
3、过抛物线的顶点做互相垂直的二弦.
(1)求中点的轨迹方程;
(2)证明:与轴的交点为定点.
作 业
复习引入
准线方程
焦点坐标
标准方程
图 形
问题:根据上表中抛物线的标准方程的不同形式与图形,焦点坐标,准线方程对应关系如何判断抛物线的焦点位置,开口方向?
1:一次项的变量如为,则轴为抛物线的对称轴,焦点就在对称轴轴上!
一次项的变量如为,则轴为抛物线的对称轴,焦点就在对称轴轴上!
2:一次变量的系数正负决定了开口方向
复习引入
焦点弦性质:抛物线的通径
抛物线,通过焦点而垂直于轴的弦叫做抛物线的通径,它的长为.
复习引入
焦点弦长公式
抛物线过焦点的弦与抛物线交于点,则焦点弦的长为
.
人教A版同步教材名师课件
抛物线的简单几何性质
---第二课时
直线与抛物线的位置关系
探究新知
设直线:,抛物线,
直线与抛物线的交点个数等价于方程组解的个数,也等价于方程解的个数.
x
y
o
l
l
M
A
B
l
C
l
复位
相离
相切
相交1
相交2
探究新知
直线与抛物线的位置关系
探究新知
当时,直线和抛物线相交,有两个公共点;
当时,直线和抛物线相切,有一个公共点;
当时,直线和抛物线相离,无公共点.
(1)当时,
探究新知
(2)当时,
则直线与抛物线相交,有一个公共点.
特别地,当直线的斜率不存在时,设
则当与抛物线相交,有两个公共点;
当,与抛物线相切,有一个公共点;
当,与抛物线相离,无公共点.
解法一(公式法):根据已知条件写出直线方程,与抛物线方程联立方程组,求出坐标,两点间的距离公式或利用韦达定理(设坐标而不求坐标法)求出.
解法二(数形结合法):由右图集抛物线的定义可知:
所以
.
即只要求出即可求出.
典例讲解
例题1、斜率为的直线经过抛物线的焦点,且与抛物线相交于两点,求的长.
解析
∵,∴焦点准线.
则直线的方程为:,代入.
化简得:.
.
所以.
∴线段的长为.
典例讲解
例题1、斜率为的直线经过抛物线的焦点,且与抛物线相交于两点,求的长.
解析
设是过抛物线焦点的一条弦(焦点弦),若、则有.
特别地:当焦点弦垂直于轴时,抛物线的焦点弦长(即通径)
概念再现
焦点弦长公式
例2、过抛物线的焦点任作一条直线,交这抛物线于两点,求证:以为直径的圆和这抛物线的准线相切.
分析:运用抛物线的定义和平面几何知识来证比较简捷.
典例讲解
如图.设的中点为,过分别向准线引垂线,垂足为,
则
∴
所以是以为直径的圆的半径,且,
因而圆和准线相切.
典例讲解
例2、过抛物线的焦点任作一条直线,交这抛物线于两点,求证:以为直径的圆和这抛物线的准线相切.
证明
典例讲解
例题3、直线经过抛物线的焦点,且与抛物线相交于、两点,求证:
(1) (2) (3)求证:是钝角三角形
(1) ①当轴时, 所以.
②当轴不垂直时,设.
∵焦点.
∴直线的方程为:.
代入化简得:
∴
解析
典例讲解
例题3、直线经过抛物线的焦点,且与抛物线相交于、两点,求证:
(1) (2) (3)求证:是钝角三角形
(2)因为
所以
因为和异号,
所以.
解析
典例讲解
例题3、直线经过抛物线的焦点,且与抛物线相交于、两点,求证:
(1) (2) (3)求证:是钝角三角形
(3)因为
所以
.
所以是钝角三角形.
解析
典例讲解
例4、过抛物线的焦点任作一条直线,如果直线(倾斜角为)交这抛物线于两点.
(1)求弦长;(2)当时,求弦长;(3)求证:.
(1) 在中,
而,
得: ,
同理可得:
则: .
(即通径) .
.
解析
典例讲解
例5、已知过抛物线的焦点,斜率为的直线交抛物线于、两点,且.
(1)求该抛物线的方程;
(2)为坐标原点,为抛物线上一点,若,求的值.
(1)直线的方程是
与联立,从而有
所以.(2分)
由抛物线定义得: 所以,(4分)
所以抛物线方程为(6分)
解析
(2)由,化简得,
综上:或.(12分)
典例讲解
从而, , , ,(8分)
从而,.
设
又因为,即
即解得或.(10分)
(2)解决直线和抛物线的综合题方法很多,如斜率法、方程法、向量法、参数法等,解决这类问题的关键是代换和转化.
(1)直线与抛物线交点的个数,等价于直线方程、抛物线方程联立得到的方程组解的个数.注意直线斜率不存在和得到的方程二次项系数为的情况.
方法归纳
变式训练
(1)由得
因为直线与抛物线相切,
所以
解得
1.如图,直线与抛物线相切于点.
(1)求实数的值;
(2)求以点为圆心,且与抛物线的准线相切的圆的方程.
解析
变式训练
(2)由(1)可知,故方程为.
解得,代入,得,故点
因为圆与抛物线的准线相切,
所以圆的半径就等于圆心到抛物线的准线的距离,
即
所以圆的方程为
1.如图,直线与抛物线相切于点.
(1)求实数的值;
(2)求以点为圆心,且与抛物线的准线相切的圆的方程.
解析
变式训练
(1)由题意可设抛物线的方程为,
则由点在抛物线上,
得解得
故所求抛物线的方程是,
准线方程是
2.如图所示,抛物线关于轴对称,它的顶点为坐标原点,点
,均在抛物线上
(1)求抛物线的方程及其准线方程;
(2)当与的斜率存在且倾斜角互补时,证明:直线的斜率为定值.
解析
变式训练
(2)证明:因为与的斜率存在且倾斜角互补,
所以即
又,均在抛物线上,所以
从而有即
得
故直线的斜率
2.如图所示,抛物线关于轴对称,它的顶点为坐标原点,点
,均在抛物线上
(1)求抛物线的方程及其准线方程;
(2)当与的斜率存在且倾斜角互补时,证明:直线的斜率为定值.
解析
直线与抛物线的位置关系
素养提炼
设直线,抛物线,直线与抛物线的交点个数等价于方程组解的个数,
也等价于方程解的个数.
归纳小结
3.已知抛物线过焦点倾斜角为的直线交抛物线于,两点,则弦长称为焦点弦,其表达式为:
(1)焦半径
(2)
(3)(其中当是为通径: )
(强调:通径为焦点弦的最小值,是斜率不存在时的焦点弦长)
1.抛物线与直线的位置关系:
相交(一个或两个交点)、相切、相离.
判定方法:判别式法
2.抛物线几何性质:
顶点、开口、范围、对称性、离心率.
1、已知抛物线过点的直线交抛物线于两点.求证:.
2、过定点且与抛物线只有一个公共点的直线方程.
3、过抛物线的顶点做互相垂直的二弦.
(1)求中点的轨迹方程;
(2)证明:与轴的交点为定点.
作 业
