人教A版(2019)高中数学选择性必修第一册 《抛物线的简单几何性质---第一课时》名师课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 《抛物线的简单几何性质---第一课时》名师课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 18:42:34 | ||
图片预览










文档简介
(共37张PPT)
抛物线的定义
l
F
K
M
H
平面内与一个定点和一条直线(点不在直线上)的距离相等的点的轨迹叫做抛物线.
点叫做抛物线的焦点,直线叫做抛物线的准线.
复习引入
图形 标准方程 焦点坐标 准线方程
复习引入
人教A版同步教材名师课件
抛物线的简单几何性质
---第一课时
学习目标
学 习 目 标 核心素养
抛物线的简单几何性质 直观想象
有关抛物线的计算、证明 数学运算
逻辑推理
直线与抛物线的位置关系 数学运算
逻辑推理
学习目标
学习目标:
1.掌握抛物线的几何性质.
2.掌握直线与抛物线的位置关系的判断及相关问题.
3.能利用方程及数形结合思想解决焦点弦、弦中点等问题.
学科核心素养:
1.通过抛物线几何性质的应用,培养学生的数学运算核心素养.
2.通过直线与抛物线的位置关系、焦点弦及中点弦、抛物线综合问题的学习,提升学生的逻辑推理、直观想象及数学运算的核心素养.
生活中存在着各种形式的抛物线
探究新知
类比椭圆、双曲线的几何性质,你认为可以讨论抛物线的哪些几何性质?
【思考】
探究新知
抛物线有许多重要性质.我们根据抛物线的标准方程
研究它的一些简单几何性质.
探究点:抛物线的简单几何性质
探究新知
(1)
当的值增大时,也增大,
这说明抛物线向右上方和右下方无限延伸.
由抛物线
所以抛物线的范围为
探究新知
而
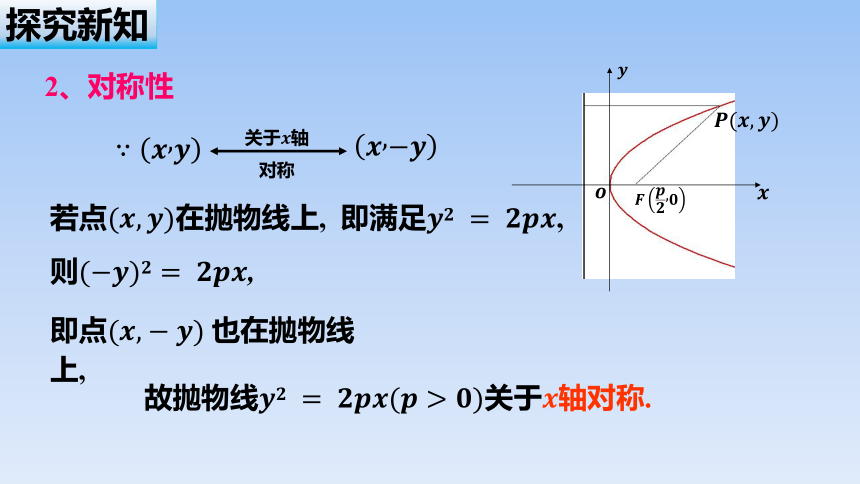
1、范围
关于轴
对称
即点也在抛物线上,
故抛物线关于轴对称.
则,
若点在抛物线上, 即满足,
探究新知
2、对称性
定义:抛物线与它的对称轴的交点叫做抛物线的顶点.
即:抛物线的顶点.
注:这与椭圆有四个顶点,双曲线有两个顶点不同.
探究新知
中,令,则.
3、顶点
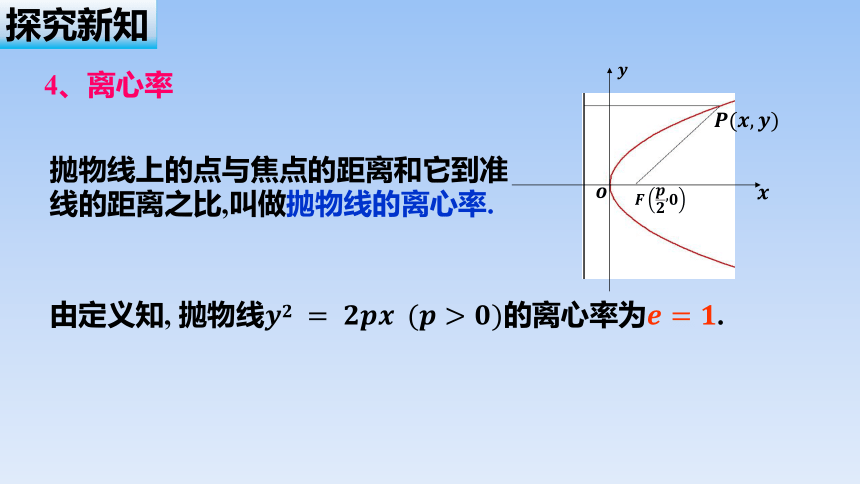
抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率.
由定义知, 抛物线的离心率为.
探究新知
4、离心率
【提升总结】
1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;
2.抛物线只有一条对称轴,没有对称中心;
3.抛物线只有一个顶点、一个焦点、一条准线;
4.抛物线的离心率是确定的,为;
思考:抛物线标准方程中的对抛物线开口的影响.
探究新知
过焦点而垂直于对称轴的弦AB,称为抛物线的通径.
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
越大,抛物线张口越大.
探究新知
5、通径
连接抛物线上任意一点与焦点的线段
叫做抛物线的焦半径.
焦半径公式:
探究新知
6、焦半径
探究新知
方程
图 形
范围
对称性
顶点
通径
焦半径
关于轴对称
关于轴对称
关于轴对称
关于轴对称
思考:若把“抛物线关于轴对称”改为“关于坐标轴对称”
典例讲解
例1、已知抛物线关于轴对称,它的顶点为坐标原点,并且经过点,求它的标准方程.
因为抛物线关于轴对称,它的顶点在坐标原点,并且经过点,
所以,可设它的标准方程为:
,
因为点在抛物线上,所以
即.
因此,所求抛物线的标准方程是
解析
法三、利用抛物线定义,数形结合求解.
法一、利用焦点坐标求出直线方程,联立方程组解出两点坐标;再利用两点间的距离公式即可.
法二、利用弦长公式.
典例讲解
例2、斜率为的直线经过抛物线的焦点,且与抛物线相交于两点,求线段的长.
分析
下面,我们介绍另外一种方法——数形结合的方法.
'
'
典例讲解
如图,设
由抛物线的定义可知,等于点A到准线的距离.
设,而,
于是
同理,
于是得
由此可见,只要求出点A,B的横坐标之和,
就可以求出.
'
'
典例讲解
由题意可知,
如图,设
到准线的距离分别为, .
由抛物线的定义可知,
.
由已知得抛物线的焦点为
所以直线的方程为. (1)
解析
典例讲解
将(1)代入化简得方程, 得,
于是
所以,线段
利用根与系数的关系可以直接求出.
方法指导:设而不求,列而不解.
解析
方法归纳
设过抛物线的焦点的弦的端点为,则,然后利用弦所在直线方程与抛物线方程联立、消元,由根与系数的关系求出即可.
过焦点的弦长的求解方法
变式训练
1.已知直线经过抛物线的焦点,且与抛物线相交于,两点.若直线的倾斜角为求的值.
因为直线的倾斜角为,
所以其斜率
又,所以直线的方程为
联立消去得
设,则,
而
所以.
解析
变式训练
2.若本例中“直线的倾斜角为”改为“”,求线段的中点到准线的距离.
设,由抛物线定义知
所以,
于是线段的中点的横坐标是.
又准线方程是,
所以点到准线的距离为.
解析
典例讲解
例3、已知抛物线.
(1)设点的坐标为(,0),求抛物线上距离点最近的点的坐标及相应的距离;
(2)设点的坐标为,求抛物线上的点到点的距离的最小值,并写出的函数表达式.
(1)由题意设抛物线上任一点的坐标为,
则
因为且在此区间上随着的增大而增大,
所以当时,
故距离点最近的点的坐标为,最短距离是
解析
典例讲解
(2)同(1)
求得
当,即时,
解得此时;
当,即时, ,
解得 此时.
所以
例3、已知抛物线.
(2)设点的坐标为,求抛物线上的点到点的距离的最小值,并写出的函数表达式.
解析
(2)利用抛物线的标准方程,进行消元代换,得到有关距离的含变量的代数式,以目标函数最值的求法解决.
解决与抛物线有关的最值问题的思路
求抛物线最值的常见题型是求抛物线上一点到定点的最值、求抛物线上一点到定直线的最值,解有关抛物线的最值问题主要有两种思路:
(1)利用抛物线的定义,进行到焦点的距离与到准线的距离的转化,数形结合,利用几何意义解决;
方法归纳
变式训练
3.如图,已知直线交抛物线于两点,试在抛物线这段曲线上求一点,使的面积最大,并求出这个最大面积.
由解得或
由图可知,,
则
设为抛物线这段曲线上一点,
为点到直线的距离,
解析
变式训练
则
因为
所以所以
从而当时,
因此,当点的坐标为时,
的面积取得最大值,最大值为.
3.如图,已知直线交抛物线于两点,试在抛物线这段曲线上求一点,使的面积最大,并求出这个最大面积.
解析
1.讨论抛物线的几何性质,一定要利用抛物线的标准方程;利用几何性质,也可以根据待定系数法求抛物线的方程.
2.直线与抛物线有一个交点,是直线与抛物线相切的必要不充分条件.
3.直线与抛物线的相交弦问题共有两类,一类是过焦点的弦,一类是不过焦点的弦.解决弦的问题,大多涉及抛物线的弦长、弦的中点、弦的斜率.常用的办法是将直线与抛物线联立,转化为关于或的一元二次方程,然后利用根与系数的关系,这样避免求交点.尤其是弦的中点问题,还应注意“点差法”的运用.
素养提炼
通径在反映抛物线开口大小上的作用
线段叫做抛物线的通径,长度为,越大,通径越大,即抛物线的开口越大;反之,越小,通径越小,即抛物线的开口越小.
说明:通径是所有焦点弦中最短的弦.
素养提炼
4.通径
通过抛物线的焦点作垂直于对称轴而交抛物线于两点的线段,称为抛物线的通径,如图所示.对于抛物线,由
可得,故抛物线的通径长为.
当堂练习
1.若抛物线上有两点且垂直于轴,若, 则抛物线的焦点到直线的距离为( )
线段所在的直线方程为,
抛物线的焦点坐标为,
则焦点到直线的距离为.
A
解析
2.在抛物线上到顶点与到焦点距离相等的点的坐标为( )
抛物线的顶点
焦点设符合题意,则有
所以符合题意的点为.
D
当堂练习
解析
当堂练习
3.设为坐标原点,为抛物线的焦点,是抛物线上一点,若,则点的坐标是( )
由题意知设
则由得
∴点的坐标为,故选.
B
解析
设,
由抛物线,可得
故的中点的纵坐标是
4.已知是过抛物线的焦点的弦,若,则的中点的纵坐标是____________.
当堂练习
解析
抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
抛物线的离心率是确定的,等于.
1. 范围:
抛物线只有一条对称轴,没有对称中心;
2. 对称性:
4. 离心率:
抛物线只有一个顶点,一个焦点,一条准线;
3. 顶点:
5.通径:
6.焦半径:
归纳小结
方法指导:设而不求,列而不解.
P138 练习:1、3、4
作 业
抛物线的定义
l
F
K
M
H
平面内与一个定点和一条直线(点不在直线上)的距离相等的点的轨迹叫做抛物线.
点叫做抛物线的焦点,直线叫做抛物线的准线.
复习引入
图形 标准方程 焦点坐标 准线方程
复习引入
人教A版同步教材名师课件
抛物线的简单几何性质
---第一课时
学习目标
学 习 目 标 核心素养
抛物线的简单几何性质 直观想象
有关抛物线的计算、证明 数学运算
逻辑推理
直线与抛物线的位置关系 数学运算
逻辑推理
学习目标
学习目标:
1.掌握抛物线的几何性质.
2.掌握直线与抛物线的位置关系的判断及相关问题.
3.能利用方程及数形结合思想解决焦点弦、弦中点等问题.
学科核心素养:
1.通过抛物线几何性质的应用,培养学生的数学运算核心素养.
2.通过直线与抛物线的位置关系、焦点弦及中点弦、抛物线综合问题的学习,提升学生的逻辑推理、直观想象及数学运算的核心素养.
生活中存在着各种形式的抛物线
探究新知
类比椭圆、双曲线的几何性质,你认为可以讨论抛物线的哪些几何性质?
【思考】
探究新知
抛物线有许多重要性质.我们根据抛物线的标准方程
研究它的一些简单几何性质.
探究点:抛物线的简单几何性质
探究新知
(1)
当的值增大时,也增大,
这说明抛物线向右上方和右下方无限延伸.
由抛物线
所以抛物线的范围为
探究新知
而
1、范围
关于轴
对称
即点也在抛物线上,
故抛物线关于轴对称.
则,
若点在抛物线上, 即满足,
探究新知
2、对称性
定义:抛物线与它的对称轴的交点叫做抛物线的顶点.
即:抛物线的顶点.
注:这与椭圆有四个顶点,双曲线有两个顶点不同.
探究新知
中,令,则.
3、顶点
抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率.
由定义知, 抛物线的离心率为.
探究新知
4、离心率
【提升总结】
1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;
2.抛物线只有一条对称轴,没有对称中心;
3.抛物线只有一个顶点、一个焦点、一条准线;
4.抛物线的离心率是确定的,为;
思考:抛物线标准方程中的对抛物线开口的影响.
探究新知
过焦点而垂直于对称轴的弦AB,称为抛物线的通径.
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
越大,抛物线张口越大.
探究新知
5、通径
连接抛物线上任意一点与焦点的线段
叫做抛物线的焦半径.
焦半径公式:
探究新知
6、焦半径
探究新知
方程
图 形
范围
对称性
顶点
通径
焦半径
关于轴对称
关于轴对称
关于轴对称
关于轴对称
思考:若把“抛物线关于轴对称”改为“关于坐标轴对称”
典例讲解
例1、已知抛物线关于轴对称,它的顶点为坐标原点,并且经过点,求它的标准方程.
因为抛物线关于轴对称,它的顶点在坐标原点,并且经过点,
所以,可设它的标准方程为:
,
因为点在抛物线上,所以
即.
因此,所求抛物线的标准方程是
解析
法三、利用抛物线定义,数形结合求解.
法一、利用焦点坐标求出直线方程,联立方程组解出两点坐标;再利用两点间的距离公式即可.
法二、利用弦长公式.
典例讲解
例2、斜率为的直线经过抛物线的焦点,且与抛物线相交于两点,求线段的长.
分析
下面,我们介绍另外一种方法——数形结合的方法.
'
'
典例讲解
如图,设
由抛物线的定义可知,等于点A到准线的距离.
设,而,
于是
同理,
于是得
由此可见,只要求出点A,B的横坐标之和,
就可以求出.
'
'
典例讲解
由题意可知,
如图,设
到准线的距离分别为, .
由抛物线的定义可知,
.
由已知得抛物线的焦点为
所以直线的方程为. (1)
解析
典例讲解
将(1)代入化简得方程, 得,
于是
所以,线段
利用根与系数的关系可以直接求出.
方法指导:设而不求,列而不解.
解析
方法归纳
设过抛物线的焦点的弦的端点为,则,然后利用弦所在直线方程与抛物线方程联立、消元,由根与系数的关系求出即可.
过焦点的弦长的求解方法
变式训练
1.已知直线经过抛物线的焦点,且与抛物线相交于,两点.若直线的倾斜角为求的值.
因为直线的倾斜角为,
所以其斜率
又,所以直线的方程为
联立消去得
设,则,
而
所以.
解析
变式训练
2.若本例中“直线的倾斜角为”改为“”,求线段的中点到准线的距离.
设,由抛物线定义知
所以,
于是线段的中点的横坐标是.
又准线方程是,
所以点到准线的距离为.
解析
典例讲解
例3、已知抛物线.
(1)设点的坐标为(,0),求抛物线上距离点最近的点的坐标及相应的距离;
(2)设点的坐标为,求抛物线上的点到点的距离的最小值,并写出的函数表达式.
(1)由题意设抛物线上任一点的坐标为,
则
因为且在此区间上随着的增大而增大,
所以当时,
故距离点最近的点的坐标为,最短距离是
解析
典例讲解
(2)同(1)
求得
当,即时,
解得此时;
当,即时, ,
解得 此时.
所以
例3、已知抛物线.
(2)设点的坐标为,求抛物线上的点到点的距离的最小值,并写出的函数表达式.
解析
(2)利用抛物线的标准方程,进行消元代换,得到有关距离的含变量的代数式,以目标函数最值的求法解决.
解决与抛物线有关的最值问题的思路
求抛物线最值的常见题型是求抛物线上一点到定点的最值、求抛物线上一点到定直线的最值,解有关抛物线的最值问题主要有两种思路:
(1)利用抛物线的定义,进行到焦点的距离与到准线的距离的转化,数形结合,利用几何意义解决;
方法归纳
变式训练
3.如图,已知直线交抛物线于两点,试在抛物线这段曲线上求一点,使的面积最大,并求出这个最大面积.
由解得或
由图可知,,
则
设为抛物线这段曲线上一点,
为点到直线的距离,
解析
变式训练
则
因为
所以所以
从而当时,
因此,当点的坐标为时,
的面积取得最大值,最大值为.
3.如图,已知直线交抛物线于两点,试在抛物线这段曲线上求一点,使的面积最大,并求出这个最大面积.
解析
1.讨论抛物线的几何性质,一定要利用抛物线的标准方程;利用几何性质,也可以根据待定系数法求抛物线的方程.
2.直线与抛物线有一个交点,是直线与抛物线相切的必要不充分条件.
3.直线与抛物线的相交弦问题共有两类,一类是过焦点的弦,一类是不过焦点的弦.解决弦的问题,大多涉及抛物线的弦长、弦的中点、弦的斜率.常用的办法是将直线与抛物线联立,转化为关于或的一元二次方程,然后利用根与系数的关系,这样避免求交点.尤其是弦的中点问题,还应注意“点差法”的运用.
素养提炼
通径在反映抛物线开口大小上的作用
线段叫做抛物线的通径,长度为,越大,通径越大,即抛物线的开口越大;反之,越小,通径越小,即抛物线的开口越小.
说明:通径是所有焦点弦中最短的弦.
素养提炼
4.通径
通过抛物线的焦点作垂直于对称轴而交抛物线于两点的线段,称为抛物线的通径,如图所示.对于抛物线,由
可得,故抛物线的通径长为.
当堂练习
1.若抛物线上有两点且垂直于轴,若, 则抛物线的焦点到直线的距离为( )
线段所在的直线方程为,
抛物线的焦点坐标为,
则焦点到直线的距离为.
A
解析
2.在抛物线上到顶点与到焦点距离相等的点的坐标为( )
抛物线的顶点
焦点设符合题意,则有
所以符合题意的点为.
D
当堂练习
解析
当堂练习
3.设为坐标原点,为抛物线的焦点,是抛物线上一点,若,则点的坐标是( )
由题意知设
则由得
∴点的坐标为,故选.
B
解析
设,
由抛物线,可得
故的中点的纵坐标是
4.已知是过抛物线的焦点的弦,若,则的中点的纵坐标是____________.
当堂练习
解析
抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
抛物线的离心率是确定的,等于.
1. 范围:
抛物线只有一条对称轴,没有对称中心;
2. 对称性:
4. 离心率:
抛物线只有一个顶点,一个焦点,一条准线;
3. 顶点:
5.通径:
6.焦半径:
归纳小结
方法指导:设而不求,列而不解.
P138 练习:1、3、4
作 业
