人教A版(2019)高中数学选择性必修第一册 素养评价:3.3.2抛物线的简单几何性质(含答案)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 素养评价:3.3.2抛物线的简单几何性质(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 510.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 18:57:45 | ||
图片预览




文档简介
二十七 抛物线的简单几何性质
(25分钟·50分)
一、选择题(每小题5分,共20分)
1.过抛物线C:y=x2的焦点F的直线交抛物线C于A,B两点,线段AB的中点为M,则|AB|= ( )
A. B. C.13 D.9
【加练·固】
已知F是抛物线x2=2y的焦点,A,B是抛物线上的两点,|AF|+|BF|=6,则线段AB的中点到x轴的距离为 .
2.设抛物线的焦点到顶点的距离为3,则抛物线上的点到准线的距离的取值范围是 ( )
A.(6,+∞) B.[6,+∞)
C.(3,+∞) D.[3,+∞)
3.从抛物线y2=4x在第一象限内的一点P引抛物线准线的垂线,垂足为M,且|PM|=4,设抛物线的焦点为F,则直线PF的斜率为 ( )
A. B. C. D.2
4.已知点M(4,y0)在抛物线C:y2=2px(p>0)上,点M到抛物线C的焦点F的距离为5,设O为坐标原点,则△OFM的面积为 ( )
A.1 B.2 C. D.2
二、填空题(每小题5分,共10分)
5.设抛物线y2=mx的准线与直线x=1的距离为3,则抛物线的方程为 .
6.抛物线y2=4x的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,当△FPM为等边三角形时,其面积为 .
三、解答题(每小题10分,共20分)
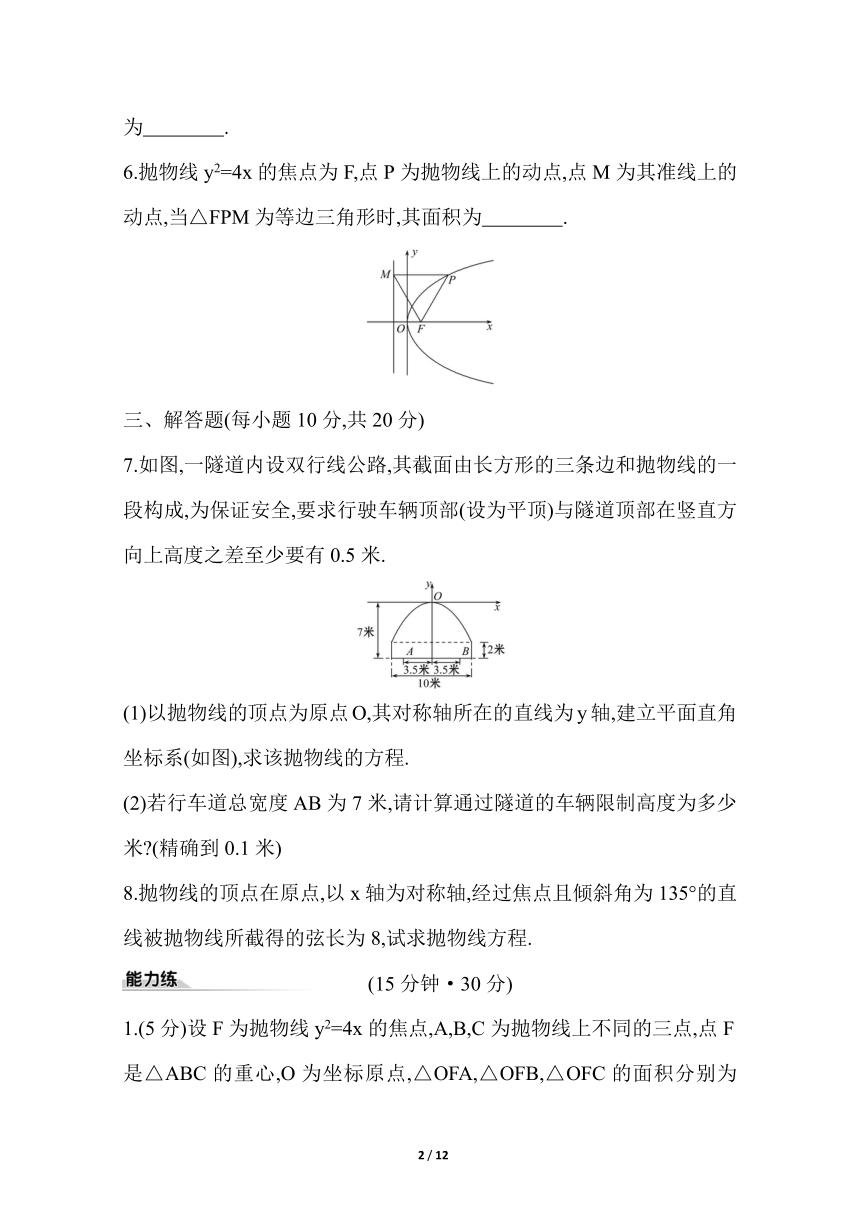
7.如图,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
(1)以抛物线的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系(如图),求该抛物线的方程.
(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米 (精确到0.1米)
8.抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线方程.
(15分钟·30分)
1.(5分)设F为抛物线y2=4x的焦点,A,B,C为抛物线上不同的三点,点F是△ABC的重心,O为坐标原点,△OFA,△OFB,△OFC的面积分别为S1,S2,S3,则++=( )
A.9 B.6 C.3 D.2
2.(5分)抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是 ( )
A. B. C. D.3
3.(5分)已知点P是抛物线y2=4x上的动点,点P在y轴上的射影是M,点A(4,6),则|PA|+|PM|的最小值是 .
4.(5分)如图:已知P为抛物线y2=4x上的动点,过P分别作y轴与直线x-y+4=0的垂线,垂足分别为A,B,则|PA|+|PB|的最小值为 .
5.(10分)点M(m,4)(m>0)为抛物线x2=2py(p>0)上一点,F为其焦点,已知|FM|=5.
(1)求m与p的值.
(2)以M点为切点作抛物线的切线,交y轴于点N,求△FMN的面积.
1.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足|PA|=m|PB|,当m取最大值时,点P恰好在以A,B为焦点的双曲线上,则该双曲线的离心率为 ( )
A. B. C.+1 D.-1
2.如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.
(1)若点C的纵坐标为2,求|MN|.
(2)若|AF|2=|AM|·|AN|,求圆C的半径.
二十七 抛物线的简单几何性质答案
(25分钟·50分)
一、选择题(每小题5分,共20分)
1.过抛物线C:y=x2的焦点F的直线交抛物线C于A,B两点,线段AB的中点为M,则|AB|= ( )
A. B. C.13 D.9
【解析】选D.由题意可得抛物线的标准形式为:x2=8y,所以准线方程为y=-2,
由题意可得A,B的纵坐标之和为×2=5,所以弦长|AB|=5+4=9.
【加练·固】
已知F是抛物线x2=2y的焦点,A,B是抛物线上的两点,|AF|+|BF|=6,则线段AB的中点到x轴的距离为 .
【解析】因为|AF|+|BF|=6,由抛物线的定义可得|AD|+|BE|=6,
又线段AB的中点到抛物线准线y=-的距离为(|AD|+|BE|)=3,所以线段AB的中点到x轴的距离为.
答案:
2.设抛物线的焦点到顶点的距离为3,则抛物线上的点到准线的距离的取值范围是 ( )
A.(6,+∞) B.[6,+∞)
C.(3,+∞) D.[3,+∞)
【解析】选D.因为抛物线的焦点到顶点的距离为3,所以=3,即p=6.又抛物线上的点到准线的距离的最小值为,所以抛物线上的点到准线的距离的取值范围为[3,+∞).
3.从抛物线y2=4x在第一象限内的一点P引抛物线准线的垂线,垂足为M,且|PM|=4,设抛物线的焦点为F,则直线PF的斜率为 ( )
A. B. C. D.2
【解析】选C.设P(x0,y0),依题意可知抛物线准线为x=-1,所以x0=4-1=3.
所以y0=2,所以P(3,2),F(1,0),
所以直线PF的斜率k==.
4.已知点M(4,y0)在抛物线C:y2=2px(p>0)上,点M到抛物线C的焦点F的距离为5,设O为坐标原点,则△OFM的面积为 ( )
A.1 B.2 C. D.2
【解析】选B.由题意得,抛物线的准线方程为:x=-,焦点F,
由抛物线的性质知点M到焦点的距离等于到准线的距离,
可得5=4+,
解得p=2,即抛物线的方程为y2=4x,
将M代入抛物线方程可得=16,
解得:|y0|=4,
所以S△OFM=|OF|·|y0|=×1×4=2.
二、填空题(每小题5分,共10分)
5.设抛物线y2=mx的准线与直线x=1的距离为3,则抛物线的方程为 .
【解析】当m>0时,准线方程为x=-=-2,所以m=8,此时抛物线方程为y2=8x,当m<0时,准线方程为x=-=4,所以m=-16,此时抛物线方程为y2=-16x,所以所求抛物线方程为y2=8x或y2=-16x.
答案:y2=8x或y2=-16x
6.抛物线y2=4x的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,当△FPM为等边三角形时,其面积为 .
【解析】据题意知,△PMF为等边三角形时,PF=PM,
所以PM垂直抛物线的准线,设P,
则M(-1,m),则等边三角形边长为1+,
因为F(1,0),所以由PM=FM,得1+=,
解得m2=12,所以等边三角形边长为4,其面积为4.
答案:4
三、解答题(每小题10分,共20分)
7.如图,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
(1)以抛物线的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系(如图),求该抛物线的方程.
(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米 (精确到0.1米)
【解析】(1)如图所示,
依题意,设该抛物线的方程为x2=-2py(p>0),
因为点C(5,-5)在抛物线上,
可解得p=,
所以该抛物线的方程为x2=-5y.
(2)设车辆高h米,
则|DB|=h+0.5,故D(3.5,h-6.5),代入方程x2=-5y,解得h=4.05,
所以车辆通过隧道的限制高度为4.0米.
8.抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线方程.
【解析】当抛物线的焦点在x轴正半轴上时,设抛物线方程为y2=2px(p>0),
焦点坐标为.因为直线过点且倾斜角为135°,
所以直线方程为y=-x+p.
设直线交抛物线于A(x1,y1),B(x2,y2),
则|AB|=x1+x2+p=8.①
由消去y,
得x2-3px+=0.
所以x1+x2=3p.②
由①②得p=2,所以所求抛物线方程为y2=4x.
当抛物线的焦点在x轴负半轴上时,同理可求得抛物线方程为y2=-4x.
综上,所求抛物线的方程为y2=4x或y2=-4x.
(15分钟·30分)
1.(5分)设F为抛物线y2=4x的焦点,A,B,C为抛物线上不同的三点,点F是△ABC的重心,O为坐标原点,△OFA,△OFB,△OFC的面积分别为S1,S2,S3,则++=( )
A.9 B.6 C.3 D.2
【解析】选C.设A,B,C三点的坐标分别为(x1,y1),(x2,y2),(x3,y3),
因为抛物线y2=4x的焦点F的坐标为(1,0),
所以S1=|y1|,S2=|y2|,S3=|y3|,
所以++=(++)=x1+x2+x3,
因为点F是△ABC的重心,
所以x1+x2+x3=3,
所以++=3.
2.(5分)抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是 ( )
A. B. C. D.3
【解析】选A.设抛物线y=-x2上一点M为(m,-m2),
该点到直线4x+3y-8=0的距离为,
当m=时,取得最小值为.
3.(5分)已知点P是抛物线y2=4x上的动点,点P在y轴上的射影是M,点A(4,6),则|PA|+|PM|的最小值是 .
【解析】如图,由y2=4x,得p=2,所以F(1,0),|PM|=|PF|-=|PF|-1,
所以|PA|+|PM|=|PA|+|PF|-1≥|AF|-1=-1=3-1.
答案:3-1
4.(5分)如图:已知P为抛物线y2=4x上的动点,过P分别作y轴与直线x-y+4=0的垂线,垂足分别为A,B,则|PA|+|PB|的最小值为 .
【解析】抛物线的准线方程是x=-1,
又根据抛物线的几何性质知,
抛物线上的点到焦点的距离等于其到准线的距离,
所以|PA|+|PB|=|PF|+|PB|-1,
|PF|+|PB|的最小值就是点F到直线x-y+4=0的距离,
所以点F到直线的距离d==,
即|PA|+|PB|的最小值是-1.
答案:-1
5.(10分)点M(m,4)(m>0)为抛物线x2=2py(p>0)上一点,F为其焦点,已知|FM|=5.
(1)求m与p的值.
(2)以M点为切点作抛物线的切线,交y轴于点N,求△FMN的面积.
【解析】(1)由抛物线定义知,|FM|=+4=5,
所以p=2.所以抛物线的方程为x2=4y,
又由M(m,4)在抛物线上,
所以m=4.故p=2,m=4.
(2)设过M点的切线方程为y-4=k(x-4),代入抛物线方程消去y得,x2-4kx+16k-16=0,
其判别式Δ=16k2-64(k-1)=0,
所以k=2,切线方程为y=2x-4,切线与y轴的交点为N(0,-4),抛物线的焦点F(0,1),
所以S△FMN=|FN|·m=×5×4=10.
1.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足|PA|=m|PB|,当m取最大值时,点P恰好在以A,B为焦点的双曲线上,则该双曲线的离心率为 ( )
A. B. C.+1 D.-1
【解析】选C.设点P(x,y),y≥0,
则m2===1+≤1+=2,当且仅当y=1时取等号,
此时点P(±2,1),2c=2,2a=|PA|-|PB|=2-2,e==+1.
2.如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.
(1)若点C的纵坐标为2,求|MN|.
(2)若|AF|2=|AM|·|AN|,求圆C的半径.
【解析】(1)抛物线y2=4x的准线l的方程为x=-1.
由点C的纵坐标为2,得点C的坐标为(1,2),
所以点C到准线l的距离d=2,
又|CO|=.所以|MN|=2=2=2.
(2)设C,则圆C的方程为+(y-y0)2=+,即x2-x+y2-2y0y=0.
由x=-1,得y2-2y0y+1+=0,
设M(-1,y1),N(-1,y2),则
由|AF|2=|AM|·|AN|,得|y1y2|=4,所以+1=4,
解得y0=±,此时Δ>0.
所以圆心C的坐标为或,
从而|CO|2=,|CO|=,即圆C的半径为.
PAGE
5 / 14
(25分钟·50分)
一、选择题(每小题5分,共20分)
1.过抛物线C:y=x2的焦点F的直线交抛物线C于A,B两点,线段AB的中点为M,则|AB|= ( )
A. B. C.13 D.9
【加练·固】
已知F是抛物线x2=2y的焦点,A,B是抛物线上的两点,|AF|+|BF|=6,则线段AB的中点到x轴的距离为 .
2.设抛物线的焦点到顶点的距离为3,则抛物线上的点到准线的距离的取值范围是 ( )
A.(6,+∞) B.[6,+∞)
C.(3,+∞) D.[3,+∞)
3.从抛物线y2=4x在第一象限内的一点P引抛物线准线的垂线,垂足为M,且|PM|=4,设抛物线的焦点为F,则直线PF的斜率为 ( )
A. B. C. D.2
4.已知点M(4,y0)在抛物线C:y2=2px(p>0)上,点M到抛物线C的焦点F的距离为5,设O为坐标原点,则△OFM的面积为 ( )
A.1 B.2 C. D.2
二、填空题(每小题5分,共10分)
5.设抛物线y2=mx的准线与直线x=1的距离为3,则抛物线的方程为 .
6.抛物线y2=4x的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,当△FPM为等边三角形时,其面积为 .
三、解答题(每小题10分,共20分)
7.如图,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
(1)以抛物线的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系(如图),求该抛物线的方程.
(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米 (精确到0.1米)
8.抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线方程.
(15分钟·30分)
1.(5分)设F为抛物线y2=4x的焦点,A,B,C为抛物线上不同的三点,点F是△ABC的重心,O为坐标原点,△OFA,△OFB,△OFC的面积分别为S1,S2,S3,则++=( )
A.9 B.6 C.3 D.2
2.(5分)抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是 ( )
A. B. C. D.3
3.(5分)已知点P是抛物线y2=4x上的动点,点P在y轴上的射影是M,点A(4,6),则|PA|+|PM|的最小值是 .
4.(5分)如图:已知P为抛物线y2=4x上的动点,过P分别作y轴与直线x-y+4=0的垂线,垂足分别为A,B,则|PA|+|PB|的最小值为 .
5.(10分)点M(m,4)(m>0)为抛物线x2=2py(p>0)上一点,F为其焦点,已知|FM|=5.
(1)求m与p的值.
(2)以M点为切点作抛物线的切线,交y轴于点N,求△FMN的面积.
1.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足|PA|=m|PB|,当m取最大值时,点P恰好在以A,B为焦点的双曲线上,则该双曲线的离心率为 ( )
A. B. C.+1 D.-1
2.如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.
(1)若点C的纵坐标为2,求|MN|.
(2)若|AF|2=|AM|·|AN|,求圆C的半径.
二十七 抛物线的简单几何性质答案
(25分钟·50分)
一、选择题(每小题5分,共20分)
1.过抛物线C:y=x2的焦点F的直线交抛物线C于A,B两点,线段AB的中点为M,则|AB|= ( )
A. B. C.13 D.9
【解析】选D.由题意可得抛物线的标准形式为:x2=8y,所以准线方程为y=-2,
由题意可得A,B的纵坐标之和为×2=5,所以弦长|AB|=5+4=9.
【加练·固】
已知F是抛物线x2=2y的焦点,A,B是抛物线上的两点,|AF|+|BF|=6,则线段AB的中点到x轴的距离为 .
【解析】因为|AF|+|BF|=6,由抛物线的定义可得|AD|+|BE|=6,
又线段AB的中点到抛物线准线y=-的距离为(|AD|+|BE|)=3,所以线段AB的中点到x轴的距离为.
答案:
2.设抛物线的焦点到顶点的距离为3,则抛物线上的点到准线的距离的取值范围是 ( )
A.(6,+∞) B.[6,+∞)
C.(3,+∞) D.[3,+∞)
【解析】选D.因为抛物线的焦点到顶点的距离为3,所以=3,即p=6.又抛物线上的点到准线的距离的最小值为,所以抛物线上的点到准线的距离的取值范围为[3,+∞).
3.从抛物线y2=4x在第一象限内的一点P引抛物线准线的垂线,垂足为M,且|PM|=4,设抛物线的焦点为F,则直线PF的斜率为 ( )
A. B. C. D.2
【解析】选C.设P(x0,y0),依题意可知抛物线准线为x=-1,所以x0=4-1=3.
所以y0=2,所以P(3,2),F(1,0),
所以直线PF的斜率k==.
4.已知点M(4,y0)在抛物线C:y2=2px(p>0)上,点M到抛物线C的焦点F的距离为5,设O为坐标原点,则△OFM的面积为 ( )
A.1 B.2 C. D.2
【解析】选B.由题意得,抛物线的准线方程为:x=-,焦点F,
由抛物线的性质知点M到焦点的距离等于到准线的距离,
可得5=4+,
解得p=2,即抛物线的方程为y2=4x,
将M代入抛物线方程可得=16,
解得:|y0|=4,
所以S△OFM=|OF|·|y0|=×1×4=2.
二、填空题(每小题5分,共10分)
5.设抛物线y2=mx的准线与直线x=1的距离为3,则抛物线的方程为 .
【解析】当m>0时,准线方程为x=-=-2,所以m=8,此时抛物线方程为y2=8x,当m<0时,准线方程为x=-=4,所以m=-16,此时抛物线方程为y2=-16x,所以所求抛物线方程为y2=8x或y2=-16x.
答案:y2=8x或y2=-16x
6.抛物线y2=4x的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,当△FPM为等边三角形时,其面积为 .
【解析】据题意知,△PMF为等边三角形时,PF=PM,
所以PM垂直抛物线的准线,设P,
则M(-1,m),则等边三角形边长为1+,
因为F(1,0),所以由PM=FM,得1+=,
解得m2=12,所以等边三角形边长为4,其面积为4.
答案:4
三、解答题(每小题10分,共20分)
7.如图,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
(1)以抛物线的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系(如图),求该抛物线的方程.
(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米 (精确到0.1米)
【解析】(1)如图所示,
依题意,设该抛物线的方程为x2=-2py(p>0),
因为点C(5,-5)在抛物线上,
可解得p=,
所以该抛物线的方程为x2=-5y.
(2)设车辆高h米,
则|DB|=h+0.5,故D(3.5,h-6.5),代入方程x2=-5y,解得h=4.05,
所以车辆通过隧道的限制高度为4.0米.
8.抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线方程.
【解析】当抛物线的焦点在x轴正半轴上时,设抛物线方程为y2=2px(p>0),
焦点坐标为.因为直线过点且倾斜角为135°,
所以直线方程为y=-x+p.
设直线交抛物线于A(x1,y1),B(x2,y2),
则|AB|=x1+x2+p=8.①
由消去y,
得x2-3px+=0.
所以x1+x2=3p.②
由①②得p=2,所以所求抛物线方程为y2=4x.
当抛物线的焦点在x轴负半轴上时,同理可求得抛物线方程为y2=-4x.
综上,所求抛物线的方程为y2=4x或y2=-4x.
(15分钟·30分)
1.(5分)设F为抛物线y2=4x的焦点,A,B,C为抛物线上不同的三点,点F是△ABC的重心,O为坐标原点,△OFA,△OFB,△OFC的面积分别为S1,S2,S3,则++=( )
A.9 B.6 C.3 D.2
【解析】选C.设A,B,C三点的坐标分别为(x1,y1),(x2,y2),(x3,y3),
因为抛物线y2=4x的焦点F的坐标为(1,0),
所以S1=|y1|,S2=|y2|,S3=|y3|,
所以++=(++)=x1+x2+x3,
因为点F是△ABC的重心,
所以x1+x2+x3=3,
所以++=3.
2.(5分)抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是 ( )
A. B. C. D.3
【解析】选A.设抛物线y=-x2上一点M为(m,-m2),
该点到直线4x+3y-8=0的距离为,
当m=时,取得最小值为.
3.(5分)已知点P是抛物线y2=4x上的动点,点P在y轴上的射影是M,点A(4,6),则|PA|+|PM|的最小值是 .
【解析】如图,由y2=4x,得p=2,所以F(1,0),|PM|=|PF|-=|PF|-1,
所以|PA|+|PM|=|PA|+|PF|-1≥|AF|-1=-1=3-1.
答案:3-1
4.(5分)如图:已知P为抛物线y2=4x上的动点,过P分别作y轴与直线x-y+4=0的垂线,垂足分别为A,B,则|PA|+|PB|的最小值为 .
【解析】抛物线的准线方程是x=-1,
又根据抛物线的几何性质知,
抛物线上的点到焦点的距离等于其到准线的距离,
所以|PA|+|PB|=|PF|+|PB|-1,
|PF|+|PB|的最小值就是点F到直线x-y+4=0的距离,
所以点F到直线的距离d==,
即|PA|+|PB|的最小值是-1.
答案:-1
5.(10分)点M(m,4)(m>0)为抛物线x2=2py(p>0)上一点,F为其焦点,已知|FM|=5.
(1)求m与p的值.
(2)以M点为切点作抛物线的切线,交y轴于点N,求△FMN的面积.
【解析】(1)由抛物线定义知,|FM|=+4=5,
所以p=2.所以抛物线的方程为x2=4y,
又由M(m,4)在抛物线上,
所以m=4.故p=2,m=4.
(2)设过M点的切线方程为y-4=k(x-4),代入抛物线方程消去y得,x2-4kx+16k-16=0,
其判别式Δ=16k2-64(k-1)=0,
所以k=2,切线方程为y=2x-4,切线与y轴的交点为N(0,-4),抛物线的焦点F(0,1),
所以S△FMN=|FN|·m=×5×4=10.
1.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足|PA|=m|PB|,当m取最大值时,点P恰好在以A,B为焦点的双曲线上,则该双曲线的离心率为 ( )
A. B. C.+1 D.-1
【解析】选C.设点P(x,y),y≥0,
则m2===1+≤1+=2,当且仅当y=1时取等号,
此时点P(±2,1),2c=2,2a=|PA|-|PB|=2-2,e==+1.
2.如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.
(1)若点C的纵坐标为2,求|MN|.
(2)若|AF|2=|AM|·|AN|,求圆C的半径.
【解析】(1)抛物线y2=4x的准线l的方程为x=-1.
由点C的纵坐标为2,得点C的坐标为(1,2),
所以点C到准线l的距离d=2,
又|CO|=.所以|MN|=2=2=2.
(2)设C,则圆C的方程为+(y-y0)2=+,即x2-x+y2-2y0y=0.
由x=-1,得y2-2y0y+1+=0,
设M(-1,y1),N(-1,y2),则
由|AF|2=|AM|·|AN|,得|y1y2|=4,所以+1=4,
解得y0=±,此时Δ>0.
所以圆心C的坐标为或,
从而|CO|2=,|CO|=,即圆C的半径为.
PAGE
5 / 14
