1.2.2 矩形的判定 课件 (共20张PPT)
文档属性
| 名称 | 1.2.2 矩形的判定 课件 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 22:06:55 | ||
图片预览






文档简介
(共20张PPT)
1.2.2 矩形的判定
北师大版九年级上册数学同步课件
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.
2. 能应用矩形的判定解决简单的证明题和计算题.
学习目标
重点
难点
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
新课引入
和小唯唯一起来学习吧
新知学习
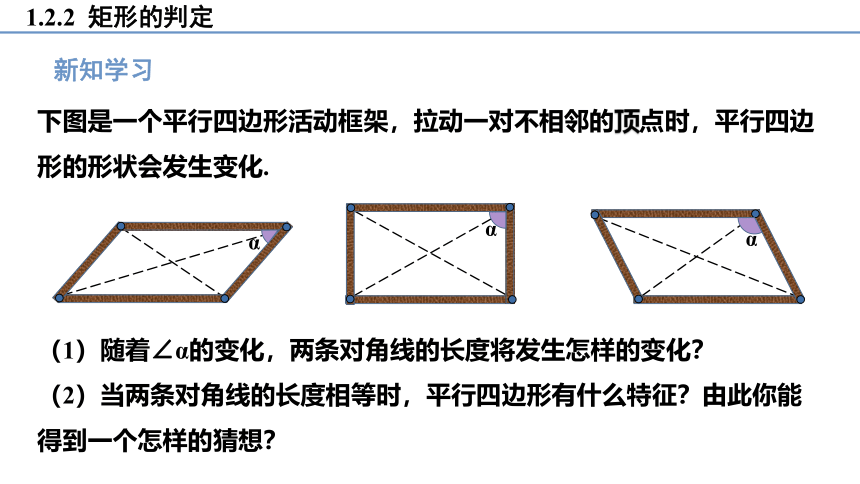
下图是一个平行四边形活动框架,拉动一对不相邻的顶点时,平行四边形的形状会发生变化.
α
α
α
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
(2)当两条对角线的长度相等时,平行四边形有什么特征?由此你能得到一个怎样的猜想?
探究
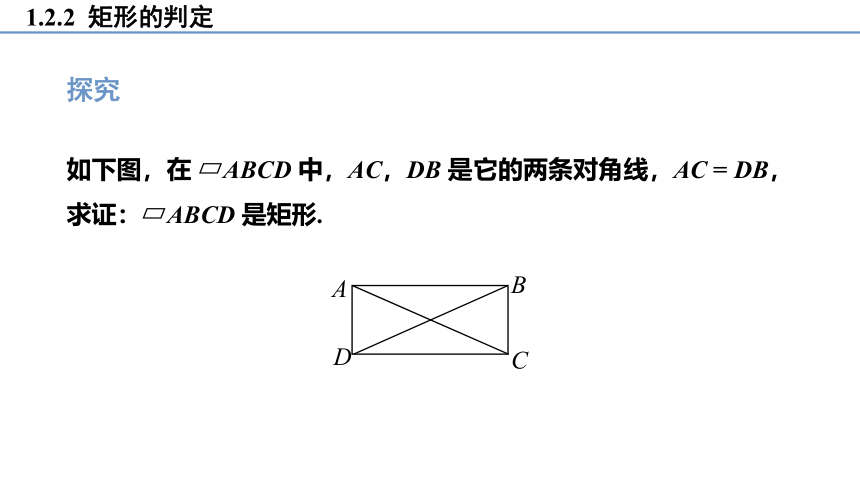
如下图,在 ABCD 中,AC,DB 是它的两条对角线,AC = DB,
求证: ABCD 是矩形.
A
B
C
D
证明:∵四边形 ABCD 是平行四边形,
∴AB = DC,AB∥DC.
又∵BC = CB,AC = DB,
∴ △ABC ≌ △DCB,
∴∠ABC =∠DCB.
∵AB∥CD,
∴∠ABC +∠DCB = 180°,
∴ ∠ABC =∠DCB = ×180° = 90°,
∴ ABCD 是矩形(矩形的定义).
A
B
C
D
归纳
定理:对角线相等的平行四边形是矩形.
A
B
C
D
在平行四边形 ABCD 中,
∵AC = BD,
∴平行四边形 ABCD 是矩形.
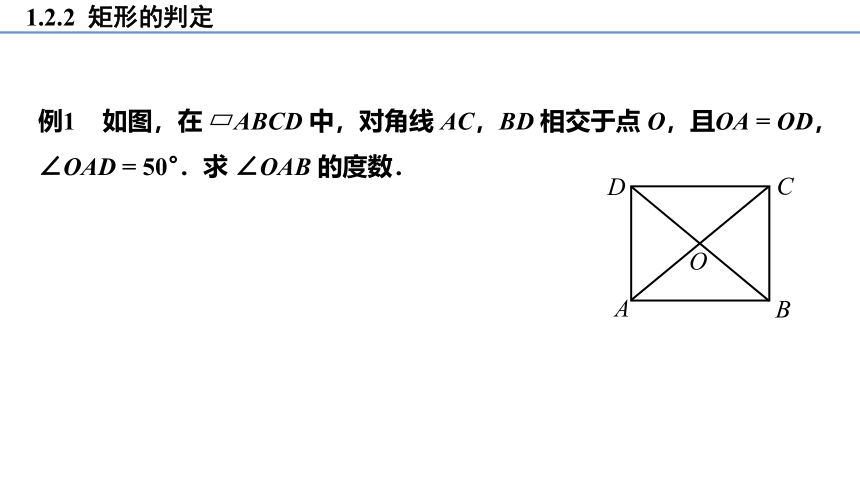
例1 如图,在 ABCD 中,对角线 AC,BD 相交于点 O,且OA = OD,∠OAD = 50°.求 ∠OAB 的度数.
A
B
C
D
O
解: ∵四边形 ABCD 是平行四边形,
∴OA = AC,OB = BD.
又∵OA = OD,
∴AC = BD,
∴四边形 ABCD 是矩形 ( 对角线相等的平行四边形是矩形 ),
∴∠BAD = 90° ( 矩形的四个角都是直角 ),
又∵∠OAD = 50°,
∴∠OAB = 90°-∠OAD = 40°.
A
B
C
D
O
思考
我们知道,矩形的四个角都是直角,反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形呢?
A
B
D
C
有一个角是直角
A
B
D
C
有二个角是直角
A
B
D
C
有三个角是直角
我猜测有三个角是直角的四边形是矩形.
探究
如图,在四边形 ABCD 中,∠A =∠B =∠C = 90°.
求证:四边形 ABCD 是矩形.
A
B
C
D
证明:∵∠A =∠B =∠C = 90°,
∴∠A +∠B = 180°,∠B +∠C = 180°,
∴AD∥BC,AB∥CD.
∴四边形 ABCD 是平行四边形,
∵∠A = 90°
∴四边形 ABCD 是矩形 ( 一个角是直角的平行四边形是矩形 ).
归纳
定理:有三个角是直角的四边形是矩形.
在四边形 ABCD 中,
∵ ∠A =∠B =∠C = 90°,
∴四边形 ABCD 是矩形.
A
B
C
D
1. 如图,在 ABCD 中,对角线 AC,BD 相交于点 O,△ABO 是等边三角形,AB = 4,求 ABCD 的面积.
A
B
C
D
O
60°
解:∵四边形 ABCD 是平行四边形,
∴OA = OC,OB = OD.
又∵△ABO 是等边三角形,
∴OA = OB = AB = 4.
针对训练
∴OA = OB = OC = OD = 4.
∴AC = BD = 2OA = 2×4 = 8.
∴ ABCD 是矩形 ( 对角线相等的平行四边形是矩形 ).
∴∠ABC = 90° ( 矩形的四个角都是直角 ).
在 Rt△ABC 中,BC = = = .
∴S ABCD = AB·BC = 4×4 = 16 .
A
B
C
D
O
60°
2. 如图, ABCD 的四个内角的平分线分别相交于 E、F、G、H,求证:四边形 EFGH 为矩形.
A
B
D
C
H
E
F
G
证明:在 ABCD 中,AD∥BC,
∴∠DAB +∠ABC = 180°.
∵AE 与 BG 分别为∠DAB、∠ABC 的平分线,
∴ ∠BAE+ ∠ABF = ∠DAB + ∠ABC = 90°.
∴∠AFB = 90°,即∠GFE = 90°.
同理可证∠AED =∠EHG = 90°,
∴四边形 EFGH 是矩形 ( 三个角是直角的四边形是矩形 ).
A
B
D
C
H
E
F
G
3. 如图,在△ABC 中,AB = AC,AD⊥BC,垂足为 D,AN 是△ABC 外角∠CAM 的平分线,CE⊥AN,垂足为 E,求证:四边形ADCE 为矩形.
自己试一试哦
∟
∟
证明:在△ABC 中,AB = AC,AD⊥BC,
∴∠DAC = ∠BAC ( 等腰三角形三线合一 ).
又∵AN 是△ABC 外角∠CAM 的平分线,
∴∠CAE= ∠CAM .
∴∠DAE =∠DAC+∠CAE = (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形 ADCE 为矩形 ( 三个角是直角的四边形是矩形 ).
课堂小结
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
定义
判定定理
1.2.2 矩形的判定
北师大版九年级上册数学同步课件
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.
2. 能应用矩形的判定解决简单的证明题和计算题.
学习目标
重点
难点
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
新课引入
和小唯唯一起来学习吧
新知学习
下图是一个平行四边形活动框架,拉动一对不相邻的顶点时,平行四边形的形状会发生变化.
α
α
α
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
(2)当两条对角线的长度相等时,平行四边形有什么特征?由此你能得到一个怎样的猜想?
探究
如下图,在 ABCD 中,AC,DB 是它的两条对角线,AC = DB,
求证: ABCD 是矩形.
A
B
C
D
证明:∵四边形 ABCD 是平行四边形,
∴AB = DC,AB∥DC.
又∵BC = CB,AC = DB,
∴ △ABC ≌ △DCB,
∴∠ABC =∠DCB.
∵AB∥CD,
∴∠ABC +∠DCB = 180°,
∴ ∠ABC =∠DCB = ×180° = 90°,
∴ ABCD 是矩形(矩形的定义).
A
B
C
D
归纳
定理:对角线相等的平行四边形是矩形.
A
B
C
D
在平行四边形 ABCD 中,
∵AC = BD,
∴平行四边形 ABCD 是矩形.
例1 如图,在 ABCD 中,对角线 AC,BD 相交于点 O,且OA = OD,∠OAD = 50°.求 ∠OAB 的度数.
A
B
C
D
O
解: ∵四边形 ABCD 是平行四边形,
∴OA = AC,OB = BD.
又∵OA = OD,
∴AC = BD,
∴四边形 ABCD 是矩形 ( 对角线相等的平行四边形是矩形 ),
∴∠BAD = 90° ( 矩形的四个角都是直角 ),
又∵∠OAD = 50°,
∴∠OAB = 90°-∠OAD = 40°.
A
B
C
D
O
思考
我们知道,矩形的四个角都是直角,反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形呢?
A
B
D
C
有一个角是直角
A
B
D
C
有二个角是直角
A
B
D
C
有三个角是直角
我猜测有三个角是直角的四边形是矩形.
探究
如图,在四边形 ABCD 中,∠A =∠B =∠C = 90°.
求证:四边形 ABCD 是矩形.
A
B
C
D
证明:∵∠A =∠B =∠C = 90°,
∴∠A +∠B = 180°,∠B +∠C = 180°,
∴AD∥BC,AB∥CD.
∴四边形 ABCD 是平行四边形,
∵∠A = 90°
∴四边形 ABCD 是矩形 ( 一个角是直角的平行四边形是矩形 ).
归纳
定理:有三个角是直角的四边形是矩形.
在四边形 ABCD 中,
∵ ∠A =∠B =∠C = 90°,
∴四边形 ABCD 是矩形.
A
B
C
D
1. 如图,在 ABCD 中,对角线 AC,BD 相交于点 O,△ABO 是等边三角形,AB = 4,求 ABCD 的面积.
A
B
C
D
O
60°
解:∵四边形 ABCD 是平行四边形,
∴OA = OC,OB = OD.
又∵△ABO 是等边三角形,
∴OA = OB = AB = 4.
针对训练
∴OA = OB = OC = OD = 4.
∴AC = BD = 2OA = 2×4 = 8.
∴ ABCD 是矩形 ( 对角线相等的平行四边形是矩形 ).
∴∠ABC = 90° ( 矩形的四个角都是直角 ).
在 Rt△ABC 中,BC = = = .
∴S ABCD = AB·BC = 4×4 = 16 .
A
B
C
D
O
60°
2. 如图, ABCD 的四个内角的平分线分别相交于 E、F、G、H,求证:四边形 EFGH 为矩形.
A
B
D
C
H
E
F
G
证明:在 ABCD 中,AD∥BC,
∴∠DAB +∠ABC = 180°.
∵AE 与 BG 分别为∠DAB、∠ABC 的平分线,
∴ ∠BAE+ ∠ABF = ∠DAB + ∠ABC = 90°.
∴∠AFB = 90°,即∠GFE = 90°.
同理可证∠AED =∠EHG = 90°,
∴四边形 EFGH 是矩形 ( 三个角是直角的四边形是矩形 ).
A
B
D
C
H
E
F
G
3. 如图,在△ABC 中,AB = AC,AD⊥BC,垂足为 D,AN 是△ABC 外角∠CAM 的平分线,CE⊥AN,垂足为 E,求证:四边形ADCE 为矩形.
自己试一试哦
∟
∟
证明:在△ABC 中,AB = AC,AD⊥BC,
∴∠DAC = ∠BAC ( 等腰三角形三线合一 ).
又∵AN 是△ABC 外角∠CAM 的平分线,
∴∠CAE= ∠CAM .
∴∠DAE =∠DAC+∠CAE = (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形 ADCE 为矩形 ( 三个角是直角的四边形是矩形 ).
课堂小结
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
定义
判定定理
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
