人教A版(2019)高中数学选择性必修第一册 高考模拟:圆锥曲线的方程(含解析)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 高考模拟:圆锥曲线的方程(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 171.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 00:00:00 | ||
图片预览





文档简介
高考模拟:圆锥曲线的方程
一、单项选择题
1.(2020·福建莆田第二十四中月考)“”是“曲线为双曲线”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
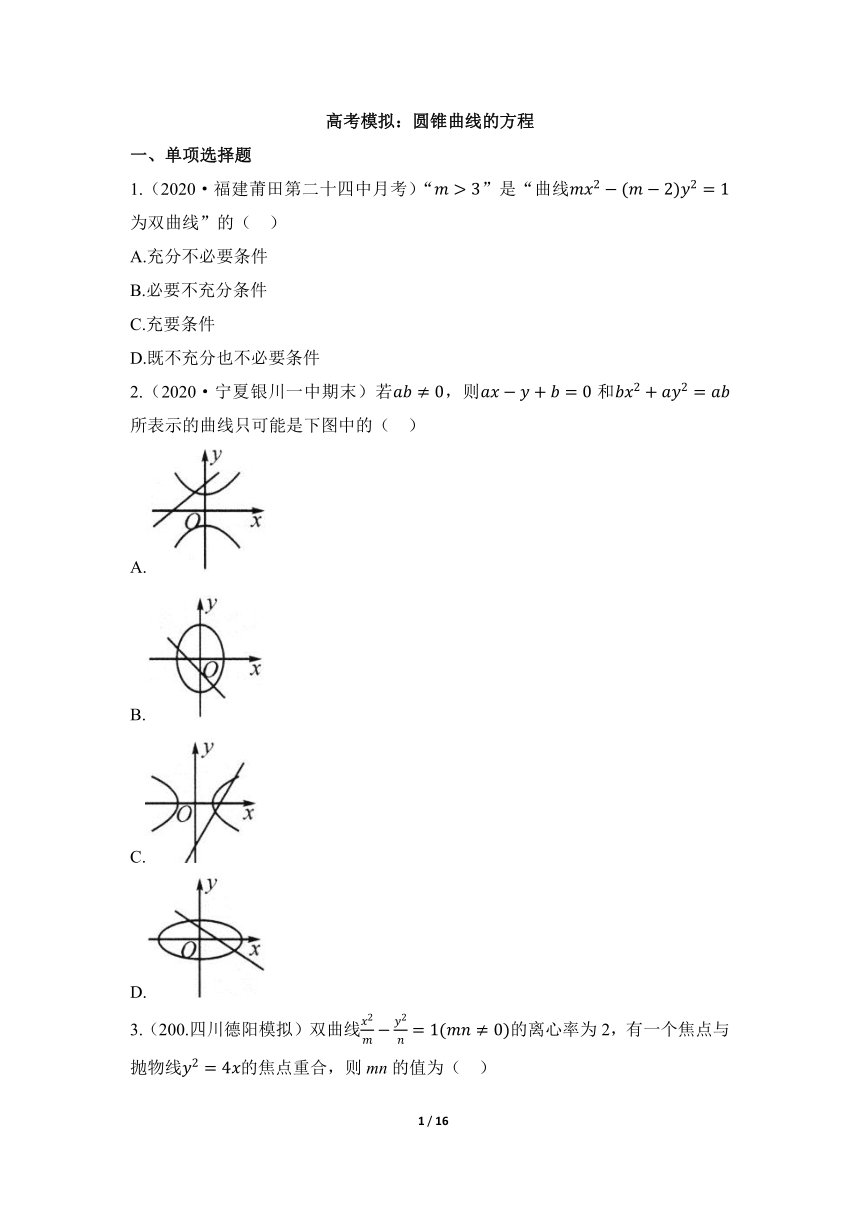
2.(2020·宁夏银川一中期末)若,则和所表示的曲线只可能是下图中的( )
A.
B.
C.
D.
3.(200.四川德阳模拟)双曲线的离心率为2,有一个焦点与抛物线的焦点重合,则mn的值为( )
A.
B.
C.
D.
4.(2020·江西南昌外国语学校月考)已知,椭圆的方程为,双曲线的方程为,若与的离心率之积为,则的渐近线方程为( )
A.
B.
C.
D.
5.(2020·福建厦门质检)设圆锥曲线T的两个焦点分别为。若曲线T上存在点P满足,则曲线T的离心率等于( )
A.或
B.或2
C.或2
D.或
6.(2020·湖北黄冈模拟)已知方程表示双曲线,且该双曲线两焦点之间的距离为4,则n的取值范围是( )
A.
B.
C.
D.
7.(2020·河北石家庄质检)已知双曲线的左、右焦点分别为,点M在双曲线的左支上,且,则此双曲线离心率的最大值为( )
A.
B.
C.2
D.
8.(2020·山东济南模拟)已知点,动圆C与直线MN相切于点B,过M,N与圆C相切的两直线相交于点P,则点P的轨迹方程为( )
A.
B.
C.
D.
二、多项选择题
9.已知椭圆的离心率为,点在椭圆C上,直线l平行于OM且在y轴上的截距为m,直线l与椭圆C交于A,B两个不同的点。下列结构正确的是( )
A.椭圆C的方程为
B.
C.
D.或
10.已知点P是双曲线的右支上一点,为双曲线E的左、右焦点,△的面积为20,则下列说法正确的是( )
A.点P的横坐标为
B.△的周长为
C.∠小于
D.△的内切圆半径为
11.已知抛物线的焦点为F,直线的斜率为且经过点F,直线l与抛物线C交于A,B两点(点A在第一象限),与抛物线的准线交于点D,若,则以下结论正确的是( )
A.
B.F为AD的中点
C.
D.
12.如图,已知椭圆,过抛物线焦点F的直线交抛物线于M,N两点,连接NO,MO并延长分别交于A,B两点,连接AB,△OMN与△OAB的面积分别记为,则在下列命题中,正确的是( )
A.若记直线NO,MO的斜率分别为,则的大小是定值为
B.△OAB的面积是定值1
C.线段OA,OB长度的平方和是定值5
D.设,则
三、填空题
13.(2020·河南新乡高三联考)设P为曲线上一点,,若,则_________。
14.(2020·湖南长沙调研)已知点,对于抛物线上任意一点Q,都满足,则a的取值范围是_________。
15.(2020·四川成都摸底测试)椭圆的左焦点为F,直线与椭圆相交于点M,N,当△FMN的周长最大时,△FMN的面积是_________。
16.(2020·湖北八校联考)我们把离心率为的双曲线称为黄金双曲线。如图是双曲线的图像,给出以下结论:
①双曲线是黄金双曲线;
②若,则该双曲线是黄金双曲线;
③若分别为左,右焦点,分别为左、右顶点,,且,则该双曲线是黄金双曲线;
④若直线MN过双曲线的右焦点,且,则该双曲线是黄金双曲线。
其中正确结论的序号为_______。(将所有正确结论的序号都填上)
四、解答题
17.(2020·湖北武汉外国语学校单元检测)(本小题满分10分)已知直线l过定点且斜率为k,试求k的范围,使得曲线的所有弦都不能被直线l垂直平分。
18.(2020·河南洛阳期中)(本小题满分12分)已知点,椭圆的离心率为是椭圆E的右焦点,直线AF的斜率为为坐标原点。
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程。
19.(2020·广东汕头模拟)(本小题满分12分)已知椭圆。
(1)求椭圆C的离心率;
(2)设O为原点,若点A在直线上,点B在椭圆C上,且,求线段AB长度的最小值。
20.(2020·河北九校高三第二次联考)(本小题满分12分)已知抛物线的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且。
(1)求抛物线C的方程
(2)设直线l为抛物线C的切线,且为l上一点,求的最小值。
21.(2020·湖南郴州模拟)(本小题满分12分)已知椭圆的离心率,坐标原点到直线的距离为。
(1)求椭圆的方程;
(2)若直线与椭圆相交于两点,是否存在实数k,使得以CD为直径的圆过点?若存在,求出k的值,若不存在,请说明理由。
22.(2020·湖北武汉4月调研)(本小题满分12分)已知椭圆,过点作倾斜角互补的两条不同直线,设与椭圆T交于A,B两点,与椭圆T交于C,D两点。
(1)若为线段AB的中点,求直线AB的方程;
(2)若直线与的斜率都存在,记,求的取值范围。
参考答案
1.
答案:A
解析:当时,,则原方程是双曲线方程;当原方程为双曲线方程时,有或。故“”是“曲线为双曲线”的充分不必要条件。故选A。
2.
答案:C
解析:且,
可化为可化为。
在A中,由直线得,由双曲线得,不合题意;
在B中,由直线得,由椭圆得,不合题意;
在C中,由直线得,由双曲线得,符合题意;
在D中,由直线得,由椭圆得,不合题意。故选C。
3.
答案:A
解析:因为抛物线的焦点为,故双曲线中,且①,又②,联立方程①②,解得。故。
4.
答案:C
解析:椭圆的离心率双曲线的离心率,由题意得,解得,所以,所以双曲线的渐近线方程为,即。
5.
答案:A
解析:设圆锥曲线的离心率为e,由,知①若圆锥曲线为椭圆,则由椭圆的定义,得;②若圆锥曲线为双曲线,则由双曲线的定义,得。综上,所求的离心率为或。故选A。
6.
答案:A
解析:若双曲线的焦点在x轴上,
则
又,
。
若双曲线的焦点在y轴上,则双曲线的标准方程为,即
即,且,此时n不存在,故选A。
7.
答案:A
解析:因为,所以,即,故,则,当且仅当M为双曲线的左顶点时,等号成立。故此双曲线离心率的最大值为。
8.
答案:A
解析:设圆与直线PM,PN分别相切于E,F,则。
点P的轨迹是以为焦点的双曲线的右支,且。故双曲线的方程是。
9.
答案:ABC
解析:由题意,得解得故椭圆C的方程为,A项正确;由于,故B项正确;因为直线l的斜率,又l在y轴上的截距为m,所以l的方程为。由得。因为直线l与椭圆C交于A,B两个不同的点,所以,解得,故C项正确,D项错误。
10.
答案:ABCD
解析:双曲线的,不妨设,由
△的面积为20,可得,即。由,可得,故A项正确。由,且,可得,则,则,故C项正确:由,则△的周长为,故B项正确。设△的内切圆半径为r,可得,可得,解得,数D项正确,故选A、B、C、D。
11.
答案:ABC
解析:如图,,直线l的斜率为,则直线方程为,联立得,解得。
由,得,所以抛物线方程为。,则,所以,则F为AD的中点。故选A、B、C。
12.
答案:ABCD
解析:,设直线MN的方程为,联立方程组消元得,所以,所以,所以:故A项正确;设直线OA的方程为,则直线0B的方程为,联立方程组解得,不妨设A在第三象限,则,用替换m可得,所以A到OB的距离,又,所以,故B项正确;又,所以,故C项正确;联方方程组可得,故,所以替换m可得所以M到直线OA的距离,所以4m2=2m+≥2,当且仅当即时取等号,所以,故D项正确。故选A、B、C、D。
13.
答案:4
解析:由,得,即,故P为双曲线右支上一点,且A,B分别为该双曲线的左、右焦点,则,故。
14.
答案:
解析:设,由得,即,所以,所以恒成立,则,即。故填。
15.
答案:
解析:如图,设右焦点为,连接,
因为△FMN的周长,且,当三点共线,即时,等号成立,所以当△FMN的周长最大时,,所以△FMN的面积。
16.
答案:①②③④
解析:对于①,,则,则,所以,所以双曲线是黄金双曲线,故①正确;对于②,,整理得,解得(负值舍去),所以双曲线是黄金双曲线,故②正确;对于③,,又在Rt△中,,故,整理得,由②可知,所以双曲线是黄金双曲线,故③正确;对于④,易知,把代入双曲线的方程得,解得,则。因为,所以由对称关系知△MON为等腰直角三角形,所以,所以△为等腰直角三角形,所以,即,由②可知,所以双曲线是黄金双曲线,故④正确。
17.
答案:见解析
解析:当时,符合题意。当时,设直线l的方程为,设被l垂直平分的弦的两端点为,则BC的中点为,
若BC被l垂直平分,则且,
从而,
即,解得。
再用补集思想,故即为所求。
18.
答案:见解析
解析:(1)设,由条件知,
解得。
又,所以,则,
故E的方程为。
(2)当轴时不合题意,故设,。
将代入,
得。
当,即时,
从而。
又点O到直线PQ的距离。
所以△的面积,设,设,则,
因为,当且仅当即,即时等号成立,满足,所以当△OPQ的面积取得最大值时,直线l的方程为或。
19.
答案:见解析
解析:(1)由题意,得椭圆C的标准方程为,
所以,从而。
因此。
故椭圆C的离心率。
(2)设点A,B的坐标分别为,其中,。
因为,所以,即,解得。
又,所以
。
因为,当且仅当时等号成立,
所以。
故线段AB长度的最小值为。
20.
答案:见解析
解析:(1)由题意可知,则直线MN的方程为,
代入中,得,设,则有,
,即,解得,
抛物线C的方程为。
(2)设直线l的方程为,代入,得。
直线l为抛物线C的切线,,解得。
由(1)可知,,
设,则,
,
又,
,
故,
当且仅当,即点P的坐标为时,取得最小值。
21.
答案:见解析
解析:(1)由点到直线的距离公式得。
椭圆的离心率,
椭圆的方程是。
(2)联立直线与椭圆的方程,得消去y,得,
,
或。
设,则有。
。
若以CD为直径的圆过点E,则,即,
。
又,
,
,
解得,
当时,以CD为直径的圆过点E。
22.
答案:见解析
解析:(1)方法一(点差法):由题意可知直线AB的斜率存在。
设,则
两式作差得,
直线AB的方程为,即。
方法二:由题意可知直线AB的斜率存在。
设直线AB的斜率为k,
则其方程为,代入中,
得。
。
。
设,则
的中点为,
,则。
直线AB的方程为,即。
(2)由(1)可知
。
设直线CD的方程为。
同理可得。
。
。
令,则,
令,
在上单调递减,
或。
故或。
。
【点评】(1)方法一:利用点差法得直线AB的斜率,进而求得直线AB的方程。
方法二:设出直线AB的方程,与椭圆方程联立并消元,利用根与系数的关系及AB中点的坐标建立斜率k的方程,从而求得k,得到直线AB的方程。
(2)利用弦长公式求得与,进而将表示成关于k的函数,结合函数特征及函数性质求得的取值范围。
7 / 9
一、单项选择题
1.(2020·福建莆田第二十四中月考)“”是“曲线为双曲线”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.(2020·宁夏银川一中期末)若,则和所表示的曲线只可能是下图中的( )
A.
B.
C.
D.
3.(200.四川德阳模拟)双曲线的离心率为2,有一个焦点与抛物线的焦点重合,则mn的值为( )
A.
B.
C.
D.
4.(2020·江西南昌外国语学校月考)已知,椭圆的方程为,双曲线的方程为,若与的离心率之积为,则的渐近线方程为( )
A.
B.
C.
D.
5.(2020·福建厦门质检)设圆锥曲线T的两个焦点分别为。若曲线T上存在点P满足,则曲线T的离心率等于( )
A.或
B.或2
C.或2
D.或
6.(2020·湖北黄冈模拟)已知方程表示双曲线,且该双曲线两焦点之间的距离为4,则n的取值范围是( )
A.
B.
C.
D.
7.(2020·河北石家庄质检)已知双曲线的左、右焦点分别为,点M在双曲线的左支上,且,则此双曲线离心率的最大值为( )
A.
B.
C.2
D.
8.(2020·山东济南模拟)已知点,动圆C与直线MN相切于点B,过M,N与圆C相切的两直线相交于点P,则点P的轨迹方程为( )
A.
B.
C.
D.
二、多项选择题
9.已知椭圆的离心率为,点在椭圆C上,直线l平行于OM且在y轴上的截距为m,直线l与椭圆C交于A,B两个不同的点。下列结构正确的是( )
A.椭圆C的方程为
B.
C.
D.或
10.已知点P是双曲线的右支上一点,为双曲线E的左、右焦点,△的面积为20,则下列说法正确的是( )
A.点P的横坐标为
B.△的周长为
C.∠小于
D.△的内切圆半径为
11.已知抛物线的焦点为F,直线的斜率为且经过点F,直线l与抛物线C交于A,B两点(点A在第一象限),与抛物线的准线交于点D,若,则以下结论正确的是( )
A.
B.F为AD的中点
C.
D.
12.如图,已知椭圆,过抛物线焦点F的直线交抛物线于M,N两点,连接NO,MO并延长分别交于A,B两点,连接AB,△OMN与△OAB的面积分别记为,则在下列命题中,正确的是( )
A.若记直线NO,MO的斜率分别为,则的大小是定值为
B.△OAB的面积是定值1
C.线段OA,OB长度的平方和是定值5
D.设,则
三、填空题
13.(2020·河南新乡高三联考)设P为曲线上一点,,若,则_________。
14.(2020·湖南长沙调研)已知点,对于抛物线上任意一点Q,都满足,则a的取值范围是_________。
15.(2020·四川成都摸底测试)椭圆的左焦点为F,直线与椭圆相交于点M,N,当△FMN的周长最大时,△FMN的面积是_________。
16.(2020·湖北八校联考)我们把离心率为的双曲线称为黄金双曲线。如图是双曲线的图像,给出以下结论:
①双曲线是黄金双曲线;
②若,则该双曲线是黄金双曲线;
③若分别为左,右焦点,分别为左、右顶点,,且,则该双曲线是黄金双曲线;
④若直线MN过双曲线的右焦点,且,则该双曲线是黄金双曲线。
其中正确结论的序号为_______。(将所有正确结论的序号都填上)
四、解答题
17.(2020·湖北武汉外国语学校单元检测)(本小题满分10分)已知直线l过定点且斜率为k,试求k的范围,使得曲线的所有弦都不能被直线l垂直平分。
18.(2020·河南洛阳期中)(本小题满分12分)已知点,椭圆的离心率为是椭圆E的右焦点,直线AF的斜率为为坐标原点。
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程。
19.(2020·广东汕头模拟)(本小题满分12分)已知椭圆。
(1)求椭圆C的离心率;
(2)设O为原点,若点A在直线上,点B在椭圆C上,且,求线段AB长度的最小值。
20.(2020·河北九校高三第二次联考)(本小题满分12分)已知抛物线的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且。
(1)求抛物线C的方程
(2)设直线l为抛物线C的切线,且为l上一点,求的最小值。
21.(2020·湖南郴州模拟)(本小题满分12分)已知椭圆的离心率,坐标原点到直线的距离为。
(1)求椭圆的方程;
(2)若直线与椭圆相交于两点,是否存在实数k,使得以CD为直径的圆过点?若存在,求出k的值,若不存在,请说明理由。
22.(2020·湖北武汉4月调研)(本小题满分12分)已知椭圆,过点作倾斜角互补的两条不同直线,设与椭圆T交于A,B两点,与椭圆T交于C,D两点。
(1)若为线段AB的中点,求直线AB的方程;
(2)若直线与的斜率都存在,记,求的取值范围。
参考答案
1.
答案:A
解析:当时,,则原方程是双曲线方程;当原方程为双曲线方程时,有或。故“”是“曲线为双曲线”的充分不必要条件。故选A。
2.
答案:C
解析:且,
可化为可化为。
在A中,由直线得,由双曲线得,不合题意;
在B中,由直线得,由椭圆得,不合题意;
在C中,由直线得,由双曲线得,符合题意;
在D中,由直线得,由椭圆得,不合题意。故选C。
3.
答案:A
解析:因为抛物线的焦点为,故双曲线中,且①,又②,联立方程①②,解得。故。
4.
答案:C
解析:椭圆的离心率双曲线的离心率,由题意得,解得,所以,所以双曲线的渐近线方程为,即。
5.
答案:A
解析:设圆锥曲线的离心率为e,由,知①若圆锥曲线为椭圆,则由椭圆的定义,得;②若圆锥曲线为双曲线,则由双曲线的定义,得。综上,所求的离心率为或。故选A。
6.
答案:A
解析:若双曲线的焦点在x轴上,
则
又,
。
若双曲线的焦点在y轴上,则双曲线的标准方程为,即
即,且,此时n不存在,故选A。
7.
答案:A
解析:因为,所以,即,故,则,当且仅当M为双曲线的左顶点时,等号成立。故此双曲线离心率的最大值为。
8.
答案:A
解析:设圆与直线PM,PN分别相切于E,F,则。
点P的轨迹是以为焦点的双曲线的右支,且。故双曲线的方程是。
9.
答案:ABC
解析:由题意,得解得故椭圆C的方程为,A项正确;由于,故B项正确;因为直线l的斜率,又l在y轴上的截距为m,所以l的方程为。由得。因为直线l与椭圆C交于A,B两个不同的点,所以,解得,故C项正确,D项错误。
10.
答案:ABCD
解析:双曲线的,不妨设,由
△的面积为20,可得,即。由,可得,故A项正确。由,且,可得,则,则,故C项正确:由,则△的周长为,故B项正确。设△的内切圆半径为r,可得,可得,解得,数D项正确,故选A、B、C、D。
11.
答案:ABC
解析:如图,,直线l的斜率为,则直线方程为,联立得,解得。
由,得,所以抛物线方程为。,则,所以,则F为AD的中点。故选A、B、C。
12.
答案:ABCD
解析:,设直线MN的方程为,联立方程组消元得,所以,所以,所以:故A项正确;设直线OA的方程为,则直线0B的方程为,联立方程组解得,不妨设A在第三象限,则,用替换m可得,所以A到OB的距离,又,所以,故B项正确;又,所以,故C项正确;联方方程组可得,故,所以替换m可得所以M到直线OA的距离,所以4m2=2m+≥2,当且仅当即时取等号,所以,故D项正确。故选A、B、C、D。
13.
答案:4
解析:由,得,即,故P为双曲线右支上一点,且A,B分别为该双曲线的左、右焦点,则,故。
14.
答案:
解析:设,由得,即,所以,所以恒成立,则,即。故填。
15.
答案:
解析:如图,设右焦点为,连接,
因为△FMN的周长,且,当三点共线,即时,等号成立,所以当△FMN的周长最大时,,所以△FMN的面积。
16.
答案:①②③④
解析:对于①,,则,则,所以,所以双曲线是黄金双曲线,故①正确;对于②,,整理得,解得(负值舍去),所以双曲线是黄金双曲线,故②正确;对于③,,又在Rt△中,,故,整理得,由②可知,所以双曲线是黄金双曲线,故③正确;对于④,易知,把代入双曲线的方程得,解得,则。因为,所以由对称关系知△MON为等腰直角三角形,所以,所以△为等腰直角三角形,所以,即,由②可知,所以双曲线是黄金双曲线,故④正确。
17.
答案:见解析
解析:当时,符合题意。当时,设直线l的方程为,设被l垂直平分的弦的两端点为,则BC的中点为,
若BC被l垂直平分,则且,
从而,
即,解得。
再用补集思想,故即为所求。
18.
答案:见解析
解析:(1)设,由条件知,
解得。
又,所以,则,
故E的方程为。
(2)当轴时不合题意,故设,。
将代入,
得。
当,即时,
从而。
又点O到直线PQ的距离。
所以△的面积,设,设,则,
因为,当且仅当即,即时等号成立,满足,所以当△OPQ的面积取得最大值时,直线l的方程为或。
19.
答案:见解析
解析:(1)由题意,得椭圆C的标准方程为,
所以,从而。
因此。
故椭圆C的离心率。
(2)设点A,B的坐标分别为,其中,。
因为,所以,即,解得。
又,所以
。
因为,当且仅当时等号成立,
所以。
故线段AB长度的最小值为。
20.
答案:见解析
解析:(1)由题意可知,则直线MN的方程为,
代入中,得,设,则有,
,即,解得,
抛物线C的方程为。
(2)设直线l的方程为,代入,得。
直线l为抛物线C的切线,,解得。
由(1)可知,,
设,则,
,
又,
,
故,
当且仅当,即点P的坐标为时,取得最小值。
21.
答案:见解析
解析:(1)由点到直线的距离公式得。
椭圆的离心率,
椭圆的方程是。
(2)联立直线与椭圆的方程,得消去y,得,
,
或。
设,则有。
。
若以CD为直径的圆过点E,则,即,
。
又,
,
,
解得,
当时,以CD为直径的圆过点E。
22.
答案:见解析
解析:(1)方法一(点差法):由题意可知直线AB的斜率存在。
设,则
两式作差得,
直线AB的方程为,即。
方法二:由题意可知直线AB的斜率存在。
设直线AB的斜率为k,
则其方程为,代入中,
得。
。
。
设,则
的中点为,
,则。
直线AB的方程为,即。
(2)由(1)可知
。
设直线CD的方程为。
同理可得。
。
。
令,则,
令,
在上单调递减,
或。
故或。
。
【点评】(1)方法一:利用点差法得直线AB的斜率,进而求得直线AB的方程。
方法二:设出直线AB的方程,与椭圆方程联立并消元,利用根与系数的关系及AB中点的坐标建立斜率k的方程,从而求得k,得到直线AB的方程。
(2)利用弦长公式求得与,进而将表示成关于k的函数,结合函数特征及函数性质求得的取值范围。
7 / 9
