5.5.2简单的三角恒等变换 人教A版(2019)必修第一册高中数学精品课件(共23张PPT)
文档属性
| 名称 | 5.5.2简单的三角恒等变换 人教A版(2019)必修第一册高中数学精品课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 915.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 08:39:22 | ||
图片预览








文档简介
(共23张PPT)
5.5 三角恒等变换
必修一第五章
5.5.2 简单的三角恒等变换
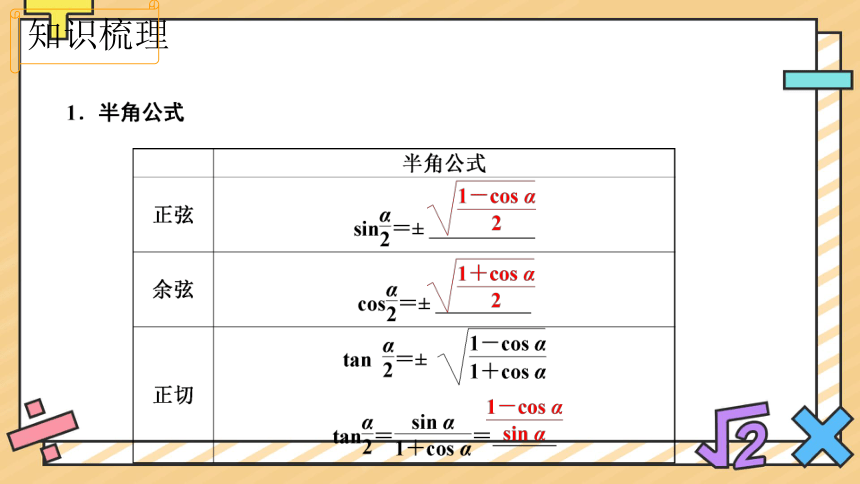
知识梳理
知识梳理
知识梳理
知识梳理
例题解析
例题解析
例题解析
例2.化简:(0).
解:原式
∵0,∴
∴
∴原式
例题解析
B
例题解析
例题解析
例题解析
例题解析
例题解析
例6.(1)求证:;
(2)
证:(1)左边右边.
(2)左边
右边.
例题解析
例题解析
例题解析
例8.求下列函数的周期,最大值和最小值:
解:设则
于是
于是所以
取则
由可知,所求周期为最大值为,最小值为.
例题解析
例题解析
例题解析
课堂小结
1.化简、求值;
2.恒等式证明;
3.恒等变换综合应用;
4. 三角函数的实际应用
感谢您的观看
厚久
解:原式=
(2sin2g-2sin号cos9(sin号+cos)
2sim(sincos(sn+cos兑
2x2sin2 a
2八sin2
sin F(sin2
-sin -cos a
sin
.-π0.
.sin5<0,
-sin -cos a
原式=
coS a.
证:(1)左边=1+2c0s2a-(2c0s2a-1)=2=右边
(2)左边=
2sin xcos x
2sin xcos x
s -2sin2)(2sin cos 3+2sin23)
4sin2*
sin2)
sin x
COS
2
1+cos x
右边
sin
2sin cos
sin x
解:设3sinx+4cosx=Asin(x+p),则
3sin x 4cos x Asin xcos Acos xsin
于是Ac0Sp=3,Asin=4,
于是A2c0s2p+A2sin2p=25,所以A2=25.
取A=5,则cosp=,sinp=专
由y=5sn(x+p)可知,所求周期为2π,最大值为5,最小值为-5.
5.5 三角恒等变换
必修一第五章
5.5.2 简单的三角恒等变换
知识梳理
知识梳理
知识梳理
知识梳理
例题解析
例题解析
例题解析
例2.化简:(0).
解:原式
∵0,∴
∴
∴原式
例题解析
B
例题解析
例题解析
例题解析
例题解析
例题解析
例6.(1)求证:;
(2)
证:(1)左边右边.
(2)左边
右边.
例题解析
例题解析
例题解析
例8.求下列函数的周期,最大值和最小值:
解:设则
于是
于是所以
取则
由可知,所求周期为最大值为,最小值为.
例题解析
例题解析
例题解析
课堂小结
1.化简、求值;
2.恒等式证明;
3.恒等变换综合应用;
4. 三角函数的实际应用
感谢您的观看
厚久
解:原式=
(2sin2g-2sin号cos9(sin号+cos)
2sim(sincos(sn+cos兑
2x2sin2 a
2八sin2
sin F(sin2
-sin -cos a
sin
.-π
.sin5<0,
-sin -cos a
原式=
coS a.
证:(1)左边=1+2c0s2a-(2c0s2a-1)=2=右边
(2)左边=
2sin xcos x
2sin xcos x
s -2sin2)(2sin cos 3+2sin23)
4sin2*
sin2)
sin x
COS
2
1+cos x
右边
sin
2sin cos
sin x
解:设3sinx+4cosx=Asin(x+p),则
3sin x 4cos x Asin xcos Acos xsin
于是Ac0Sp=3,Asin=4,
于是A2c0s2p+A2sin2p=25,所以A2=25.
取A=5,则cosp=,sinp=专
由y=5sn(x+p)可知,所求周期为2π,最大值为5,最小值为-5.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
