(2022秋季新教材)第六单元第3课时 三角形的面积(1)(课件)五年级数学上册 最新人教版(共39张PPT)
文档属性
| 名称 | (2022秋季新教材)第六单元第3课时 三角形的面积(1)(课件)五年级数学上册 最新人教版(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 14:22:25 | ||
图片预览



文档简介
(共39张PPT)
多边形的面积
6
人教版五年级数学上册
第3课时 三角形的面积(1)
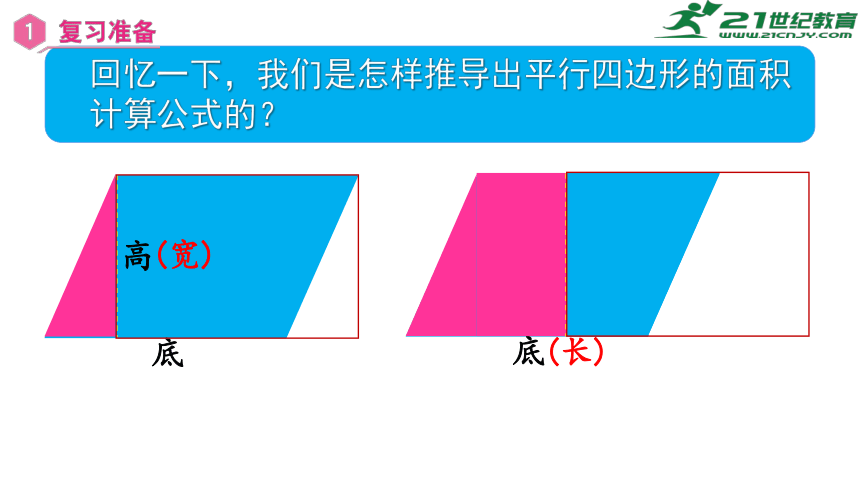
高
底
(宽)
高
底
(长)
(宽)
回忆一下,我们是怎样推导出平行四边形的面积
计算公式的?
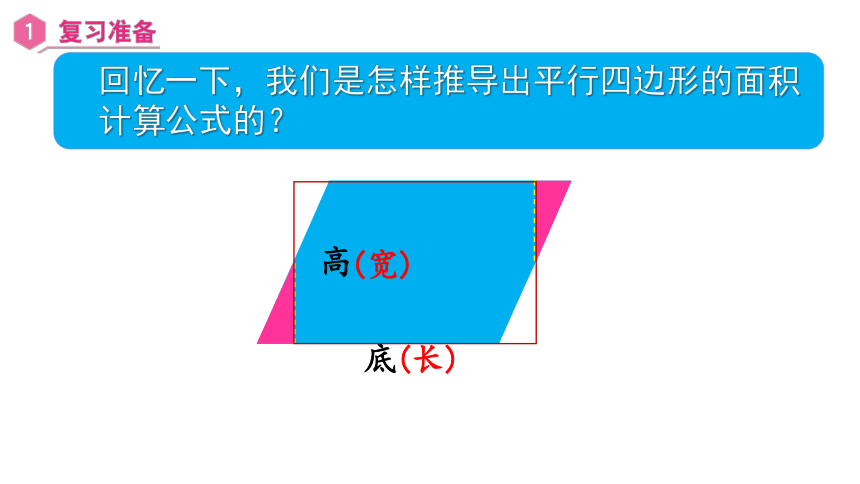
底
(长)
高
(宽)
回忆一下,我们是怎样推导出平行四边形的面积
计算公式的?
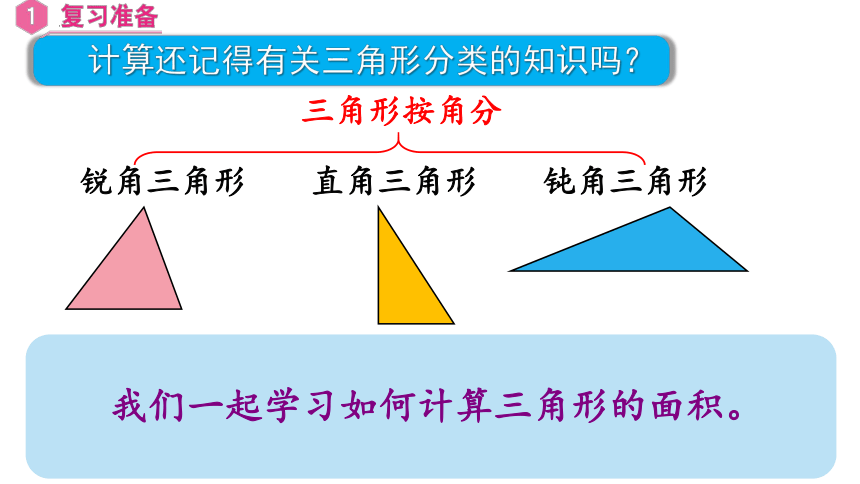
三角形按角分
锐角三角形
直角三角形
钝角三角形
计算还记得有关三角形分类的知识吗?
我们一起学习如何计算三角形的面积。
三角形的面积
红领巾的形状是三角形,怎样计算它的面积?
用两个一样的直角三角形可以拼出……
能不能把三角形也转化成学过的……
用两个同样的三角形可以拼出一个……
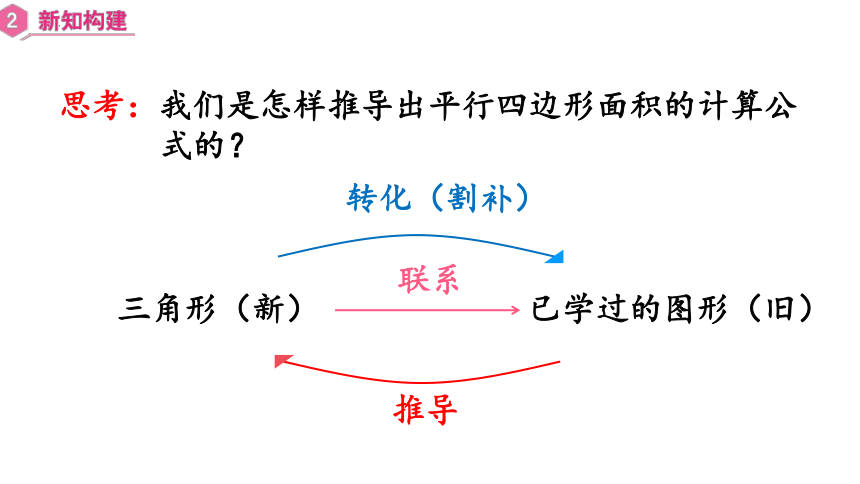
平行四边形(新) 长方形(旧)
转化(割补)
推导
联系
三角形(新)
已学过的图形(旧)
思考:我们是怎样推导出平行四边形面积的计算公
式的?
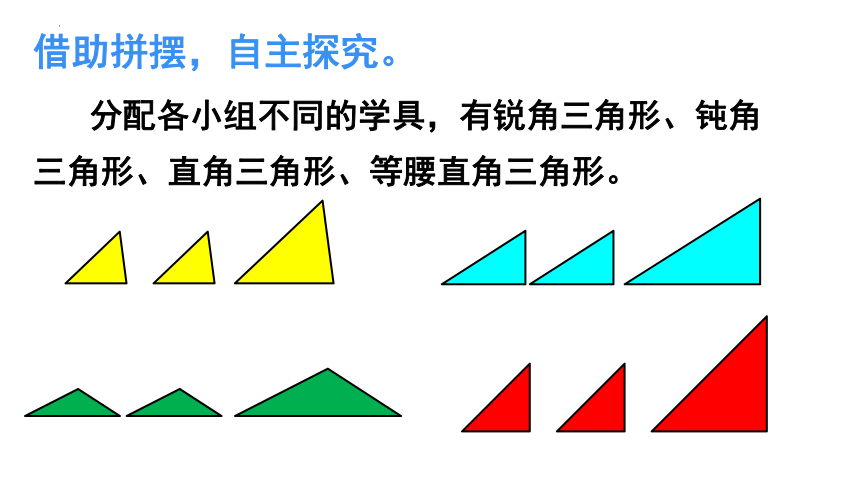
借助拼摆,自主探究。
分配各小组不同的学具,有锐角三角形、钝角三角形、直角三角形、等腰直角三角形。
3.拼出的图形与原来的三角形有什么联系?
想一想
1.你选择两个怎样的三角形拼图?能拼出什么图形?
2.拼出的图形的面积你会算吗?
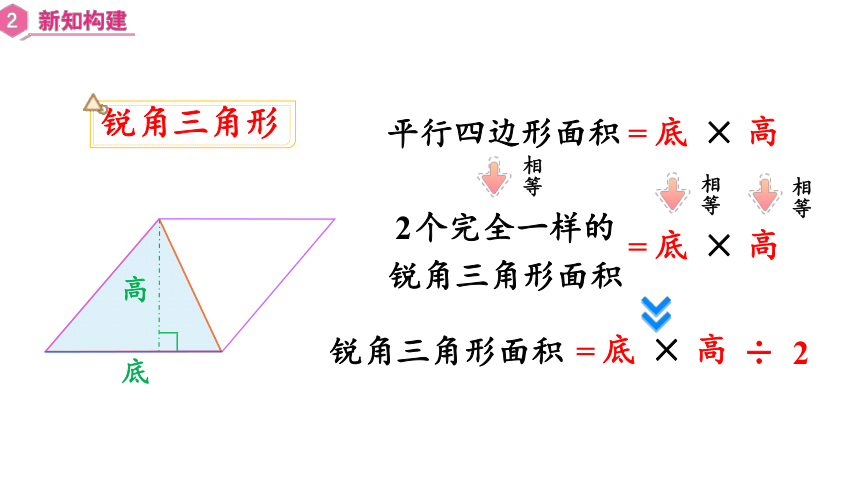
锐角三角形
底
高
平行四边形面积
底
高
×
=
相等
相等
相等
2个完全一样的
锐角三角形面积
底
高
×
=
锐角三角形面积
底
高
×
=
÷
2
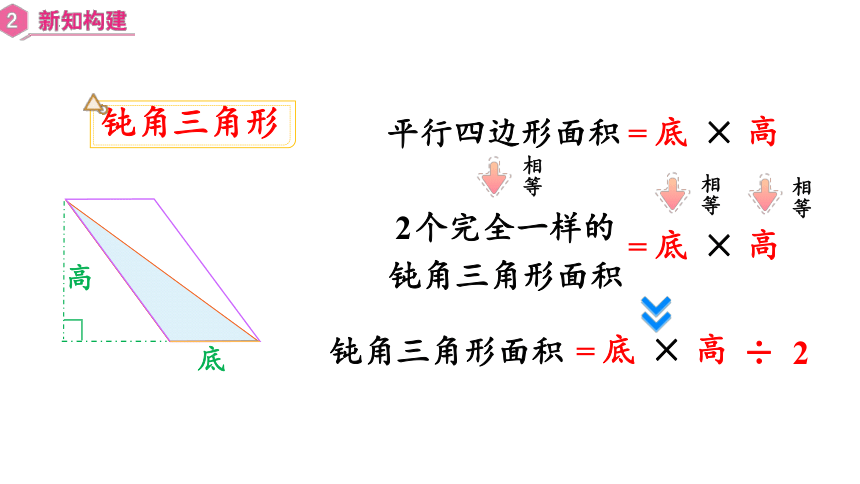
钝角三角形
底
高
平行四边形面积
底
高
×
=
相等
相等
相等
2个完全一样的
钝角三角形面积
底
高
×
=
钝角三角形面积
底
高
×
=
÷
2
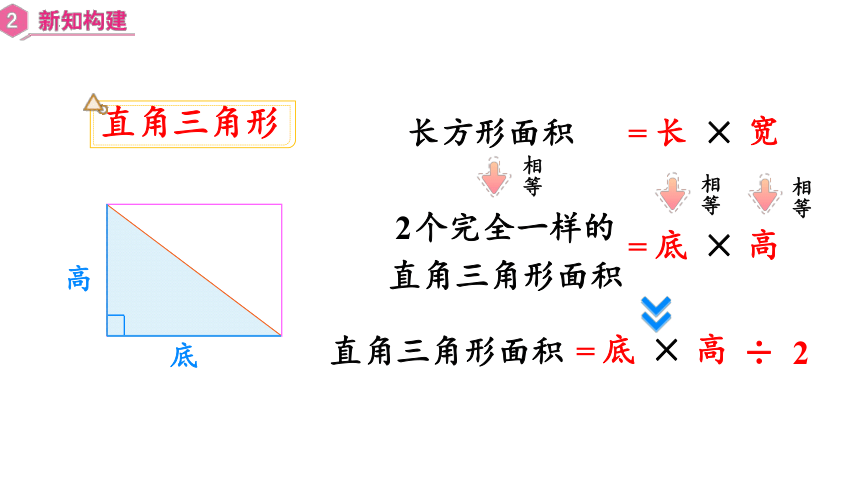
直角三角形
底
高
长方形面积
长
宽
×
=
相等
相等
相等
2个完全一样的
直角三角形面积
底
高
×
=
直角三角形面积
底
高
×
=
÷
2
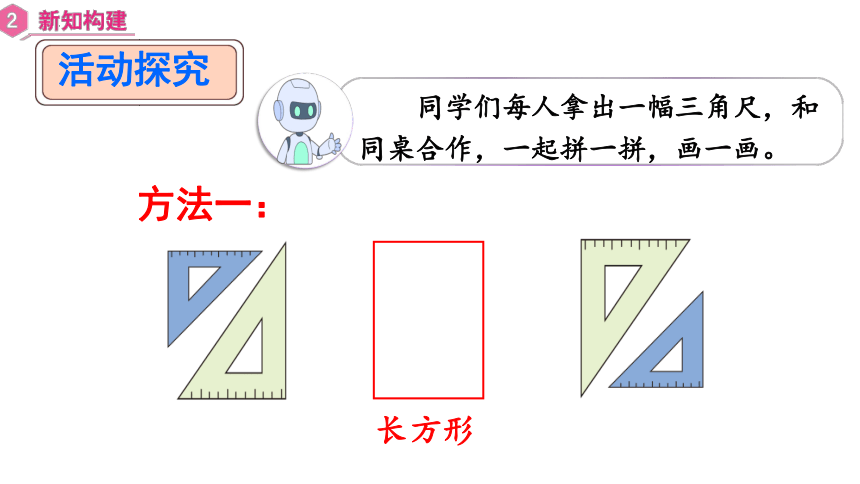
同学们每人拿出一幅三角尺,和同桌合作,一起拼一拼,画一画。
活动探究
方法一:
长方形
同学们每人拿出一幅三角尺,和同桌合作,一起拼一拼,画一画。
活动探究
方法二:
正方形
剪拼法
底
高
平行四边形的面积 = 底 × 高
三角形的面积 = 底 ×(高÷2)
三角形的面积 = 底 × 高÷2
探究三角形面积计算公式的其他方法
底
高
剪拼法
长方形的面积 = 长 × 宽
三角形的面积 = 底 ×(高÷2)
三角形的面积 = 底 × 高÷2
探究三角形面积计算公式的其他方法
折叠法
长方形的面积 = 长 × 宽
三角形的面积的一半 =(底÷2)×(高÷2)
三角形的面积 = 底 × 高÷2
探究三角形面积计算公式的其他方法
只要是两个完全一样的三角形,我们就能把
它们拼成一个平行四边形或长方形、正方形。
每个三角形的面积 = 平行四边形面积的一半。
高
底
高
底
高
底
两个完全一样的三角形都可以拼成一个平行四边形。
这个平行四边形的底和高分别等于三角形的底和高。
观察拼成的平行四边形和原来的三角形,你发现了什么?
高
底
高
底
高
底
三角形的面积 = 平行四边面积的一半
= 底×高÷2
三角形的面积=底×高÷2
平行四边形的底相当于三角形的( ),
平行四边形的高相当于三角形的( )。
底
高
观察拼成的平行四边形和原来的三角形,你发现了什么?
如果用S表示三角形的面积,用 a和h分别表示三角形的底和高,那么三角形的面积计算公式可以写成:
S = ah÷2
易错点:用三角形的面积计算公式求三角形的面积时,底与高要对应,底与高的乘积要除以2。
教材第90页例2
红领巾的底是 120 cm,高 39.8 cm,它的面积是多少平方厘米?
S = ah÷2
= 120×39.8÷2
= 2388(cm2)
答:它的面积是 1650 cm2。
39.8cm
120 cm
利用公式求面积:先写字母公式,再代入数值计算,最后加上单位。
2
归纳总结:
三角形的面积=底×高÷2,
用字母表示三角形的面积计算公式为S=ah÷2。
注意:求任意三角形(锐角三角形、直角三角形、钝角三角形)的面积,该面积计算公式都适用,但计算三角形的面积时,底和高必须要对应。
1. 填一填。
(1)两个( )的三角形可以拼成一个平行四边形,每个三角形的面积是拼成的平行四边形面积的( ),所以三角形的面积=平行四边形的面积÷( ),用字母表示是( )。
(2)如果上面平行四边形的面积是6.8 cm ,则其中一个三角形的面积是( )cm 。
(3)如果上面其中一个三角形的底是3.5 dm,高是2 dm,则它的面积是( )dm 。
完全一样
一半
2
S=ah÷2
3.4
3.5
2. 判断(对的打√,错的打×)。
(1)三角形的底越长,它的面积越大。 ( )
(2)两个面积相等的三角形,一定可以拼成一个平行四边形。 ( )
(3)面积相等的三角形,周长可能相等。( )
(4)等底等高的三角形面积相等。 ( )
(5)平行四边形的面积是三角形面积的2倍。 ( )(6)三角形的底和高扩大到原来的2倍,则面积也扩大到原来的2倍。 ( )
×
×
√
√
还与高有关系。
形状不一定相同。
×
×
3. 选一选。
(1)两个完全一样的锐角三角形,可以拼成一个( )。
A.长方形 B.正方形 C.梯形 D.平行四边形
(2)要计算三角形的面积,必须要知道它的( )。
A.底和高 B.底和面积 C.高和面积
(3)一个三角形的面积是 4.8,与它等底等高的平行四边形的面积是( )。
A. 4.8 B. 9.6 C. 1.6 D.无法确定
D
A
B
教材第90页“做一做”
1. 下面平行四边形的面积是 12 cm ,求涂色的三角形的面积。
12 ÷ 2 = 6(cm2)
涂色的三角形的面积=平行四边形面积的一半。
答:涂色的三角形的面积是 6 cm2。
做一做
三角尺是直角三角形,它的两条直角边就是三角形的底和高。
2.一种三角尺的形状如下图,它的面积是多少?
S = ah÷2
= 12.5×7.2÷2
= 45(cm2)
答:它的面积是45 cm2。
12.5 cm
7.2 cm
底
高
教材第90页“做一做”
做一做
直接用S=ah÷2进行计算。结果注意加上单位。
3. 如图,一种零件有一面是三角形。三角形的底是5.6 cm,高是4 cm,这个三角形的面积是多少平方厘米?
S=ah÷2
=5.6×4÷2
=11.2(cm2)
答:这个三角形的面积是11.2 cm2。
4 cm
5.6 cm
教材第90页“做一做”
做一做
教材第91页第1题
4. 你认识下面这些道路交通警示标志吗?一块标志牌的面积大约是多少平方分米?
7.8 dm
9 dm
答:一块标志牌的面积大约是35.1平方分米。
注意:求三角形的面积,除以2不要忘了!
注意危险
慢行
注意行人
向右
急转弯
S=ah÷2
=7.8×9÷2
=35.1(平方分米)
5.指出下面每个三角形的底和高,并分别计算出它们的面积。
3 cm
4 cm
0.9 dm
4 dm
2.5 dm
2.8 dm
底
高
底
高
底
高
教材第91页第2题
5.指出下面每个三角形的底和高,并分别计算出它们的面积。
3 cm
4 cm
0.9 dm
4 dm
2.5 dm
2.8 dm
S=ah÷2
=3×4÷2
=6(cm2)
S=ah÷2
=4×0.9÷2
=1.8(cm2)
S=ah÷2
=2.5×2.8÷2
=3.5(cm2)
教材第91页第2题
在计算三角形面积时,能不能用4×8或者5×10?
易错点
10 cm
8 cm
4 cm
5 cm
计算三角形面积和计算平行四边形的面积一样,底和高应该是对应的,不能交错相乘。
6. 要在公路中间的一块三角形空地(见下图)上种草坪。1 m 草坪的价格是12元。种这片草坪需要多少钱?
16×9.5÷2=76(m )
16m
9.5 m
76×12= 912(元)
答:种这片草坪需要912元。
1.求出草坪的面积。
教材第91页第4题
2.按“总价 =单价×面积” 求出总价。
7.如图,平行四边形的面积是80 cm2,求阴影部分的面积。
80÷8=10(cm)
(10-8)×8÷2=8(cm2)
答:阴影部分的面积是8 cm2。
8.(易错题)如图,平行四边形的面积是50 cm2,求阴影部分的面积。
50÷5=10(cm)
(10-7)×5÷2=7.5(cm2)
答:阴影部分的面积为7.5 cm2。
5 cm
10 cm
4 cm
由平行线之间的距离处处相等,可知长方形的 、三角形的 和平行四边形的 。
长方形的面积已知,就可以求出长。
9. 下图中的长方形的面积是40平方厘米,则三角形的面积是( )平方厘米,平行四边形的面积是( )平方厘米。
高
高
长
相等
9. 下图中的长方形的面积是40平方厘米,则三角形的面积是( )平方厘米,平行四边形的面积是( )平方厘米。
长:40÷5=8(cm)
三角形面积:10×8÷2=40(cm )
平行四边形面积:4×8=32(cm )
40
32
5 cm
10 cm
4 cm
大约在两千年前,我国数学名著《九章算术》中的“方田章”就论 述了平面图形面积的算法。书中说:“方田术曰,广从步数相乘得积步。”其中“方田”是指长方形田地,“广”和“从”是指长和宽,也就是说:长方形面积 = 长×宽。还说:“圭田术曰,半广以乘正从。”就是说: 三角形面积 =底×高÷2。
你知道吗?
求三角形面积
求平行四边形面积
转化
1. 两个完全相同的三角形可以拼成一个平行四边形。
2. 三角形的面积=底×高÷2,用字母表示为S=ah÷2。
3. 在利用S=ah÷2求面积时,同样要用相对应的底和高才能得出正确的结果。
这节课你有什么收获?
多边形的面积
6
人教版五年级数学上册
第3课时 三角形的面积(1)
高
底
(宽)
高
底
(长)
(宽)
回忆一下,我们是怎样推导出平行四边形的面积
计算公式的?
底
(长)
高
(宽)
回忆一下,我们是怎样推导出平行四边形的面积
计算公式的?
三角形按角分
锐角三角形
直角三角形
钝角三角形
计算还记得有关三角形分类的知识吗?
我们一起学习如何计算三角形的面积。
三角形的面积
红领巾的形状是三角形,怎样计算它的面积?
用两个一样的直角三角形可以拼出……
能不能把三角形也转化成学过的……
用两个同样的三角形可以拼出一个……
平行四边形(新) 长方形(旧)
转化(割补)
推导
联系
三角形(新)
已学过的图形(旧)
思考:我们是怎样推导出平行四边形面积的计算公
式的?
借助拼摆,自主探究。
分配各小组不同的学具,有锐角三角形、钝角三角形、直角三角形、等腰直角三角形。
3.拼出的图形与原来的三角形有什么联系?
想一想
1.你选择两个怎样的三角形拼图?能拼出什么图形?
2.拼出的图形的面积你会算吗?
锐角三角形
底
高
平行四边形面积
底
高
×
=
相等
相等
相等
2个完全一样的
锐角三角形面积
底
高
×
=
锐角三角形面积
底
高
×
=
÷
2
钝角三角形
底
高
平行四边形面积
底
高
×
=
相等
相等
相等
2个完全一样的
钝角三角形面积
底
高
×
=
钝角三角形面积
底
高
×
=
÷
2
直角三角形
底
高
长方形面积
长
宽
×
=
相等
相等
相等
2个完全一样的
直角三角形面积
底
高
×
=
直角三角形面积
底
高
×
=
÷
2
同学们每人拿出一幅三角尺,和同桌合作,一起拼一拼,画一画。
活动探究
方法一:
长方形
同学们每人拿出一幅三角尺,和同桌合作,一起拼一拼,画一画。
活动探究
方法二:
正方形
剪拼法
底
高
平行四边形的面积 = 底 × 高
三角形的面积 = 底 ×(高÷2)
三角形的面积 = 底 × 高÷2
探究三角形面积计算公式的其他方法
底
高
剪拼法
长方形的面积 = 长 × 宽
三角形的面积 = 底 ×(高÷2)
三角形的面积 = 底 × 高÷2
探究三角形面积计算公式的其他方法
折叠法
长方形的面积 = 长 × 宽
三角形的面积的一半 =(底÷2)×(高÷2)
三角形的面积 = 底 × 高÷2
探究三角形面积计算公式的其他方法
只要是两个完全一样的三角形,我们就能把
它们拼成一个平行四边形或长方形、正方形。
每个三角形的面积 = 平行四边形面积的一半。
高
底
高
底
高
底
两个完全一样的三角形都可以拼成一个平行四边形。
这个平行四边形的底和高分别等于三角形的底和高。
观察拼成的平行四边形和原来的三角形,你发现了什么?
高
底
高
底
高
底
三角形的面积 = 平行四边面积的一半
= 底×高÷2
三角形的面积=底×高÷2
平行四边形的底相当于三角形的( ),
平行四边形的高相当于三角形的( )。
底
高
观察拼成的平行四边形和原来的三角形,你发现了什么?
如果用S表示三角形的面积,用 a和h分别表示三角形的底和高,那么三角形的面积计算公式可以写成:
S = ah÷2
易错点:用三角形的面积计算公式求三角形的面积时,底与高要对应,底与高的乘积要除以2。
教材第90页例2
红领巾的底是 120 cm,高 39.8 cm,它的面积是多少平方厘米?
S = ah÷2
= 120×39.8÷2
= 2388(cm2)
答:它的面积是 1650 cm2。
39.8cm
120 cm
利用公式求面积:先写字母公式,再代入数值计算,最后加上单位。
2
归纳总结:
三角形的面积=底×高÷2,
用字母表示三角形的面积计算公式为S=ah÷2。
注意:求任意三角形(锐角三角形、直角三角形、钝角三角形)的面积,该面积计算公式都适用,但计算三角形的面积时,底和高必须要对应。
1. 填一填。
(1)两个( )的三角形可以拼成一个平行四边形,每个三角形的面积是拼成的平行四边形面积的( ),所以三角形的面积=平行四边形的面积÷( ),用字母表示是( )。
(2)如果上面平行四边形的面积是6.8 cm ,则其中一个三角形的面积是( )cm 。
(3)如果上面其中一个三角形的底是3.5 dm,高是2 dm,则它的面积是( )dm 。
完全一样
一半
2
S=ah÷2
3.4
3.5
2. 判断(对的打√,错的打×)。
(1)三角形的底越长,它的面积越大。 ( )
(2)两个面积相等的三角形,一定可以拼成一个平行四边形。 ( )
(3)面积相等的三角形,周长可能相等。( )
(4)等底等高的三角形面积相等。 ( )
(5)平行四边形的面积是三角形面积的2倍。 ( )(6)三角形的底和高扩大到原来的2倍,则面积也扩大到原来的2倍。 ( )
×
×
√
√
还与高有关系。
形状不一定相同。
×
×
3. 选一选。
(1)两个完全一样的锐角三角形,可以拼成一个( )。
A.长方形 B.正方形 C.梯形 D.平行四边形
(2)要计算三角形的面积,必须要知道它的( )。
A.底和高 B.底和面积 C.高和面积
(3)一个三角形的面积是 4.8,与它等底等高的平行四边形的面积是( )。
A. 4.8 B. 9.6 C. 1.6 D.无法确定
D
A
B
教材第90页“做一做”
1. 下面平行四边形的面积是 12 cm ,求涂色的三角形的面积。
12 ÷ 2 = 6(cm2)
涂色的三角形的面积=平行四边形面积的一半。
答:涂色的三角形的面积是 6 cm2。
做一做
三角尺是直角三角形,它的两条直角边就是三角形的底和高。
2.一种三角尺的形状如下图,它的面积是多少?
S = ah÷2
= 12.5×7.2÷2
= 45(cm2)
答:它的面积是45 cm2。
12.5 cm
7.2 cm
底
高
教材第90页“做一做”
做一做
直接用S=ah÷2进行计算。结果注意加上单位。
3. 如图,一种零件有一面是三角形。三角形的底是5.6 cm,高是4 cm,这个三角形的面积是多少平方厘米?
S=ah÷2
=5.6×4÷2
=11.2(cm2)
答:这个三角形的面积是11.2 cm2。
4 cm
5.6 cm
教材第90页“做一做”
做一做
教材第91页第1题
4. 你认识下面这些道路交通警示标志吗?一块标志牌的面积大约是多少平方分米?
7.8 dm
9 dm
答:一块标志牌的面积大约是35.1平方分米。
注意:求三角形的面积,除以2不要忘了!
注意危险
慢行
注意行人
向右
急转弯
S=ah÷2
=7.8×9÷2
=35.1(平方分米)
5.指出下面每个三角形的底和高,并分别计算出它们的面积。
3 cm
4 cm
0.9 dm
4 dm
2.5 dm
2.8 dm
底
高
底
高
底
高
教材第91页第2题
5.指出下面每个三角形的底和高,并分别计算出它们的面积。
3 cm
4 cm
0.9 dm
4 dm
2.5 dm
2.8 dm
S=ah÷2
=3×4÷2
=6(cm2)
S=ah÷2
=4×0.9÷2
=1.8(cm2)
S=ah÷2
=2.5×2.8÷2
=3.5(cm2)
教材第91页第2题
在计算三角形面积时,能不能用4×8或者5×10?
易错点
10 cm
8 cm
4 cm
5 cm
计算三角形面积和计算平行四边形的面积一样,底和高应该是对应的,不能交错相乘。
6. 要在公路中间的一块三角形空地(见下图)上种草坪。1 m 草坪的价格是12元。种这片草坪需要多少钱?
16×9.5÷2=76(m )
16m
9.5 m
76×12= 912(元)
答:种这片草坪需要912元。
1.求出草坪的面积。
教材第91页第4题
2.按“总价 =单价×面积” 求出总价。
7.如图,平行四边形的面积是80 cm2,求阴影部分的面积。
80÷8=10(cm)
(10-8)×8÷2=8(cm2)
答:阴影部分的面积是8 cm2。
8.(易错题)如图,平行四边形的面积是50 cm2,求阴影部分的面积。
50÷5=10(cm)
(10-7)×5÷2=7.5(cm2)
答:阴影部分的面积为7.5 cm2。
5 cm
10 cm
4 cm
由平行线之间的距离处处相等,可知长方形的 、三角形的 和平行四边形的 。
长方形的面积已知,就可以求出长。
9. 下图中的长方形的面积是40平方厘米,则三角形的面积是( )平方厘米,平行四边形的面积是( )平方厘米。
高
高
长
相等
9. 下图中的长方形的面积是40平方厘米,则三角形的面积是( )平方厘米,平行四边形的面积是( )平方厘米。
长:40÷5=8(cm)
三角形面积:10×8÷2=40(cm )
平行四边形面积:4×8=32(cm )
40
32
5 cm
10 cm
4 cm
大约在两千年前,我国数学名著《九章算术》中的“方田章”就论 述了平面图形面积的算法。书中说:“方田术曰,广从步数相乘得积步。”其中“方田”是指长方形田地,“广”和“从”是指长和宽,也就是说:长方形面积 = 长×宽。还说:“圭田术曰,半广以乘正从。”就是说: 三角形面积 =底×高÷2。
你知道吗?
求三角形面积
求平行四边形面积
转化
1. 两个完全相同的三角形可以拼成一个平行四边形。
2. 三角形的面积=底×高÷2,用字母表示为S=ah÷2。
3. 在利用S=ah÷2求面积时,同样要用相对应的底和高才能得出正确的结果。
这节课你有什么收获?
