(2022秋季新教材)第六单元第1课时 平行四边形的面积(1)(课件)五年级数学上册 最新人教版(共35张PPT)
文档属性
| 名称 | (2022秋季新教材)第六单元第1课时 平行四边形的面积(1)(课件)五年级数学上册 最新人教版(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 00:00:00 | ||
图片预览


文档简介
(共35张PPT)
多边形的面积
6
人教版五年级数学上册
第1课时 平行四边形的面积(1)
你发现了哪些图形?你会计算它们的面积吗?
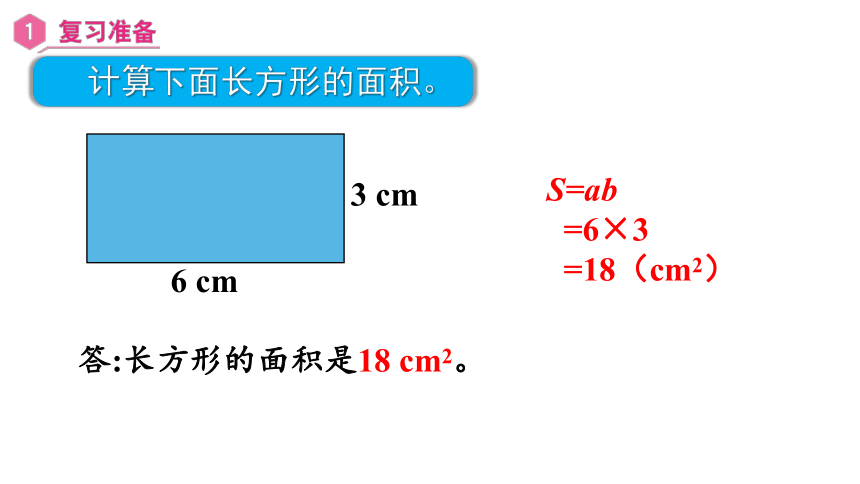
S=ab
=6×3
=18(cm2)
答:长方形的面积是18 cm2。
6 cm
3 cm
计算下面长方形的面积。
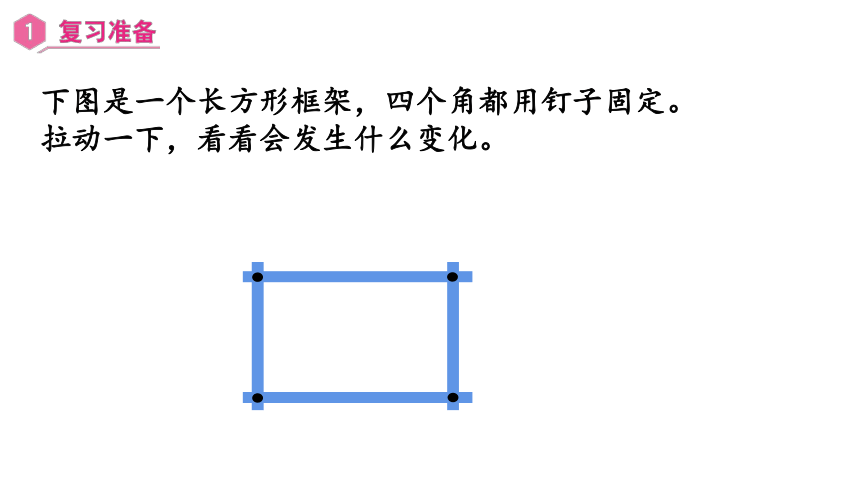
下图是一个长方形框架,四个角都用钉子固定。
拉动一下,看看会发生什么变化。
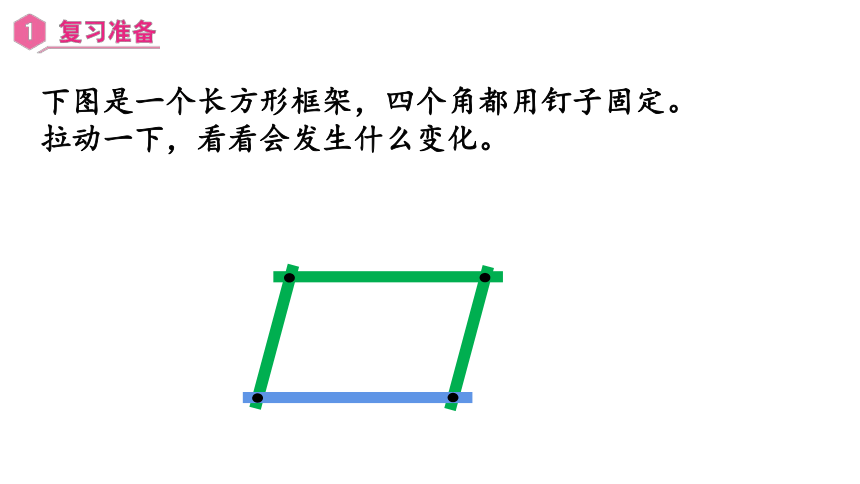
下图是一个长方形框架,四个角都用钉子固定。
拉动一下,看看会发生什么变化。
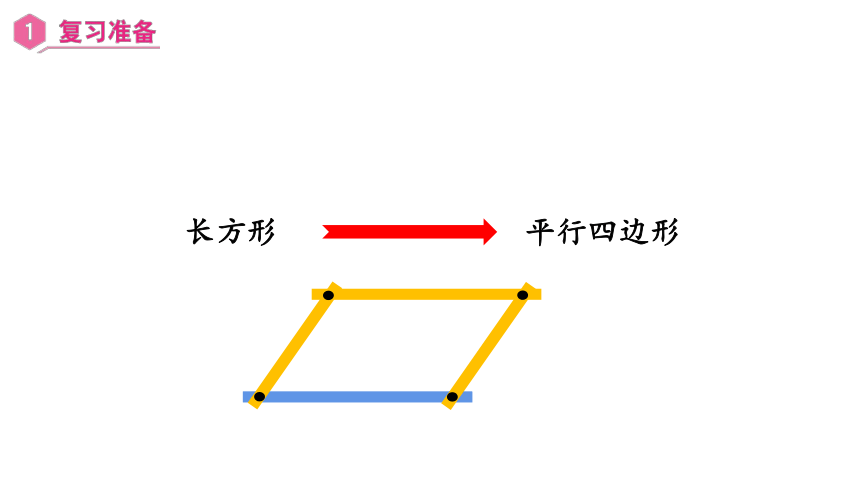
长方形
平行四边形
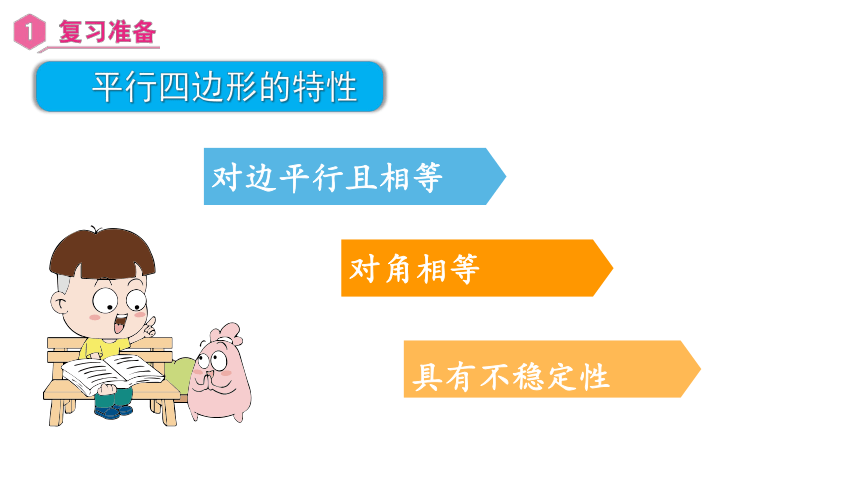
平行四边形的特性
具有不稳定性
对角相等
对边平行且相等
教材第87页
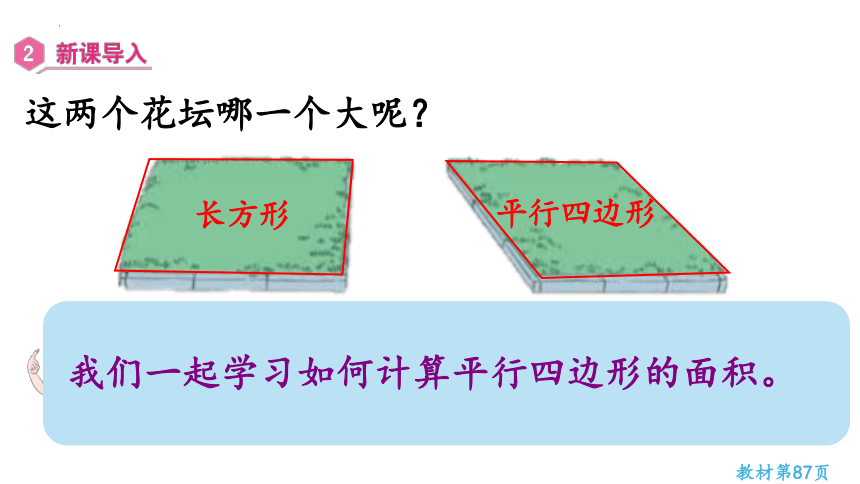
要判断花坛哪一个大,要知道它们的面积。但只会算长方形的面积,长方形的面积=长×宽
长方形
平行四边形
这两个花坛哪一个大呢?
我们一起学习如何计算平行四边形的面积。
重叠比较
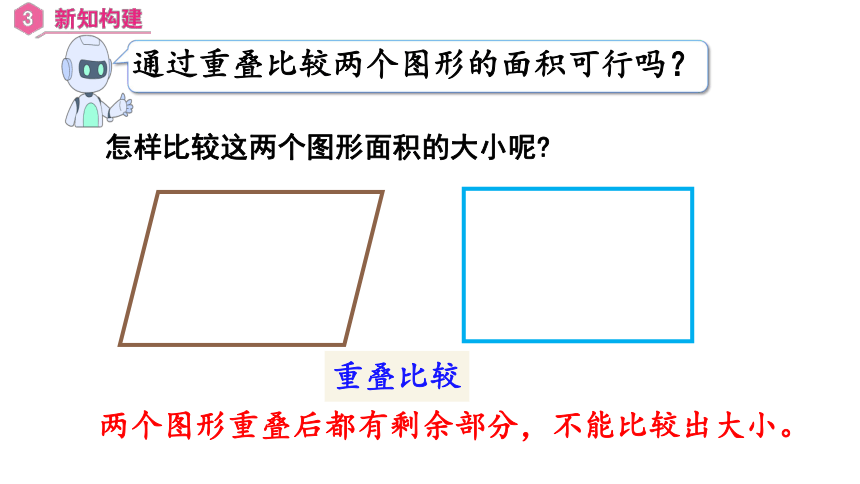
怎样比较这两个图形面积的大小呢
通过重叠比较两个图形的面积可行吗?
两个图形重叠后都有剩余部分,不能比较出大小。
5
+0.5
=24(m )
=24(m )
6
×4
×4
×2
×4
1m
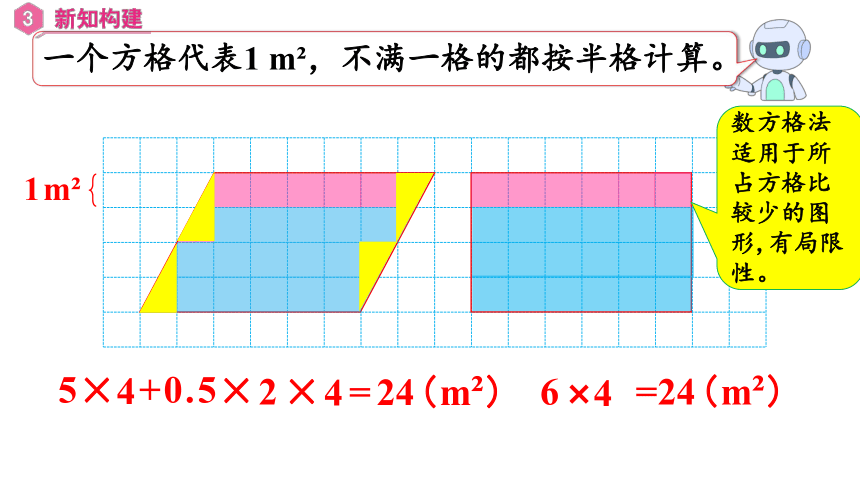
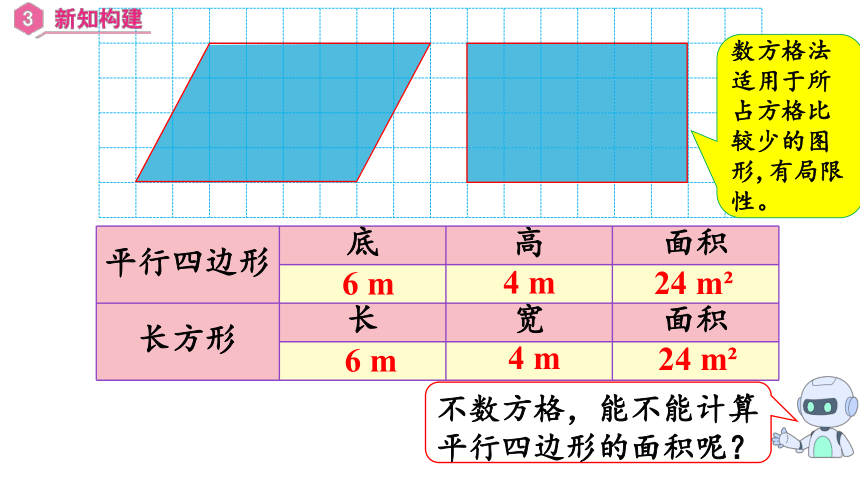
用数方格的方式试一试。
一个方格代表1 m ,不满一格的都按半格计算。
数方格法适用于所占方格比较少的图形,有局限性。
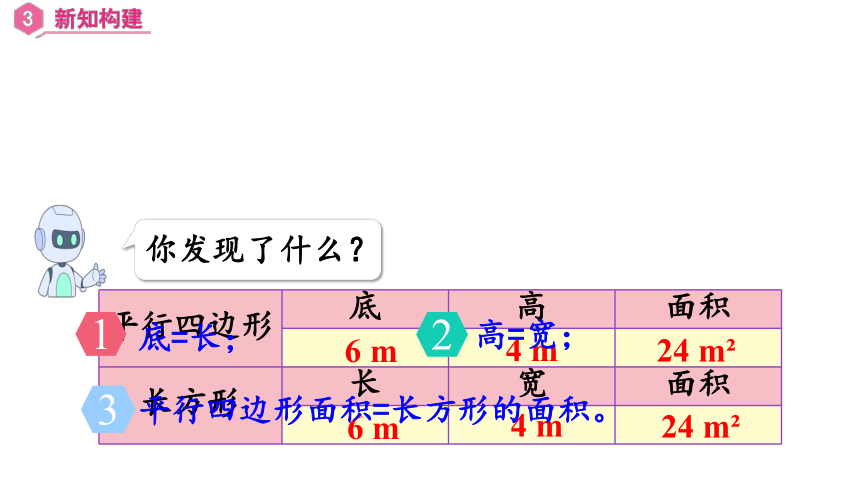
平行四边形 底 高 面积
长方形 长 宽 面积
6 m
6 m
4 m
4 m
24 m
24 m
你发现了什么?
底=长;
1
高=宽;
2
平行四边形面积=长方形的面积。
3
平行四边形 底 高 面积
长方形 长 宽 面积
6 m
6 m
4 m
4 m
24 m
24 m
不数方格,能不能计算平行四边形的面积呢?
数方格法适用于所占方格比较少的图形,有局限性。
平行四边形的面积
先沿高剪开,把三角形向右平移,再拼成……
可以把平行四边形变成一个长方形。
转化成长方形就能计算面积了。
教材第86页
高
底
平行四边形的面积
×
底
高
长方形的面积 =
×
长
宽
(长)
(宽)
“割补”法
二
拼
一
剪
=
高
底
(长)
(宽)
“割补”法
二
拼
一
剪
平行四边形的面积
×
底
高
长方形的面积 =
×
长
宽
=
底
(长)
高
(宽)
“割补”法
二
拼
一
剪
平行四边形的面积
×
底
高
长方形的面积 =
×
长
宽
=
观察原来的平行四边形和转化后的长方形,你发现它们之间有哪些等量关系?
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
平行四边形的底和长方形的长相等;平行四边形的高和长方形的宽相等;这两个图形的面积相等。
如果用S表示平行四边形的面积,用 a 表示平行四边形的底,用h表示平行四边形的高,平行四边形的面积计算公式可以写成:
S = ah
教材第86页例1
6m
4m
S=ah
=6×4
=24(m2)
答:平行四边形花坛的面积是24m2。
平行四边形花坛的底是6m,高是4m,它的面积是多少?
写出字母公式
将数据代入字母公式
计算结果,加上单位
1
1.运用平行四边形的面积计算公式解决实际问题,应找准底和对应的高。
2.注意底和高的单位的一致,最后结果带上单位名称。
3.运用公式解决问题时,通常先把用到的字母公式写出来,然后代入数据进行计算。
推导平行四边形的面积公式。
如图,把一个平行四边形用割补法转化成一个 ( ),这个( )的面积与原来平行四边形的面积( );
1.填空。
长方形
长方形
相等
长方形的长就是平行四边形的( ),长方形的宽就是平行四边形的( )。因为长方形的面积=( ),所以平行四边形的面积=( ),如果用字母S表示平行四边形的面积,用字母a表示平行四边形的底,用字母h表示平行四边形的高,那么平行四边形的面积计算公式是( )。
底
高
长×宽
底×高
S=ah
2. 计算平行四边形的面积,把正确的算式圈出来。
注意:在计算平行四边形面积时底和高相互对应!
6×5
B. 10×6
C. 10×5
5×4.5
4×4.5
C. 5×4
5 cm
10 cm
6 cm
4 cm
5 cm
4.5 cm
3. 选一选。
(1)如图,这个平行四边形的面积是( )。
150 cm B. 80 cm C. 120 cm D. 180 cm
C
(2)(易错题)一个平行四边形的底不变,高扩大到原来的2倍,面积( )。
A.不变
B.扩大到原来的2倍
C.扩大到原来的4倍
D.扩大到原来的8倍
B
3. 选一选。
(3)一个平行四边形的底扩大到原来的2倍,高缩小到原来的一半,面积( )。
A.扩大到原来的4倍
B.不变
C.缩小到原来的一半
B
3. 选一选。
3. 选一选。
(4)一块平行四边形菜地,底是450米,高是200米,这块菜地有( )公顷。
A. 9 B. 90 C. 900 D. 90000
(5)一个平行四边形的底扩大到原来的2倍,高不变,面积就扩大到原来的( )倍;如果底和高都扩大到原来的2倍,那么面积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
A
A
B
4. 一个停车位是平行四边形,它的底是 5 米,它的高是 2.5 米,它的面积是多少?
S = ah
= 5×2.5
= 12.5(m2)
答:这个停车位的面积是 12.5 m2。
注意书写格式,结果单位不要忘记。
教材第87页第1题
5. 计算下面平行四边形的面积。
S = ah
= 4×3
= 12(cm2)
S = ah
= 5.2×3.6
= 18.72(cm2)
教材第87页第2题
4 cm
3 cm
5.2 cm
3.6 cm
2 cm
2.4 cm
1.6 cm
3 cm
注意底和高的对应性。
S=ah
5. 计算下面平行四边形的面积。
教材第87页第2题
S = ah
= 2×2.4
= 4.8(cm )
S = ah
= 3×1.6
= 4.8(cm )
方法一:
方法二:
2 cm
2.4 cm
3 cm
S=ah
1.6 cm
6.下表给出的是平行四边形的底和高,计算出每个平行四边形的面积,填在空格里。
底/cm 38 70 6.2 21.5 18 0.9
高/cm 21 15 26 9.8 5.2 0.4
面积/cm2
798
1050
161.2
210.7
93.6
0.36
教材第87页第3题
7.你能想办法求出右面两个平行四边形的面积吗?
提示:自己用刻度尺量出每个平行四边形的底和高,
利用公式求出它们的面积。
教材第87页第4题
8. 有一块麦田的形状是平行四边形。它的底是250 m,高是84 m,共收小麦14.7吨。这块麦田有多少公顷?平均每公顷收小麦多少吨?
麦田面积: 250×84 = 21000(m2)
单位换算: 21000 m2 = 2.1 (公顷)
平均收麦: 14.7÷2.1 = 7(吨)
答:这块麦田有2.1公顷,平均每公顷收小麦7吨。
要求麦田有多少公顷,实际是求这块麦田的面积。
教材第87页第5题
9.在一块底是8 m,高是6 m的平行四边形地里种萝
卜。如果每平方米收萝卜7.5 kg,这块地可收萝卜
多少千克?
8×6=48(m2)
7.5×48=360(kg)
答:这块地可收萝卜360千克。
10. 一块平行四边形的地,底是10.5 m,高是6.4 m,如果用这块地种辣椒,每棵辣椒占地 0.2 m2,这块地一共可以种多少棵辣椒?
这块地的面积:10.5×6.4 = 67.2(m2)
种辣椒棵树: 67.2÷0.2 = 336(棵)
答:这块地一共可以种336棵辣椒。
要求辣椒种植棵数,先要求出这块地的总面积。然后用“总面积÷每棵辣椒的占地面积=种植棵数”即可求解。
平行四边形的面积
×
底
高
长方形的面积 =
×
长
宽
=
S=a×h=a·h=ah
平行四边形的面积=底×高,在利用S=ah求面积时,要用相对应的底和高才能得出正确的结果。
这节课你有什么收获?
多边形的面积
6
人教版五年级数学上册
第1课时 平行四边形的面积(1)
你发现了哪些图形?你会计算它们的面积吗?
S=ab
=6×3
=18(cm2)
答:长方形的面积是18 cm2。
6 cm
3 cm
计算下面长方形的面积。
下图是一个长方形框架,四个角都用钉子固定。
拉动一下,看看会发生什么变化。
下图是一个长方形框架,四个角都用钉子固定。
拉动一下,看看会发生什么变化。
长方形
平行四边形
平行四边形的特性
具有不稳定性
对角相等
对边平行且相等
教材第87页
要判断花坛哪一个大,要知道它们的面积。但只会算长方形的面积,长方形的面积=长×宽
长方形
平行四边形
这两个花坛哪一个大呢?
我们一起学习如何计算平行四边形的面积。
重叠比较
怎样比较这两个图形面积的大小呢
通过重叠比较两个图形的面积可行吗?
两个图形重叠后都有剩余部分,不能比较出大小。
5
+0.5
=24(m )
=24(m )
6
×4
×4
×2
×4
1m
用数方格的方式试一试。
一个方格代表1 m ,不满一格的都按半格计算。
数方格法适用于所占方格比较少的图形,有局限性。
平行四边形 底 高 面积
长方形 长 宽 面积
6 m
6 m
4 m
4 m
24 m
24 m
你发现了什么?
底=长;
1
高=宽;
2
平行四边形面积=长方形的面积。
3
平行四边形 底 高 面积
长方形 长 宽 面积
6 m
6 m
4 m
4 m
24 m
24 m
不数方格,能不能计算平行四边形的面积呢?
数方格法适用于所占方格比较少的图形,有局限性。
平行四边形的面积
先沿高剪开,把三角形向右平移,再拼成……
可以把平行四边形变成一个长方形。
转化成长方形就能计算面积了。
教材第86页
高
底
平行四边形的面积
×
底
高
长方形的面积 =
×
长
宽
(长)
(宽)
“割补”法
二
拼
一
剪
=
高
底
(长)
(宽)
“割补”法
二
拼
一
剪
平行四边形的面积
×
底
高
长方形的面积 =
×
长
宽
=
底
(长)
高
(宽)
“割补”法
二
拼
一
剪
平行四边形的面积
×
底
高
长方形的面积 =
×
长
宽
=
观察原来的平行四边形和转化后的长方形,你发现它们之间有哪些等量关系?
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
平行四边形的底和长方形的长相等;平行四边形的高和长方形的宽相等;这两个图形的面积相等。
如果用S表示平行四边形的面积,用 a 表示平行四边形的底,用h表示平行四边形的高,平行四边形的面积计算公式可以写成:
S = ah
教材第86页例1
6m
4m
S=ah
=6×4
=24(m2)
答:平行四边形花坛的面积是24m2。
平行四边形花坛的底是6m,高是4m,它的面积是多少?
写出字母公式
将数据代入字母公式
计算结果,加上单位
1
1.运用平行四边形的面积计算公式解决实际问题,应找准底和对应的高。
2.注意底和高的单位的一致,最后结果带上单位名称。
3.运用公式解决问题时,通常先把用到的字母公式写出来,然后代入数据进行计算。
推导平行四边形的面积公式。
如图,把一个平行四边形用割补法转化成一个 ( ),这个( )的面积与原来平行四边形的面积( );
1.填空。
长方形
长方形
相等
长方形的长就是平行四边形的( ),长方形的宽就是平行四边形的( )。因为长方形的面积=( ),所以平行四边形的面积=( ),如果用字母S表示平行四边形的面积,用字母a表示平行四边形的底,用字母h表示平行四边形的高,那么平行四边形的面积计算公式是( )。
底
高
长×宽
底×高
S=ah
2. 计算平行四边形的面积,把正确的算式圈出来。
注意:在计算平行四边形面积时底和高相互对应!
6×5
B. 10×6
C. 10×5
5×4.5
4×4.5
C. 5×4
5 cm
10 cm
6 cm
4 cm
5 cm
4.5 cm
3. 选一选。
(1)如图,这个平行四边形的面积是( )。
150 cm B. 80 cm C. 120 cm D. 180 cm
C
(2)(易错题)一个平行四边形的底不变,高扩大到原来的2倍,面积( )。
A.不变
B.扩大到原来的2倍
C.扩大到原来的4倍
D.扩大到原来的8倍
B
3. 选一选。
(3)一个平行四边形的底扩大到原来的2倍,高缩小到原来的一半,面积( )。
A.扩大到原来的4倍
B.不变
C.缩小到原来的一半
B
3. 选一选。
3. 选一选。
(4)一块平行四边形菜地,底是450米,高是200米,这块菜地有( )公顷。
A. 9 B. 90 C. 900 D. 90000
(5)一个平行四边形的底扩大到原来的2倍,高不变,面积就扩大到原来的( )倍;如果底和高都扩大到原来的2倍,那么面积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
A
A
B
4. 一个停车位是平行四边形,它的底是 5 米,它的高是 2.5 米,它的面积是多少?
S = ah
= 5×2.5
= 12.5(m2)
答:这个停车位的面积是 12.5 m2。
注意书写格式,结果单位不要忘记。
教材第87页第1题
5. 计算下面平行四边形的面积。
S = ah
= 4×3
= 12(cm2)
S = ah
= 5.2×3.6
= 18.72(cm2)
教材第87页第2题
4 cm
3 cm
5.2 cm
3.6 cm
2 cm
2.4 cm
1.6 cm
3 cm
注意底和高的对应性。
S=ah
5. 计算下面平行四边形的面积。
教材第87页第2题
S = ah
= 2×2.4
= 4.8(cm )
S = ah
= 3×1.6
= 4.8(cm )
方法一:
方法二:
2 cm
2.4 cm
3 cm
S=ah
1.6 cm
6.下表给出的是平行四边形的底和高,计算出每个平行四边形的面积,填在空格里。
底/cm 38 70 6.2 21.5 18 0.9
高/cm 21 15 26 9.8 5.2 0.4
面积/cm2
798
1050
161.2
210.7
93.6
0.36
教材第87页第3题
7.你能想办法求出右面两个平行四边形的面积吗?
提示:自己用刻度尺量出每个平行四边形的底和高,
利用公式求出它们的面积。
教材第87页第4题
8. 有一块麦田的形状是平行四边形。它的底是250 m,高是84 m,共收小麦14.7吨。这块麦田有多少公顷?平均每公顷收小麦多少吨?
麦田面积: 250×84 = 21000(m2)
单位换算: 21000 m2 = 2.1 (公顷)
平均收麦: 14.7÷2.1 = 7(吨)
答:这块麦田有2.1公顷,平均每公顷收小麦7吨。
要求麦田有多少公顷,实际是求这块麦田的面积。
教材第87页第5题
9.在一块底是8 m,高是6 m的平行四边形地里种萝
卜。如果每平方米收萝卜7.5 kg,这块地可收萝卜
多少千克?
8×6=48(m2)
7.5×48=360(kg)
答:这块地可收萝卜360千克。
10. 一块平行四边形的地,底是10.5 m,高是6.4 m,如果用这块地种辣椒,每棵辣椒占地 0.2 m2,这块地一共可以种多少棵辣椒?
这块地的面积:10.5×6.4 = 67.2(m2)
种辣椒棵树: 67.2÷0.2 = 336(棵)
答:这块地一共可以种336棵辣椒。
要求辣椒种植棵数,先要求出这块地的总面积。然后用“总面积÷每棵辣椒的占地面积=种植棵数”即可求解。
平行四边形的面积
×
底
高
长方形的面积 =
×
长
宽
=
S=a×h=a·h=ah
平行四边形的面积=底×高,在利用S=ah求面积时,要用相对应的底和高才能得出正确的结果。
这节课你有什么收获?
