第六单元第6课时 梯形面积(2)(课件)五年级数学上册 最新人教版(共22张PPT)
文档属性
| 名称 | 第六单元第6课时 梯形面积(2)(课件)五年级数学上册 最新人教版(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 19:05:14 | ||
图片预览






文档简介
(共22张PPT)
多边形的面积
6
人教版五年级数学上册
第6课时 梯形的面积(2)
高
下底
上底
高
下底
上底
高
下底
上底
高
梯形
转化
拼接、割补
学过的图形
推导
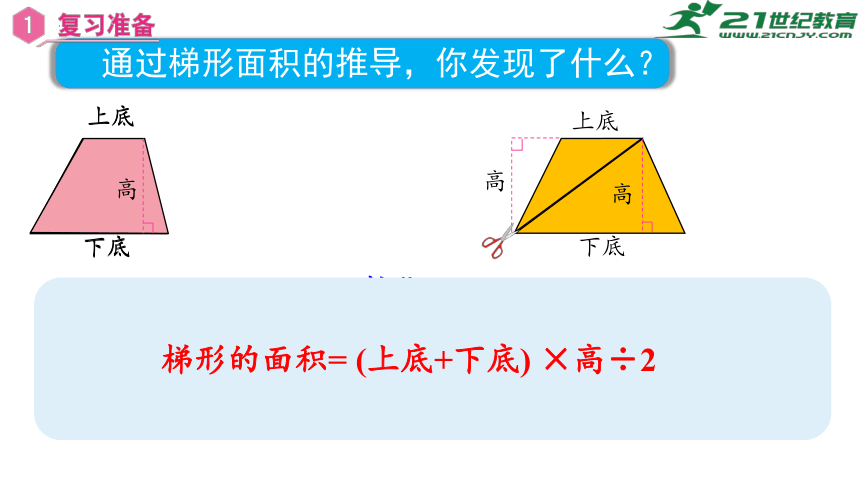
梯形的面积= (上底+下底) ×高÷2
通过梯形面积的推导,你发现了什么?
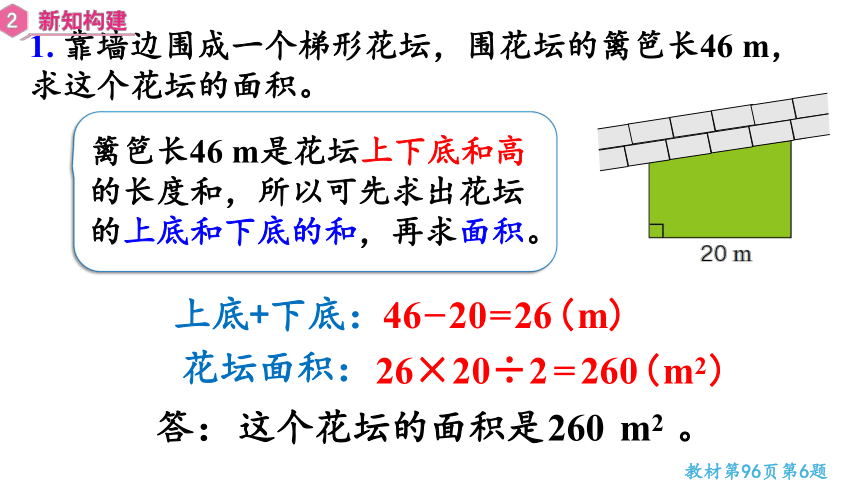
篱笆长46 m是花坛上下底和高的长度和,所以可先求出花坛的上底和下底的和,再求面积。
1. 靠墙边围成一个梯形花坛,围花坛的篱笆长46 m,求这个花坛的面积。
26×20÷2=260(m2)
46 20=26(m)
上底+下底:
花坛面积:
答:
这个花坛的面积是260 m2 。
教材第96页第6题
2.
已知一个梯形的面积是15 cm 。它的上底是 4.5 cm,高是3 cm,下底是多少厘米?
方法一:根据S=(a+b)h÷2,可以得到b=2S÷h-a。
b = 2S÷h-a
= 2×15÷3-4.5
= 10-4.5
= 5.5(cm)
答:下底是5.5厘米。
3 cm
4.5 cm
教材第96页第7题
2.
已知一个梯形的面积是15 cm 。它的上底是 4.5 cm,高是3 cm,下底是多少厘米?
方法二:根据S=(a+b)h÷2列方程。
3 cm
4.5 cm
解:设下底是x厘米。
答:下底是5.5厘米。
(4.5+x)×3÷2=15
4.5+x=15×2÷3
4.5+x=10
x=10 4.5
x=5.5
3. 我们经常见到圆木、钢管等堆成像下图的形状。通常用下面的方法求总根数:
(顶层根数+底层根数)×层数÷2
算出图中圆木的总根数。
这是什么道理?
教材第96页第8题
横截面是个梯形,求总根数的方法是将长度转化为根数,将高转化为层数。
(顶层根数+底层根数)×层数÷2
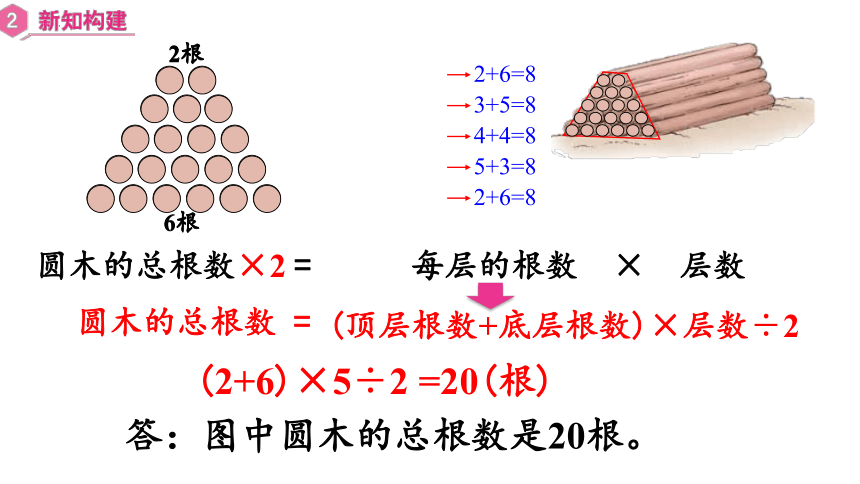
2根
6根
2根
6根
2+6=8
3+5=8
4+4=8
5+3=8
2+6=8
圆木的总根数×2 =
每层的根数 × 层数
圆木的总根数 =
(2+6)×5÷2 =20(根)
答:图中圆木的总根数是20根。
4.在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
教材第96页第11题
在梯形中剪去一个最大的平行四边形,是以梯形的上底长度为底的平行四边形。它的剪法有两种。
4.在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
方法一
梯形的面积-平行四边形的面积
梯形:
(3.5+2)×1.8÷2=4.95(平方厘米)
平行四边形:
2×1.8=3.6(平方厘米)
剩下:4.95-3.6=1.35(平方厘米)
教材第96页第11题
方法二
直接求剩下三角形的面积
(3.5-2)×1.8÷2
=1.5×1.8÷2
=1.35(平方厘米)
4.在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
1. 填一填。
(1)一块梯形土地,上底和高都是400米,下底是上底的2倍,这块地的面积是( )平方米,合( )公顷。
(2)如右图所示,这个直角梯形的面积
是( )平方米。
(3)两个完全一样的直角梯形拼成一个正方形,已知这个正方形的边长是10 cm,则一个直角梯形的面积是( ) 平方厘米。
240000
24
90
50
8 m
12 m
9 m
10 m
(4)一个梯形,面积是7 cm ,上底是3 cm,下底是4 cm,高是( )cm。
(5)下图中的梯形,面积相等的是( )。(把图形的序号填在括号里)
2
①②④
(6)在下面平行线之间画两个梯形,使它们的面积都与阴影部分的面积相等。
(画法不唯一)
2.选一选。
(1)一个梯形的面积是28 dm2,如果上底增加2 dm,下底减少2 dm,高不变,那么新梯形的面积是( )dm2。
A.28 B.14 C.26
A
(2)一个梯形的高不变,上底和下底都扩大到原来的3倍,则面积( )。
A.扩大到原来的3倍 B.扩大到原来的6倍
C.扩大到原来的9倍
A
(3)张浩将梯形ABCD通过割补的方法转化成三角形ABF(过程如图)。已知三角形ABF的面积是24 cm ,则CF的长是( )cm。
A.2 B.4 C.6 D.12
B
3.已知三角形的面积是5.4 dm2,求梯形的面积。
5.4×2÷3=3.6(dm)
(5+5-3.6)×3÷2=9.6(dm2)
答:梯形的面积是9.6 dm2。
4.(易错题)如下图,阴影部分的面积是32 dm2,求梯形的面积。
32×2÷8=8(dm)
(8+12)×8÷2=80(dm2)
答:梯形的面积是80 dm2。
……
……
……
……
……
……
……
……
……
……
……
……
……
76个
152个
40排
5. 一个剧场设置了40排座位,第一排有76个座位,往后逐排比前一排多2个座位,最后一排有152个座位,这个剧场一共设置了多少个座位?
(76+152)×40 ÷ 2=4560(个)
答:这个剧场一共设置了4560个座位。
……
……
……
……
……
……
……
……
……
……
……
……
……
76个
152个
40排
此题可仿照圆木总根数求法公式,用“(第一排座位数+最后一排座位数)×排数÷2” 来求。
6.如图,把梯形的上底延长,使它和下底相等,这时梯形就变成了一个平行四边形,已知梯形的面积是255 cm2,求平行四边形的面积。
255×2÷(10+24)=15(cm)
24×15=360(cm2)
答:平行四边形的面积是360 cm2。
7.一块梯形地,上底是30 m,下底减少10 m变成一个平行四边形,这个平行四边形的面积是1500 m2。原来梯形的面积是多少平方米?
提示:平行四边形的底就是梯形的上底,高与梯形的高相等。
(30+30+10)×(1500÷30)÷2=1750(m2)
答:原来梯形的面积是1750 m2。
在求梯形的面积时,题中有些条件没有直接给出,需结合实际认真分析,观察图形各部分之间和已知条件的关系,再进行求解。
多边形的面积
6
人教版五年级数学上册
第6课时 梯形的面积(2)
高
下底
上底
高
下底
上底
高
下底
上底
高
梯形
转化
拼接、割补
学过的图形
推导
梯形的面积= (上底+下底) ×高÷2
通过梯形面积的推导,你发现了什么?
篱笆长46 m是花坛上下底和高的长度和,所以可先求出花坛的上底和下底的和,再求面积。
1. 靠墙边围成一个梯形花坛,围花坛的篱笆长46 m,求这个花坛的面积。
26×20÷2=260(m2)
46 20=26(m)
上底+下底:
花坛面积:
答:
这个花坛的面积是260 m2 。
教材第96页第6题
2.
已知一个梯形的面积是15 cm 。它的上底是 4.5 cm,高是3 cm,下底是多少厘米?
方法一:根据S=(a+b)h÷2,可以得到b=2S÷h-a。
b = 2S÷h-a
= 2×15÷3-4.5
= 10-4.5
= 5.5(cm)
答:下底是5.5厘米。
3 cm
4.5 cm
教材第96页第7题
2.
已知一个梯形的面积是15 cm 。它的上底是 4.5 cm,高是3 cm,下底是多少厘米?
方法二:根据S=(a+b)h÷2列方程。
3 cm
4.5 cm
解:设下底是x厘米。
答:下底是5.5厘米。
(4.5+x)×3÷2=15
4.5+x=15×2÷3
4.5+x=10
x=10 4.5
x=5.5
3. 我们经常见到圆木、钢管等堆成像下图的形状。通常用下面的方法求总根数:
(顶层根数+底层根数)×层数÷2
算出图中圆木的总根数。
这是什么道理?
教材第96页第8题
横截面是个梯形,求总根数的方法是将长度转化为根数,将高转化为层数。
(顶层根数+底层根数)×层数÷2
2根
6根
2根
6根
2+6=8
3+5=8
4+4=8
5+3=8
2+6=8
圆木的总根数×2 =
每层的根数 × 层数
圆木的总根数 =
(2+6)×5÷2 =20(根)
答:图中圆木的总根数是20根。
4.在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
教材第96页第11题
在梯形中剪去一个最大的平行四边形,是以梯形的上底长度为底的平行四边形。它的剪法有两种。
4.在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
方法一
梯形的面积-平行四边形的面积
梯形:
(3.5+2)×1.8÷2=4.95(平方厘米)
平行四边形:
2×1.8=3.6(平方厘米)
剩下:4.95-3.6=1.35(平方厘米)
教材第96页第11题
方法二
直接求剩下三角形的面积
(3.5-2)×1.8÷2
=1.5×1.8÷2
=1.35(平方厘米)
4.在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
1. 填一填。
(1)一块梯形土地,上底和高都是400米,下底是上底的2倍,这块地的面积是( )平方米,合( )公顷。
(2)如右图所示,这个直角梯形的面积
是( )平方米。
(3)两个完全一样的直角梯形拼成一个正方形,已知这个正方形的边长是10 cm,则一个直角梯形的面积是( ) 平方厘米。
240000
24
90
50
8 m
12 m
9 m
10 m
(4)一个梯形,面积是7 cm ,上底是3 cm,下底是4 cm,高是( )cm。
(5)下图中的梯形,面积相等的是( )。(把图形的序号填在括号里)
2
①②④
(6)在下面平行线之间画两个梯形,使它们的面积都与阴影部分的面积相等。
(画法不唯一)
2.选一选。
(1)一个梯形的面积是28 dm2,如果上底增加2 dm,下底减少2 dm,高不变,那么新梯形的面积是( )dm2。
A.28 B.14 C.26
A
(2)一个梯形的高不变,上底和下底都扩大到原来的3倍,则面积( )。
A.扩大到原来的3倍 B.扩大到原来的6倍
C.扩大到原来的9倍
A
(3)张浩将梯形ABCD通过割补的方法转化成三角形ABF(过程如图)。已知三角形ABF的面积是24 cm ,则CF的长是( )cm。
A.2 B.4 C.6 D.12
B
3.已知三角形的面积是5.4 dm2,求梯形的面积。
5.4×2÷3=3.6(dm)
(5+5-3.6)×3÷2=9.6(dm2)
答:梯形的面积是9.6 dm2。
4.(易错题)如下图,阴影部分的面积是32 dm2,求梯形的面积。
32×2÷8=8(dm)
(8+12)×8÷2=80(dm2)
答:梯形的面积是80 dm2。
……
……
……
……
……
……
……
……
……
……
……
……
……
76个
152个
40排
5. 一个剧场设置了40排座位,第一排有76个座位,往后逐排比前一排多2个座位,最后一排有152个座位,这个剧场一共设置了多少个座位?
(76+152)×40 ÷ 2=4560(个)
答:这个剧场一共设置了4560个座位。
……
……
……
……
……
……
……
……
……
……
……
……
……
76个
152个
40排
此题可仿照圆木总根数求法公式,用“(第一排座位数+最后一排座位数)×排数÷2” 来求。
6.如图,把梯形的上底延长,使它和下底相等,这时梯形就变成了一个平行四边形,已知梯形的面积是255 cm2,求平行四边形的面积。
255×2÷(10+24)=15(cm)
24×15=360(cm2)
答:平行四边形的面积是360 cm2。
7.一块梯形地,上底是30 m,下底减少10 m变成一个平行四边形,这个平行四边形的面积是1500 m2。原来梯形的面积是多少平方米?
提示:平行四边形的底就是梯形的上底,高与梯形的高相等。
(30+30+10)×(1500÷30)÷2=1750(m2)
答:原来梯形的面积是1750 m2。
在求梯形的面积时,题中有些条件没有直接给出,需结合实际认真分析,观察图形各部分之间和已知条件的关系,再进行求解。
