4.4.3不同函数的增长的差异 课件(共18张PPT)
文档属性
| 名称 | 4.4.3不同函数的增长的差异 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 516.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 08:15:44 | ||
图片预览





文档简介
(共18张PPT)
4.4.3不同函数增长的差异
学习目标
1.掌握常见增长函数的定义、图象、性质,并体会其增长的快慢.(重点)
2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的性质的比较,培养数学建模和数学运算等核心素养.(难点)
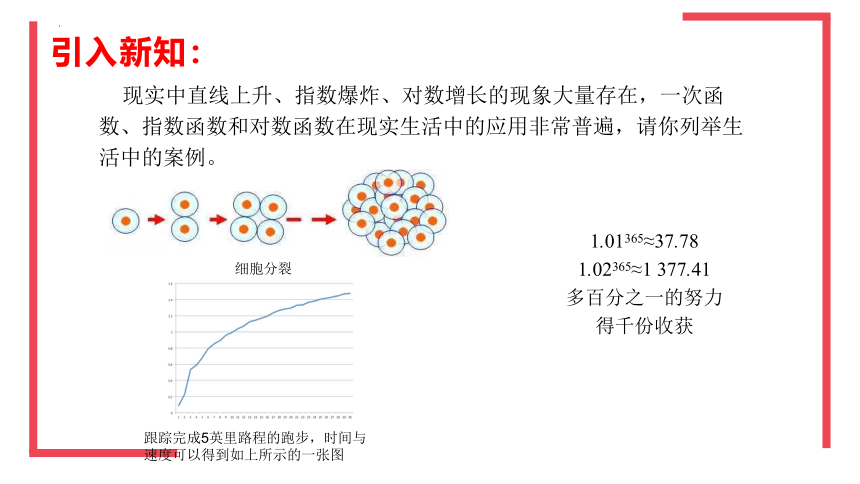
引入新知:
现实中直线上升、指数爆炸、对数增长的现象大量存在,一次函数、指数函数和对数函数在现实生活中的应用非常普遍,请你列举生活中的案例。
跟踪完成5英里路程的跑步,时间与速度可以得到如上所示的一张图
细胞分裂
1.01365≈37.78
1.02365≈1 377.41
多百分之一的努力
得千份收获
思考:
1. 三种函数模型的性质?
2. 三种函数的增长速度比较?
1.三种函数模型的性质
2.三种函数的增长速度比较
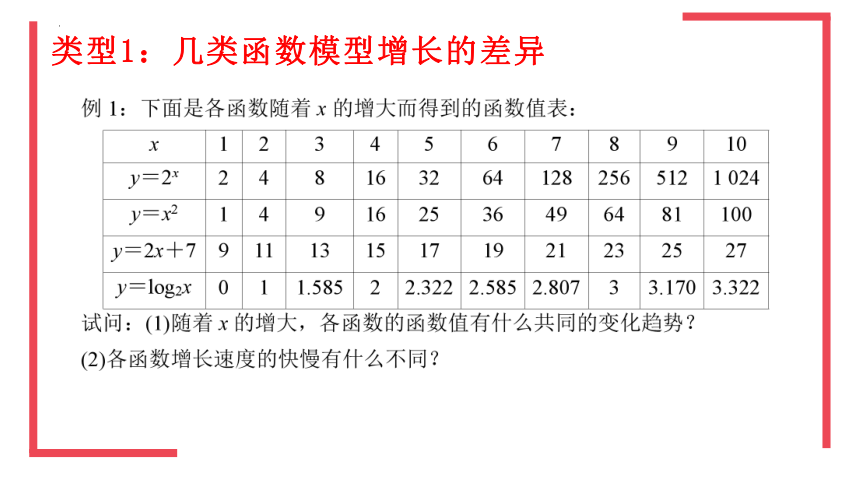
(1)在区间(0,+∞)上,函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是增函数,但增长速度不同.
(2)在区间(0,+∞)上随着x的增大,函数y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而函数y=logax(a>1)的增长速度则会越来越慢.
(3)存在一个x0,使得当x>x0时,有logax类型1:几类函数模型增长的差异
类型2:比较函数增长的差异
例2: 函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1(1)指出图中曲线C1,C2分别对应的函数;
(2)结合函数图象,判断f(6),g(6),f(2 019),g(2 019)的大小.
解:(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)因为f(1)>g(1),f(2)g(10),所以1所以x1<6x2,从图象上可以看出,当x1当x>x2时,f(x)>g(x),所以f(2 019)>g(2 019).
因为g(2 019)>g(6),
所以f(2 019)>g(2 019)>g(6)>f(6).
1.当a>1时,有下列结论:
①指数函数y=ax,当a越大时,其函数值的增长越快;
②指数函数y=ax,当a越小时,其函数值的增长越快;
③对数函数y=logax,当a越大时,其函数值的增长越快;
④对数函数y=logax,当a越小时,其函数值的增长越快.
其中正确的结论是( )
A.①③ B.①④ C.②③ D.②④
练习:
归纳总结:
根据图象判断增长型的指数函数、一次函数时,通常是观察函数图象上升的快慢,即随着自变量的增大,图象最“陡”的函数是指数函数.
类型3:实际问题的解决
例4.某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资的函数模型为y=k1x,B产品的利润与投资的函数模型为y=k2xα(利润和投资的单位为百万元),其关系分别如图①,图②所示.
(1)分别求出A,B两种产品的利润与投资的函数关系式;
(2)该企业已筹集到资金1千万元,并准备全部投入到A,B两种产品的生产中,问怎样分配这1千万元,才能使企业获得最大利润,其最大利润为多少 (精确到万元)
故投资A产品844万元,投资B产品156万元时,总利润最大,最大值约为578万元.
练习:
直线上升、指数爆炸、对数增长对于直线y=kx+b(k≥0)、指数函数y=ax(a>1)、对数函数y=logax(a>1),当自变量变得很大时,指数函数比一次函数增长得快,一次函数比对数函数增长得快,并且直线上升,其增长量固定不变.
4.4.3不同函数增长的差异
学习目标
1.掌握常见增长函数的定义、图象、性质,并体会其增长的快慢.(重点)
2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的性质的比较,培养数学建模和数学运算等核心素养.(难点)
引入新知:
现实中直线上升、指数爆炸、对数增长的现象大量存在,一次函数、指数函数和对数函数在现实生活中的应用非常普遍,请你列举生活中的案例。
跟踪完成5英里路程的跑步,时间与速度可以得到如上所示的一张图
细胞分裂
1.01365≈37.78
1.02365≈1 377.41
多百分之一的努力
得千份收获
思考:
1. 三种函数模型的性质?
2. 三种函数的增长速度比较?
1.三种函数模型的性质
2.三种函数的增长速度比较
(1)在区间(0,+∞)上,函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是增函数,但增长速度不同.
(2)在区间(0,+∞)上随着x的增大,函数y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而函数y=logax(a>1)的增长速度则会越来越慢.
(3)存在一个x0,使得当x>x0时,有logax
类型2:比较函数增长的差异
例2: 函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1
(2)结合函数图象,判断f(6),g(6),f(2 019),g(2 019)的大小.
解:(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)因为f(1)>g(1),f(2)
因为g(2 019)>g(6),
所以f(2 019)>g(2 019)>g(6)>f(6).
1.当a>1时,有下列结论:
①指数函数y=ax,当a越大时,其函数值的增长越快;
②指数函数y=ax,当a越小时,其函数值的增长越快;
③对数函数y=logax,当a越大时,其函数值的增长越快;
④对数函数y=logax,当a越小时,其函数值的增长越快.
其中正确的结论是( )
A.①③ B.①④ C.②③ D.②④
练习:
归纳总结:
根据图象判断增长型的指数函数、一次函数时,通常是观察函数图象上升的快慢,即随着自变量的增大,图象最“陡”的函数是指数函数.
类型3:实际问题的解决
例4.某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资的函数模型为y=k1x,B产品的利润与投资的函数模型为y=k2xα(利润和投资的单位为百万元),其关系分别如图①,图②所示.
(1)分别求出A,B两种产品的利润与投资的函数关系式;
(2)该企业已筹集到资金1千万元,并准备全部投入到A,B两种产品的生产中,问怎样分配这1千万元,才能使企业获得最大利润,其最大利润为多少 (精确到万元)
故投资A产品844万元,投资B产品156万元时,总利润最大,最大值约为578万元.
练习:
直线上升、指数爆炸、对数增长对于直线y=kx+b(k≥0)、指数函数y=ax(a>1)、对数函数y=logax(a>1),当自变量变得很大时,指数函数比一次函数增长得快,一次函数比对数函数增长得快,并且直线上升,其增长量固定不变.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
