2023届高三数学二轮复习-最近三年高考数学数列真题(PDF版含解析)
文档属性
| 名称 | 2023届高三数学二轮复习-最近三年高考数学数列真题(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 435.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 13:16:19 | ||
图片预览




文档简介
近三年高考数学数列真题合集
等差数列通项与前 n 项和求解
1.(2022上海)已知等差数列{an}的公差不为零,Sn为其前 n项和,若 S5 0,则 Si (i 0,
1,2, ,100)中不同的数值有__________个.
2.(2022全国乙卷文)记 Sn为等差数列 an 的前 n项和.若 2S3 3S2 6,则公差
d __________.
3.(2021 上海春季)已知等差数列{an}的首项为 3,公差为 2,则 a10 __________.
4.(2021 北京)已知{an}是各项为整数的递增数列,且 a1 3,若a1 a2 a3 an 100,
则 n的最大值为( )
A.9 B.10 C.11 D.12
5.(2020海南)将数列{2n 1}与{3n 2}的公共项从小到大排列得到数列{an},则{an}的
前 n项和为__________.
6. (2020 上 海 )已 知 数 列 {an} 是 公 差 不为 零 的 等 差 数 列, 且 a1 a10 a9 , 则
a1 a2 a9 __________.
a10
7.(2020新课标Ⅱ理)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心
有一块圆形石板(称为天心石),环绕天心石砌 9块扇面形石板构成第一环,向外每环依次
增加 9块.下一层的第一环比上一层的最后一环多 9块,向外每环依次也增加 9块.已知每
层环数相同,且下层比中层多 729块,则三层共有扇面形石板(不含天心石)( )
1/18
A.3699块 B.3474块 C.3402块 D.3339块
a
8.(2020 浙江)已知等差数列{an}的前 n项和 Sn ,公差 d 0,且 1 1.记 b1 S2 ,d
bn 1 S2n 2 S2n , n N *,下列等式不可能成立的是( )
A. 2a4 a2 a6 B. 2b4 b2 b6 C
2
.a4 a2a8 D b
2
. 4 b2b8
等比数列通项与前 n 项和求解
1.(2022全国乙卷文 10理 8)已知等比数列 an 的前 3项和为 168, a2 a5 42,则
a6 ( )
A. 14 B. 12 C. 6 D. 3
2.(2021 上海)已知{an}为无穷等比数列,a1 3,an 的各项和为 9,bn a2n,则数列{bn}
的各项和为__________.
3.(2021 文科甲卷)记 Sn为等比数列{an}的前 n项和.若 S2 4,S4 6,则 S6 ( )
A.7 B.8 C.9 D.10
4.(2020 江苏)设{an}是公差为 d 的等差数列,{bn}是公比为 q的等比数列.已知数列
{an bn}的前 n项和 Sn n
2 n 2n 1(n N*),则 d q的值是__________.
2/18
5.(2020新课标Ⅱ理)数列{an}中,a
15 5
1 2,am n aman .若ak 1 ak 2 ak 10 2 2 ,
则 k ( )
A.2 B.3 C.4 D.5
数列的单调性与最值
1. (2022北京)设 an 是公差不为 0的无穷等差数列,则“ an 为递增数列”是“存在正
整数 N0 ,当 n N0 时, an 0”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
2.(2022上海春考)已知等比数列{an}的前 n项和为 Sn,前 n项积为Tn ,则下列选项判断
正确的是( )
A.若 S2022 S2021 ,则数列{an}是递增数列
B.若T2022 T2021,则数列{an}是递增数列
C.若数列{Sn}是递增数列,则 a2022 a2021
D.若数列{Tn}是递增数列,则 a2022 a2021
3.(2021 甲卷)等比数列{an}的公比为 q,前 n项和为 Sn.设甲:q 0,乙:{Sn}是递
增数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
4.(2020北京)在等差数列{an}中,a1 9,a5 1.记Tn a1a2 an (n 1,2, ),
3/18
则数列{Tn} ( )
A.有最大项,有最小项 B.有最大项,无最小项
C.无最大项,有最小项 D.无最大项,无最小项
数列与实际生活情境结合
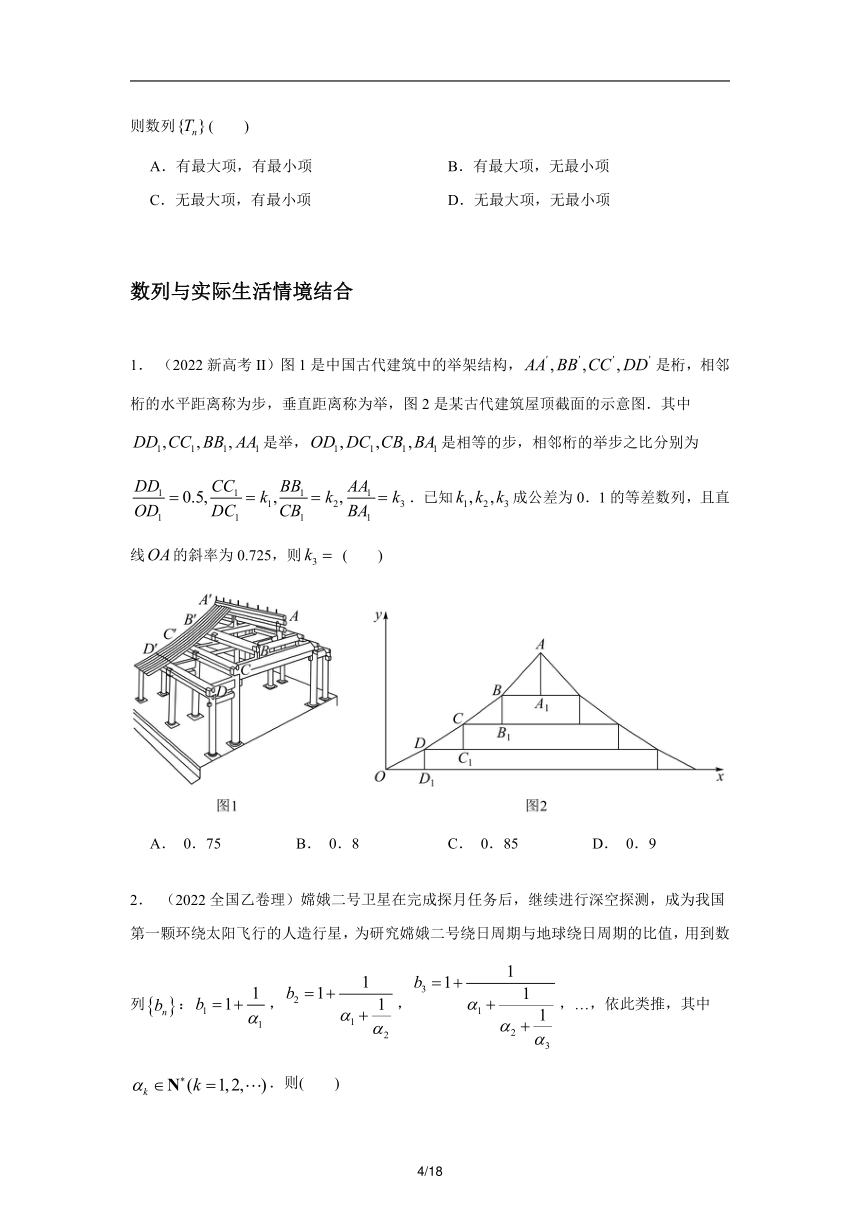
1. (2022新高考 II 1 )图 是中国古代建筑中的举架结构,AA ,BB ,CC ,DD 是桁,相邻
桁的水平距离称为步,垂直距离称为举,图 2是某古代建筑屋顶截面的示意图.其中
DD1,CC1,BB1, AA1是举,OD1,DC1,CB1 ,BA1是相等的步,相邻桁的举步之比分别为
DD1 0.5, CC1 k ,BB1 k , AA 1 1 k .已知 k ,k ,k 成公差为 0.1的等差数列,且直OD1 DC1 CB
2 BA 3 1 2 31 1
线OA的斜率为 0.725,则 k3 ( )
A. 0.75 B. 0.8 C. 0.85 D. 0.9
2. (2022全国乙卷理)嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国
第一颗环绕太阳飞行的人造行星,为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数
1
1 b 1 b 1 b 1 2 1
3
列 bn : 1 , 1 ,
1
1 ,1 …
,依此类推,其中
1 1 2 2 3
N k (k 1,2, ).则( )
4/18
A. b1 b5 B. b3 b8 C. b6 b2 D. b4 b7
3.(2021 北京)《中国共产党党旗党徽制作和使用的若干规定》指出,中国共产党党旗为旗
面缀有金黄色党徽图案的红旗,通用规格有五种.这五种规格党旗的长 a1, a2, a3, a4,
a5 (单位:cm)成等差数列,对应的宽为b1,b2,b3,b4,b5(单位:cm ),且长与宽
之比都相等.已知 a1 288, a5 96,b1 192,则b3 ( )
A.64 B.96 C.128 D.160
4.(2021 新高考Ⅰ)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴
把纸对折.规格为 20dm 12dm 的长方形纸,对折 1 次共可以得到 10dm 12dm,
20dm 6dm 两种规格的图形,它们的面积之和 S1 240dm
2
,对折 2 次共可以得到
5dm 12dm,10dm 6dm,20dm 3dm 2三种规格的图形,它们的面积之和 S2 180dm ,
以此类推.则对折 4次共可以得到不同规格图形的种数为__________;如果对折 n次,那么
n
Sk __________ dm2 .
k 1
数列与新定义
1.(2021 新高考Ⅱ 0 1)设正整数 n a0 2 a1 2 ak 1 2
k 1 a kk 2 ,其中 ai {0,1},
记 (n) a0 a1 ak ,则( )
A. (2n) (n) B. (2n 3) (n) 1
C. (8n 5) (4n 3) D n. (2 1) n
2.(2020 新课标Ⅱ理) 0 1周期序列在通信技术中有着重要应用.若序列 a1a2 an 满足
ai {0,1}(i 1,2, ),且存在正整数m,使得 ai m ai (i 1,2, )成立,则称其
为0 1周期序列,并称满足 ai m ai (i 1,2 )的最小正整数m为这个序列的周期.对于
5/18
m
周期为m的 0 1序列 a1a2 an ,C(k)
1
aiai k (k 1,2, ,m 1)是描述其m i 1
性质的重要指标,下列周期为 5的0 1序列中,满足C(k) 1 (k 1,2,3,4)的序列是( )
5
A.11010 B.11011 C.10001 D.11001
数列综合小题
1.(2022北京)己知数列 an 各项均为正数,其前 n项和 Sn满足 an Sn 9(n 1,2, ).给
出下列四个结论:
① an 的第 2项小于 3; ② an 为等比数列;
a a 1③ n 为递减数列; ④ n 中存在小于 的项.100
其中所有正确结论的序号是__________.
2.(2021 上海)已知 ai N *(i 1,2, ,9)对任意的 k N *(2 k 8),ak ak 1 1
或 ak ak 1 1中有且仅有一个成立,a1 6,a9 9,则 a1 a9 的最小值为__________.
6/18
近三年高考数学数列真题合集解析
等差数列通项与前 n 项和求解
1.【解答】由等差数列对称性可知:
S0 S5 0, S2 S3 , S1 S4,
其余各项均不相等,
Si (i 0,1,2 ,100)中不同的数值有:101 3 98个.
故答案为 98.
2.【解答】由 2S3 3S2 6可得 2 a1 a2+a3 3 a1 a2 6,
化简得 2 a1+2d 2a1 d 6,
解得 d 2.
故答案为 2.
3.【解答】因为等差数列{an}的首项为 3,公差为 2,
则 a10 a1 9d 3 9 2 21.
故答案为 21.
4.【解答】数列{an}是递增的整数数列,
n要取最大,后一个比前一个要大 1,
a1 3,
an n 2,
S (3 n 2)n 5n n
2
则 n ,2 2
试数取 n 11时, S11 88, a11 13,
7/18
100 S12 12 a11 13,
此时显然 n继续增大,则 a12 a11,不满足题意,
所以 n 11为最大值.
故选C.
5.【解答】数列{2n 1}与{3n 2}首项均为 1,此后每变大 6,即为二者公共项,
所以数列{an}是以 1为首项、以 6为公差的等差数列,
n(n 1)
故它的前 n项和为n 1 6 3n2 2n,
2
2
故答案为3n 2n.
6.【解答】根据题意,因为 a1 a10 a9 ,即 a1 a1 9d a1 8d ,
变形可得 a1 d,
9a 9 8da1 a2 a 1
9 2 9a1 36d 9d 36d 27所以 .
a10 a1 9d a1 9d d 9d 8
27
故答案为 .
8
7.【解答】设每一层有 n环,由题意可知,从内到外每环上扇面形石板数之间构成等差数列,
上层中心的首项为 a1 9,且公差 d 9,
由等差数列前 n项和的性质:
S 2n, S2n Sn , S3n S2n 成等差数列,且 (S3n S2n ) (S2n Sn ) n d,
n2所以 d 729,
则 n 9,
S S 27 9 27 26则三层共有扇面形石板 3n 27 9 3402块,2
故选C.
8.【解答】在等差数列{an}中, an a1 (n 1)d ,
8/18
a2 a1 d , a4 a1 3d, a8 a1 7d ,
而 2a4 a2 a6 ,根据等差数列的性质知 A正确,
bn 1 S2n 2 S2n,
b2 S4 S2 a3 a4 ,
b4 S8 S6 a7 a8 ,
b6 S12 S10 a11 a12 ,
所以对 2b4 b2 b6 ,即 2(a7 a8) a3 a4 a11 a12 (a3 a12 ) (a4 a11) ,
可知成立, B正确,
对C a2.若 4 a
2
2a8,则 (a1 3d) (a1 d)(a1 7d),
a2 6a d 9d 2 2即 1 1 a1 8a1d 7d
2 2
,得 a1d d ,
d a 0, a1 d ,符合 1 1,所以C正确;d
对D b2.若 4 b
2
2b8,则 (a7 a8) (a3 a4 )(a15 a16 ),
2
即 4a1 52a1d 169d
2 4a21 68a
2
1d 145d ,得16a1d 24d
2
,
d 0 2a a , 1 3d ,不符合 1 1,D错误;d
故选D.
等比数列通项与前 n 项和求解
1.【解答】设等比数列 an 的公比为 q,q 0,且显然 q 1,
a 1 q3 a 96
a1 a a
1 1
则 2 3
168
1 q ,解得 1 ,
q
a2 a5 a q a
4
1 1q 42 2
所以 a 5 .6 a1q 3
故选 D.
9/18
2.【解答】设{an}的公比为 q,
由 a1 3
3
, an 的各项和为 9,可得 9,1 q
q 2 2解得 ,所以 an 3 ( )
n 1
,
3 3
bn a2n 3 (
2)2n 1,
3
4
可得数列{bn}是首项为 2,公比为 的等比数列,9
{b } 2 18则数列 n 的各项和为 4 .1 5
9
18
故答案为 .
5
3.【解答】 Sn 为等比数列{an}的前 n项和, S2 4, S4 6,
由等比数列的性质,可知 S2, S4 S2 , S6 S4 成等比数列,
4,2, S6 6成等比数列,
22 4(S6 6),解得 S6 7.
故选 A.
4.【解答】依题意,数列{an}的通项公式 an a1 (n 1)d ,
d 2
所以其前 n项和 n (a d )n,
2 1 2
当{bn}中,当公比 q 1时,其前 n项和 nb1,
而{an b }
d 2 d 2 n
n 的前 n项和 Sn n (a1 )n nb1 n n 2 1(n N*),显然没有出2 2
现 2n,所以 q 1,
n
{b } b (q 1) b q
n b
则 n 的前 n项和为 1 1 1 ,q 1 q 1 q 1
S d n2 (a d
n
所以 n 1 )n
b
1
q b
1 n2 n 2 n 1(n N*) ,
2 2 q 1 q 1
10/18
d
1
2
a
d
1 1
由两边对应项相等可得: 2 解得: d 2, a1 0,q 2,b1 1,
q 2
b1 1
q 1
所以 d q 4,
故答案为 4
5.【解答】由 a1 2,且 am n aman ,
取m 1,得 an 1 a1an 2an ,
a
n 1 2,
an
则数列{an}是以 2为首项,以 2为公比的等比数列,
a 2 2k 2k 1则 k 1 ,
2k 1 10
ak 1 ak 2 a
(1 2 )
211 k 2k 1 215 5k 10 2 ,1 2
k 1 5,即 k 4.
故选C.
数列的单调性与最值
1.【解答】设等差数列 an 的公差为 d ,则 d 0,记 x 为不超过 x的最大整数.
若 an 为单调递增数列,则 d 0,
若 a1 0,则当 n 2时, an a1 0;若 a1 0,则 an a1 n 1 d,
a a a1 a 由 n 11 n 1 d 0可得 n 1 ,取 N0 1 1,则当 n N0 时, ad d n
0,
11/18
所以,“ an 是递增数列” “存在正整数 N0 ,当 n N0 时, an 0 ”;
若存在正整数 N0 ,当 n N0 时, an 0,取 k N 且 k N0, ak 0,
假设 d 0,令 a a n k d 0 a a可得 n k k ,且 k kn k k ,d d
a
当 n k
k
1时, an 0,与题设矛盾,假设不成立,则 d 0,即数列 an 是递增 d
数列.
所以,“ an 是递增数列” “存在正整数 N0 ,当 n N0 时, an 0 ”.
所以,“ an 是递增数列”是“存在正整数N0 ,当 n N0 时, an 0 ”的充分必要条件.
故选 C.
2.【解答】如果数列 a1 1,公比为 2,满足 S2022 S2021 ,但是数列{an}不是递增数列,
所以 A不正确;
1
如果数列 a1 1,公比为 ,满足T2 2022
T2021 ,但是数列{an}不是递增数列,所以 B不
正确;
1 1 ( ) n1 1
如果数列 a1 1,公比为 , S 2n 1 2(1 n ),数列{Sn}是递增数列,但是2 2
2
a2022 a2021,所以C不正确;
数列{Tn}是递增数列,可知Tn Tn 1,可得 an 1,所以 q 1,可得 a2022 a2021正确,所
以D正确;
故选D.
3.【解答】若 a1 1,q 1,则 Sn na1 n,则{Sn}是递减数列,不满足充分性;
S a1 nn (1 q ),1 q
S a1 n 1则 n 1 (1 q ),1 q
12/18
S S a 1 (q nn 1 n q
n 1) a n
1 q 1
q ,
若{Sn}是递增数列,
Sn 1 Sn a
n
1q 0,
则 a1 0, q 0,
满足必要性,
故甲是乙的必要条件但不是充分条件,
故选 B.
a a 1 ( 9)
4.【解答】设等差数列{an}的公差为 d ,由 a 5 11 9,a5 1,得d 2,5 1 4
an 9 2(n 1) 2n 11.
由 an 2n 11
11
0,得 n ,而 n N *,
2
可知数列{an}是单调递增数列,且前 5项为负值,自第 6项开始为正值.
可知T1 9 0,T2 63 0,T3 315 0,T4 945 0为最大项,
自T5起均小于 0,且逐渐减小.
数列{Tn}有最大项,无最小项.
故选 B.
数列与实际生活情境结合
1.【解答】设OD1 DC1 CB1 BA1 1,则CC1 k1,BB1 k2 ,AA1 k3 ,
DD CC BB AA
依题意,有 k3 0.2 k1,k3 0.1 k2 ,且
1 1 1 1 0.725,
OD1 DC1 CB1 BA1
0.5 3k3 0.3所以 0.725,故 k3 0.9,4
故选 D
13/18
2.【解答】因为 N*k k 1,2, ,
1
1 1
所以 1 1 ,
1 ,得到
1 b1 b2
,
2 1 2
11
1
同理 1 1 ,可得b2 b3 ,2 b1 b32 3
1 1
1 ,
1 1
1
1 1 1
又因为 2 2 2 2 ,
1 133 34 4
故b2 b4,b3 b4;
以此类推,可得b1 b3 b5 b7 …,b7 b8,故 A错误;
b1 b7 b8,故 B错误;
1 1
2 12 ,得b2 b6,故 C错误;
13 … 6
1 11 1
12
1
2 … ,得 ,故 正确.
1 1
b4 b7 D
3 6 4 7
故选 D.
3.【解答】{an}和{b }
a
n 是两个等差数列,且
k (1 k 5)是常值,由于 a1 288,a5 96,bk
a
故 a 1 a53 192,2
a3 a1 288 3由于
b3 b1 192 2
所以b3 128.
14/18
a1 a5 b a b另 ,解得: 5 1 64
b1 b
5
5 a1
故:b b1 b3 5 128.2
故选C.
20dm 3 dm,10dm 3 dm,5dm 3dm, 5 dm 6dm 54.【解答】易知有 , dm 12dm,共
4 2 2 4
5种规格;
k k 1 240 S 240(k 1)由题可知,对折 次共有 种规格,且面积为
2k
,故 k ,2k
n n k 1 n S k 1 1
n k 1
则 k 240 ,记T 2k n 2k ,则 T ,k 1 k 1 k 1 2 n k 1 2k 1
1 nT k 1
n
k 1
n 1 k 2 n 1 k 1 n 1
n 2 2k
2k 1
1 ( k 1 k 1 ) 2 n 1k 1 k 1 k 1 k 1 2 2
1 (1 1 n 1 )
1 n 1 3 n 3 4 21 n 1 ,1 2 2 2
n 1
2
n 3
Tn 3 2n
,
n
Sk 240(3 n 3 n ).
k 1 2
故答案为 5; 240(3 n 3 ).
2n
数列与新定义
1 1 2 k.【解答】 2n a0 2 a1 2 ak 1 2 ak 2
k 1
,
(2n) (n) a0 a1 ak , A对;
当 n 2 0时,2n 3 7 1 2 1 21 1 22, (7) 3 0 1. 2 0 2 1 2 , (2)
0 1 1, (7) (2) 1, B错;
15/18
8n 5 a0 2
3 a1 2
4 a 2k 3k 5 1 2
0 1 22 a 230 a1 2
4 ak 2
k 3
,
(8n 5) a0 a1 a k 2 ,
4n 3 a 22 a 23 a 2k 2 3 1 20 1 21 a 22 a 23 a 2k 20 1 k 0 1 k
(4n 3) a0 a1 a k 2 (8n 5) . C 对;
2n 1 1 20 1 21 1 2n 1, (2n 1) n, D对.
故选 ACD.
2.【解答】对于 A选项:序列 11010 11010
C 1
5 1
(1) aiai 1 (1 0 0 0 0) 1 ,5 i 1 5 5
5
C 1 1(2) aiai 2 (0 1 0 1 0) 2 1 1 ,不满足C(k) (k 1,2,3, 4),5 i 1 5 5 5 5
故排除 A;
对于 B选项:序列 11011 11011
1 5C 1(1) a a (1 0 0 1 1) 3 1 ,不满足条件,排除;
5 i i 1i 1 5 5 5
对于C选项:序列 10001 10001 10001
1 5C(1) a a 1 1
5 i i 1 (0 0 0 0 1) ,i 1 5 5
C 1
5
(2) a 1iai 2 (0 0 0 0 0) 0,5 i 1 5
1 5C a a 1(3) i i 3 (0 0 0 0 0) 0,5 i 1 5
5
C 1 1 1(4) aiai 4 (1 0 0 0 0) ,符合条件,5 i 1 5 5
对于D选项:序列 11001 11001
16/18
1 5C a a 1 (1 2 1(1) i i 1 0 0 0 1) 不满足条件.5 i 1 5 5 5
故选C.
数列综合小题
1.【解答】由题意可知, n N , an 0,
当 n 1时, a2 9,可得 a1 3;1
9
当 n 2时,由 Sn 可得 S
9 9 9
a n 1
,两式作差可得 a
a n
,
n n 1 an an 1
9 9 9
所以, an,则 a2 3,整理可得a22 3a2 9 0,an 1 an a2
因为 a 0,解得a 3 5 32 3,①对;2 2
2
假设数列 an 为等比数列,设其公比为 q,则 a2 ,即
9 81 ,
2 a1a3 S
2 S1S3
所以, S 22 S S ,可得 a
2 1 q 2 a2 1 q q2 ,解得q 0,不合乎题意,1 3 1 1
故数列 an 不是等比数列,②错;
9 9 9 a a
当 n 2时,a n 1 n
n 0,可得 a a ,所以,数列 a 为递减数an a n n 1 nn 1 anan 1
列,③对;
1 1
假设对任意的 n N ,a ,则n S100000 100000 1000,100 100
9 9 1
所以, a100000 ,与假设矛盾,假设不成立,④对.S100000 1000 100
故答案为①③④.
2.【解答】设bk ak 1 ak ,由题意可得,bk ,bk 1恰有一个为 1,
17/18
如果b1 b3 b5 b7 b9 1,那么 a1 6, a2 7, a3 1, a4 a3 1 2,
同样也有, a5 1, a6 a5 1 2, a7 1, a8 a7 1 2,
全部加起来至少是6 7 1 2 1 2 1 2 9 31;
如果b2 b4 b6 b8 1,那么 a8 8, a2 1, a3 a2 1 2,
同样也有, a4 1, a5 2, a6 1, a7 2,
全部加起来至少是6 1 2 1 2 1 2 8 9 32,
综上所述,最小应该是 31.
故答案为 31.
18/18
等差数列通项与前 n 项和求解
1.(2022上海)已知等差数列{an}的公差不为零,Sn为其前 n项和,若 S5 0,则 Si (i 0,
1,2, ,100)中不同的数值有__________个.
2.(2022全国乙卷文)记 Sn为等差数列 an 的前 n项和.若 2S3 3S2 6,则公差
d __________.
3.(2021 上海春季)已知等差数列{an}的首项为 3,公差为 2,则 a10 __________.
4.(2021 北京)已知{an}是各项为整数的递增数列,且 a1 3,若a1 a2 a3 an 100,
则 n的最大值为( )
A.9 B.10 C.11 D.12
5.(2020海南)将数列{2n 1}与{3n 2}的公共项从小到大排列得到数列{an},则{an}的
前 n项和为__________.
6. (2020 上 海 )已 知 数 列 {an} 是 公 差 不为 零 的 等 差 数 列, 且 a1 a10 a9 , 则
a1 a2 a9 __________.
a10
7.(2020新课标Ⅱ理)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心
有一块圆形石板(称为天心石),环绕天心石砌 9块扇面形石板构成第一环,向外每环依次
增加 9块.下一层的第一环比上一层的最后一环多 9块,向外每环依次也增加 9块.已知每
层环数相同,且下层比中层多 729块,则三层共有扇面形石板(不含天心石)( )
1/18
A.3699块 B.3474块 C.3402块 D.3339块
a
8.(2020 浙江)已知等差数列{an}的前 n项和 Sn ,公差 d 0,且 1 1.记 b1 S2 ,d
bn 1 S2n 2 S2n , n N *,下列等式不可能成立的是( )
A. 2a4 a2 a6 B. 2b4 b2 b6 C
2
.a4 a2a8 D b
2
. 4 b2b8
等比数列通项与前 n 项和求解
1.(2022全国乙卷文 10理 8)已知等比数列 an 的前 3项和为 168, a2 a5 42,则
a6 ( )
A. 14 B. 12 C. 6 D. 3
2.(2021 上海)已知{an}为无穷等比数列,a1 3,an 的各项和为 9,bn a2n,则数列{bn}
的各项和为__________.
3.(2021 文科甲卷)记 Sn为等比数列{an}的前 n项和.若 S2 4,S4 6,则 S6 ( )
A.7 B.8 C.9 D.10
4.(2020 江苏)设{an}是公差为 d 的等差数列,{bn}是公比为 q的等比数列.已知数列
{an bn}的前 n项和 Sn n
2 n 2n 1(n N*),则 d q的值是__________.
2/18
5.(2020新课标Ⅱ理)数列{an}中,a
15 5
1 2,am n aman .若ak 1 ak 2 ak 10 2 2 ,
则 k ( )
A.2 B.3 C.4 D.5
数列的单调性与最值
1. (2022北京)设 an 是公差不为 0的无穷等差数列,则“ an 为递增数列”是“存在正
整数 N0 ,当 n N0 时, an 0”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
2.(2022上海春考)已知等比数列{an}的前 n项和为 Sn,前 n项积为Tn ,则下列选项判断
正确的是( )
A.若 S2022 S2021 ,则数列{an}是递增数列
B.若T2022 T2021,则数列{an}是递增数列
C.若数列{Sn}是递增数列,则 a2022 a2021
D.若数列{Tn}是递增数列,则 a2022 a2021
3.(2021 甲卷)等比数列{an}的公比为 q,前 n项和为 Sn.设甲:q 0,乙:{Sn}是递
增数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
4.(2020北京)在等差数列{an}中,a1 9,a5 1.记Tn a1a2 an (n 1,2, ),
3/18
则数列{Tn} ( )
A.有最大项,有最小项 B.有最大项,无最小项
C.无最大项,有最小项 D.无最大项,无最小项
数列与实际生活情境结合
1. (2022新高考 II 1 )图 是中国古代建筑中的举架结构,AA ,BB ,CC ,DD 是桁,相邻
桁的水平距离称为步,垂直距离称为举,图 2是某古代建筑屋顶截面的示意图.其中
DD1,CC1,BB1, AA1是举,OD1,DC1,CB1 ,BA1是相等的步,相邻桁的举步之比分别为
DD1 0.5, CC1 k ,BB1 k , AA 1 1 k .已知 k ,k ,k 成公差为 0.1的等差数列,且直OD1 DC1 CB
2 BA 3 1 2 31 1
线OA的斜率为 0.725,则 k3 ( )
A. 0.75 B. 0.8 C. 0.85 D. 0.9
2. (2022全国乙卷理)嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国
第一颗环绕太阳飞行的人造行星,为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数
1
1 b 1 b 1 b 1 2 1
3
列 bn : 1 , 1 ,
1
1 ,1 …
,依此类推,其中
1 1 2 2 3
N k (k 1,2, ).则( )
4/18
A. b1 b5 B. b3 b8 C. b6 b2 D. b4 b7
3.(2021 北京)《中国共产党党旗党徽制作和使用的若干规定》指出,中国共产党党旗为旗
面缀有金黄色党徽图案的红旗,通用规格有五种.这五种规格党旗的长 a1, a2, a3, a4,
a5 (单位:cm)成等差数列,对应的宽为b1,b2,b3,b4,b5(单位:cm ),且长与宽
之比都相等.已知 a1 288, a5 96,b1 192,则b3 ( )
A.64 B.96 C.128 D.160
4.(2021 新高考Ⅰ)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴
把纸对折.规格为 20dm 12dm 的长方形纸,对折 1 次共可以得到 10dm 12dm,
20dm 6dm 两种规格的图形,它们的面积之和 S1 240dm
2
,对折 2 次共可以得到
5dm 12dm,10dm 6dm,20dm 3dm 2三种规格的图形,它们的面积之和 S2 180dm ,
以此类推.则对折 4次共可以得到不同规格图形的种数为__________;如果对折 n次,那么
n
Sk __________ dm2 .
k 1
数列与新定义
1.(2021 新高考Ⅱ 0 1)设正整数 n a0 2 a1 2 ak 1 2
k 1 a kk 2 ,其中 ai {0,1},
记 (n) a0 a1 ak ,则( )
A. (2n) (n) B. (2n 3) (n) 1
C. (8n 5) (4n 3) D n. (2 1) n
2.(2020 新课标Ⅱ理) 0 1周期序列在通信技术中有着重要应用.若序列 a1a2 an 满足
ai {0,1}(i 1,2, ),且存在正整数m,使得 ai m ai (i 1,2, )成立,则称其
为0 1周期序列,并称满足 ai m ai (i 1,2 )的最小正整数m为这个序列的周期.对于
5/18
m
周期为m的 0 1序列 a1a2 an ,C(k)
1
aiai k (k 1,2, ,m 1)是描述其m i 1
性质的重要指标,下列周期为 5的0 1序列中,满足C(k) 1 (k 1,2,3,4)的序列是( )
5
A.11010 B.11011 C.10001 D.11001
数列综合小题
1.(2022北京)己知数列 an 各项均为正数,其前 n项和 Sn满足 an Sn 9(n 1,2, ).给
出下列四个结论:
① an 的第 2项小于 3; ② an 为等比数列;
a a 1③ n 为递减数列; ④ n 中存在小于 的项.100
其中所有正确结论的序号是__________.
2.(2021 上海)已知 ai N *(i 1,2, ,9)对任意的 k N *(2 k 8),ak ak 1 1
或 ak ak 1 1中有且仅有一个成立,a1 6,a9 9,则 a1 a9 的最小值为__________.
6/18
近三年高考数学数列真题合集解析
等差数列通项与前 n 项和求解
1.【解答】由等差数列对称性可知:
S0 S5 0, S2 S3 , S1 S4,
其余各项均不相等,
Si (i 0,1,2 ,100)中不同的数值有:101 3 98个.
故答案为 98.
2.【解答】由 2S3 3S2 6可得 2 a1 a2+a3 3 a1 a2 6,
化简得 2 a1+2d 2a1 d 6,
解得 d 2.
故答案为 2.
3.【解答】因为等差数列{an}的首项为 3,公差为 2,
则 a10 a1 9d 3 9 2 21.
故答案为 21.
4.【解答】数列{an}是递增的整数数列,
n要取最大,后一个比前一个要大 1,
a1 3,
an n 2,
S (3 n 2)n 5n n
2
则 n ,2 2
试数取 n 11时, S11 88, a11 13,
7/18
100 S12 12 a11 13,
此时显然 n继续增大,则 a12 a11,不满足题意,
所以 n 11为最大值.
故选C.
5.【解答】数列{2n 1}与{3n 2}首项均为 1,此后每变大 6,即为二者公共项,
所以数列{an}是以 1为首项、以 6为公差的等差数列,
n(n 1)
故它的前 n项和为n 1 6 3n2 2n,
2
2
故答案为3n 2n.
6.【解答】根据题意,因为 a1 a10 a9 ,即 a1 a1 9d a1 8d ,
变形可得 a1 d,
9a 9 8da1 a2 a 1
9 2 9a1 36d 9d 36d 27所以 .
a10 a1 9d a1 9d d 9d 8
27
故答案为 .
8
7.【解答】设每一层有 n环,由题意可知,从内到外每环上扇面形石板数之间构成等差数列,
上层中心的首项为 a1 9,且公差 d 9,
由等差数列前 n项和的性质:
S 2n, S2n Sn , S3n S2n 成等差数列,且 (S3n S2n ) (S2n Sn ) n d,
n2所以 d 729,
则 n 9,
S S 27 9 27 26则三层共有扇面形石板 3n 27 9 3402块,2
故选C.
8.【解答】在等差数列{an}中, an a1 (n 1)d ,
8/18
a2 a1 d , a4 a1 3d, a8 a1 7d ,
而 2a4 a2 a6 ,根据等差数列的性质知 A正确,
bn 1 S2n 2 S2n,
b2 S4 S2 a3 a4 ,
b4 S8 S6 a7 a8 ,
b6 S12 S10 a11 a12 ,
所以对 2b4 b2 b6 ,即 2(a7 a8) a3 a4 a11 a12 (a3 a12 ) (a4 a11) ,
可知成立, B正确,
对C a2.若 4 a
2
2a8,则 (a1 3d) (a1 d)(a1 7d),
a2 6a d 9d 2 2即 1 1 a1 8a1d 7d
2 2
,得 a1d d ,
d a 0, a1 d ,符合 1 1,所以C正确;d
对D b2.若 4 b
2
2b8,则 (a7 a8) (a3 a4 )(a15 a16 ),
2
即 4a1 52a1d 169d
2 4a21 68a
2
1d 145d ,得16a1d 24d
2
,
d 0 2a a , 1 3d ,不符合 1 1,D错误;d
故选D.
等比数列通项与前 n 项和求解
1.【解答】设等比数列 an 的公比为 q,q 0,且显然 q 1,
a 1 q3 a 96
a1 a a
1 1
则 2 3
168
1 q ,解得 1 ,
q
a2 a5 a q a
4
1 1q 42 2
所以 a 5 .6 a1q 3
故选 D.
9/18
2.【解答】设{an}的公比为 q,
由 a1 3
3
, an 的各项和为 9,可得 9,1 q
q 2 2解得 ,所以 an 3 ( )
n 1
,
3 3
bn a2n 3 (
2)2n 1,
3
4
可得数列{bn}是首项为 2,公比为 的等比数列,9
{b } 2 18则数列 n 的各项和为 4 .1 5
9
18
故答案为 .
5
3.【解答】 Sn 为等比数列{an}的前 n项和, S2 4, S4 6,
由等比数列的性质,可知 S2, S4 S2 , S6 S4 成等比数列,
4,2, S6 6成等比数列,
22 4(S6 6),解得 S6 7.
故选 A.
4.【解答】依题意,数列{an}的通项公式 an a1 (n 1)d ,
d 2
所以其前 n项和 n (a d )n,
2 1 2
当{bn}中,当公比 q 1时,其前 n项和 nb1,
而{an b }
d 2 d 2 n
n 的前 n项和 Sn n (a1 )n nb1 n n 2 1(n N*),显然没有出2 2
现 2n,所以 q 1,
n
{b } b (q 1) b q
n b
则 n 的前 n项和为 1 1 1 ,q 1 q 1 q 1
S d n2 (a d
n
所以 n 1 )n
b
1
q b
1 n2 n 2 n 1(n N*) ,
2 2 q 1 q 1
10/18
d
1
2
a
d
1 1
由两边对应项相等可得: 2 解得: d 2, a1 0,q 2,b1 1,
q 2
b1 1
q 1
所以 d q 4,
故答案为 4
5.【解答】由 a1 2,且 am n aman ,
取m 1,得 an 1 a1an 2an ,
a
n 1 2,
an
则数列{an}是以 2为首项,以 2为公比的等比数列,
a 2 2k 2k 1则 k 1 ,
2k 1 10
ak 1 ak 2 a
(1 2 )
211 k 2k 1 215 5k 10 2 ,1 2
k 1 5,即 k 4.
故选C.
数列的单调性与最值
1.【解答】设等差数列 an 的公差为 d ,则 d 0,记 x 为不超过 x的最大整数.
若 an 为单调递增数列,则 d 0,
若 a1 0,则当 n 2时, an a1 0;若 a1 0,则 an a1 n 1 d,
a a a1 a 由 n 11 n 1 d 0可得 n 1 ,取 N0 1 1,则当 n N0 时, ad d n
0,
11/18
所以,“ an 是递增数列” “存在正整数 N0 ,当 n N0 时, an 0 ”;
若存在正整数 N0 ,当 n N0 时, an 0,取 k N 且 k N0, ak 0,
假设 d 0,令 a a n k d 0 a a可得 n k k ,且 k kn k k ,d d
a
当 n k
k
1时, an 0,与题设矛盾,假设不成立,则 d 0,即数列 an 是递增 d
数列.
所以,“ an 是递增数列” “存在正整数 N0 ,当 n N0 时, an 0 ”.
所以,“ an 是递增数列”是“存在正整数N0 ,当 n N0 时, an 0 ”的充分必要条件.
故选 C.
2.【解答】如果数列 a1 1,公比为 2,满足 S2022 S2021 ,但是数列{an}不是递增数列,
所以 A不正确;
1
如果数列 a1 1,公比为 ,满足T2 2022
T2021 ,但是数列{an}不是递增数列,所以 B不
正确;
1 1 ( ) n1 1
如果数列 a1 1,公比为 , S 2n 1 2(1 n ),数列{Sn}是递增数列,但是2 2
2
a2022 a2021,所以C不正确;
数列{Tn}是递增数列,可知Tn Tn 1,可得 an 1,所以 q 1,可得 a2022 a2021正确,所
以D正确;
故选D.
3.【解答】若 a1 1,q 1,则 Sn na1 n,则{Sn}是递减数列,不满足充分性;
S a1 nn (1 q ),1 q
S a1 n 1则 n 1 (1 q ),1 q
12/18
S S a 1 (q nn 1 n q
n 1) a n
1 q 1
q ,
若{Sn}是递增数列,
Sn 1 Sn a
n
1q 0,
则 a1 0, q 0,
满足必要性,
故甲是乙的必要条件但不是充分条件,
故选 B.
a a 1 ( 9)
4.【解答】设等差数列{an}的公差为 d ,由 a 5 11 9,a5 1,得d 2,5 1 4
an 9 2(n 1) 2n 11.
由 an 2n 11
11
0,得 n ,而 n N *,
2
可知数列{an}是单调递增数列,且前 5项为负值,自第 6项开始为正值.
可知T1 9 0,T2 63 0,T3 315 0,T4 945 0为最大项,
自T5起均小于 0,且逐渐减小.
数列{Tn}有最大项,无最小项.
故选 B.
数列与实际生活情境结合
1.【解答】设OD1 DC1 CB1 BA1 1,则CC1 k1,BB1 k2 ,AA1 k3 ,
DD CC BB AA
依题意,有 k3 0.2 k1,k3 0.1 k2 ,且
1 1 1 1 0.725,
OD1 DC1 CB1 BA1
0.5 3k3 0.3所以 0.725,故 k3 0.9,4
故选 D
13/18
2.【解答】因为 N*k k 1,2, ,
1
1 1
所以 1 1 ,
1 ,得到
1 b1 b2
,
2 1 2
11
1
同理 1 1 ,可得b2 b3 ,2 b1 b32 3
1 1
1 ,
1 1
1
1 1 1
又因为 2 2 2 2 ,
1 133 34 4
故b2 b4,b3 b4;
以此类推,可得b1 b3 b5 b7 …,b7 b8,故 A错误;
b1 b7 b8,故 B错误;
1 1
2 12 ,得b2 b6,故 C错误;
13 … 6
1 11 1
12
1
2 … ,得 ,故 正确.
1 1
b4 b7 D
3 6 4 7
故选 D.
3.【解答】{an}和{b }
a
n 是两个等差数列,且
k (1 k 5)是常值,由于 a1 288,a5 96,bk
a
故 a 1 a53 192,2
a3 a1 288 3由于
b3 b1 192 2
所以b3 128.
14/18
a1 a5 b a b另 ,解得: 5 1 64
b1 b
5
5 a1
故:b b1 b3 5 128.2
故选C.
20dm 3 dm,10dm 3 dm,5dm 3dm, 5 dm 6dm 54.【解答】易知有 , dm 12dm,共
4 2 2 4
5种规格;
k k 1 240 S 240(k 1)由题可知,对折 次共有 种规格,且面积为
2k
,故 k ,2k
n n k 1 n S k 1 1
n k 1
则 k 240 ,记T 2k n 2k ,则 T ,k 1 k 1 k 1 2 n k 1 2k 1
1 nT k 1
n
k 1
n 1 k 2 n 1 k 1 n 1
n 2 2k
2k 1
1 ( k 1 k 1 ) 2 n 1k 1 k 1 k 1 k 1 2 2
1 (1 1 n 1 )
1 n 1 3 n 3 4 21 n 1 ,1 2 2 2
n 1
2
n 3
Tn 3 2n
,
n
Sk 240(3 n 3 n ).
k 1 2
故答案为 5; 240(3 n 3 ).
2n
数列与新定义
1 1 2 k.【解答】 2n a0 2 a1 2 ak 1 2 ak 2
k 1
,
(2n) (n) a0 a1 ak , A对;
当 n 2 0时,2n 3 7 1 2 1 21 1 22, (7) 3 0 1. 2 0 2 1 2 , (2)
0 1 1, (7) (2) 1, B错;
15/18
8n 5 a0 2
3 a1 2
4 a 2k 3k 5 1 2
0 1 22 a 230 a1 2
4 ak 2
k 3
,
(8n 5) a0 a1 a k 2 ,
4n 3 a 22 a 23 a 2k 2 3 1 20 1 21 a 22 a 23 a 2k 20 1 k 0 1 k
(4n 3) a0 a1 a k 2 (8n 5) . C 对;
2n 1 1 20 1 21 1 2n 1, (2n 1) n, D对.
故选 ACD.
2.【解答】对于 A选项:序列 11010 11010
C 1
5 1
(1) aiai 1 (1 0 0 0 0) 1 ,5 i 1 5 5
5
C 1 1(2) aiai 2 (0 1 0 1 0) 2 1 1 ,不满足C(k) (k 1,2,3, 4),5 i 1 5 5 5 5
故排除 A;
对于 B选项:序列 11011 11011
1 5C 1(1) a a (1 0 0 1 1) 3 1 ,不满足条件,排除;
5 i i 1i 1 5 5 5
对于C选项:序列 10001 10001 10001
1 5C(1) a a 1 1
5 i i 1 (0 0 0 0 1) ,i 1 5 5
C 1
5
(2) a 1iai 2 (0 0 0 0 0) 0,5 i 1 5
1 5C a a 1(3) i i 3 (0 0 0 0 0) 0,5 i 1 5
5
C 1 1 1(4) aiai 4 (1 0 0 0 0) ,符合条件,5 i 1 5 5
对于D选项:序列 11001 11001
16/18
1 5C a a 1 (1 2 1(1) i i 1 0 0 0 1) 不满足条件.5 i 1 5 5 5
故选C.
数列综合小题
1.【解答】由题意可知, n N , an 0,
当 n 1时, a2 9,可得 a1 3;1
9
当 n 2时,由 Sn 可得 S
9 9 9
a n 1
,两式作差可得 a
a n
,
n n 1 an an 1
9 9 9
所以, an,则 a2 3,整理可得a22 3a2 9 0,an 1 an a2
因为 a 0,解得a 3 5 32 3,①对;2 2
2
假设数列 an 为等比数列,设其公比为 q,则 a2 ,即
9 81 ,
2 a1a3 S
2 S1S3
所以, S 22 S S ,可得 a
2 1 q 2 a2 1 q q2 ,解得q 0,不合乎题意,1 3 1 1
故数列 an 不是等比数列,②错;
9 9 9 a a
当 n 2时,a n 1 n
n 0,可得 a a ,所以,数列 a 为递减数an a n n 1 nn 1 anan 1
列,③对;
1 1
假设对任意的 n N ,a ,则n S100000 100000 1000,100 100
9 9 1
所以, a100000 ,与假设矛盾,假设不成立,④对.S100000 1000 100
故答案为①③④.
2.【解答】设bk ak 1 ak ,由题意可得,bk ,bk 1恰有一个为 1,
17/18
如果b1 b3 b5 b7 b9 1,那么 a1 6, a2 7, a3 1, a4 a3 1 2,
同样也有, a5 1, a6 a5 1 2, a7 1, a8 a7 1 2,
全部加起来至少是6 7 1 2 1 2 1 2 9 31;
如果b2 b4 b6 b8 1,那么 a8 8, a2 1, a3 a2 1 2,
同样也有, a4 1, a5 2, a6 1, a7 2,
全部加起来至少是6 1 2 1 2 1 2 8 9 32,
综上所述,最小应该是 31.
故答案为 31.
18/18
同课章节目录
