第25章圆综合测试卷及答案
图片预览



文档简介
第25章 综合质量检测试卷
(温馨提示:考试时间:90分钟 总分120分)
一、精心选一选(每小题3分,共30分)
1.如图1,AB是⊙O的直径,点C在⊙O上,若∠A=40 ,则∠B的度数为
( )
A.80 B.60 C.50 D.40
2.如图2,在⊙O中,弦∥,若,则( )
A. B. C. D.
3.如图3所示,实线部分是半径为9m的两个圆相交所成的游泳池,每条虚线弧所在的圆都经过另一个圆的圆心,则游泳池的周长为 ( )
A. B. C. D.
4.如图4,AB是⊙O的弦,BC与⊙O相切于点B,连结OA 、OB.若∠ABC=70°,则∠A等于 ( )
A.15° B.20° C.30° D.70°
5.如图5所示,⊙O的直径为10,圆心O到弦AB的距离OM的长是3,则弦AB的长是( )
A.4 B.6 C.7 D.8
6.如图6所示,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C两点,则BC等于 ( )
A. B. C. D.
7.如图7,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为 ( )
A.10π B. C.π D.π
8.已知两圆的半径分别为1和3,当这两圆内含时,圆心距d的范围是( )
A. B. C. D.
9.如图8所示,AE切⊙O于点E,AC=CO=)B=10,则线段AE的长为 ( )
A. B.15 C. D.20
10.如图9是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是 ( )
A. B.
C. D.
二、耐心填一填(每小题3分,共30分)
11.如图10所示,点D在以AC为直径的⊙O上,如果,那么=
.
12.如图11所示,已知⊙O的半径为5,弦AB=8,P是弦AB上任意一点,则OP的取值范围是 .
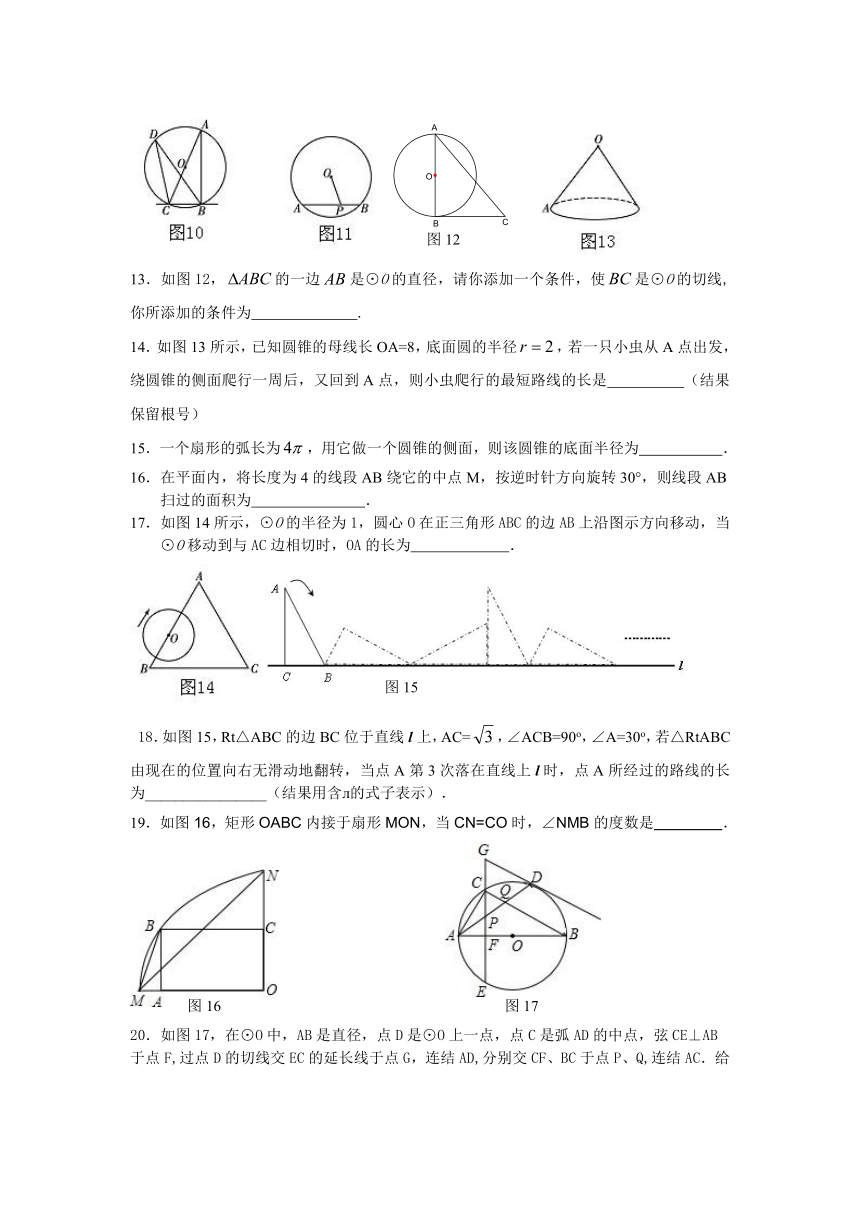
13.如图12,的一边是⊙O的直径,请你添加一个条件,使是⊙O的切线,你所添加的条件为 .
14.如图13所示,已知圆锥的母线长OA=8,底面圆的半径,若一只小虫从A点出发,绕圆锥的侧面爬行一周后,又回到A点,则小虫爬行的最短路线的长是 (结果保留根号)
15.一个扇形的弧长为,用它做一个圆锥的侧面,则该圆锥的底面半径为 .
16.在平面内,将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°,则线段AB扫过的面积为 .
17.如图14所示,⊙O的半径为1,圆心O在正三角形ABC的边AB上沿图示方向移动,当⊙O移动到与AC边相切时,OA的长为 .
18.如图15,Rt△ABC的边BC位于直线l上,AC=,∠ACB=90o,∠A=30o,若△RtABC由现在的位置向右无滑动地翻转,当点A第3次落在直线上l时,点A所经过的路线的长为________________(结果用含л的式子表示).
19.如图16,矩形OABC内接于扇形MON,当CN=CO时,∠NMB的度数是 .
20.如图17,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连结AD,分别交CF、BC于点P、Q,连结AC.给出下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AP·AD=CQ·CB.其中正确的是 (写出所有正确结论的序号).
三、认真想一想(共60分)
21.(10分)如图19,在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.
.
22.(12分)如图20,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
23.(12分)如图21所示,已知⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,CB的延长线交⊙O1于D,E为AB延长线上一点,连接DE,AD.
(1)试说明AD是⊙O1的直径;
(2)若,试说明DE是⊙O1的切线.
24.(12分)当汽车在雨天行驶时,为了看清楚道路,司机要启动前方挡风玻璃上的雨刷器.如图是某汽车的一个雨刷器的示意图,雨刷器杆AB与雨刷CD在B处固定连接(不能转动),当杆AB绕A点转动90°时,雨刷CD扫过的面积是多少呢?小明仔细观察了雨刷器的转动情况,量得CD=80cm、∠DBA=20°,端点C、D与点A的距离分别为115cm、35cm.他经过认真思考只选用了其中的部分数据就求得了结果,你知道小明是怎样计算的吗?也请你算一算雨刷CD扫过的面积是多少?(π取3.14).
25. (14分)如图23,在△ABC中,BE是它的角平分线,∠C=900,D在AB边上,以DB为直径的半圆O经过点E交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA=,⊙O的半径为4,求图中阴影部分的面积.
一、选择题
1.C
2.D
3.D[提示:连接两圆圆心及其中一个交点,得到一个等边三角形,可得虚线部分弧所对圆心角为,则游泳池周长为]
4.B
5.D[提示:∵,∴.∵OM=3,∴AM=4,AB=2AM=8]
6.A[提示:∵△ABO为正三角形,BC⊥AO,∴]
7.C [顶点A经过的路径是以C为圆心AC为半径,圆心角为60°的弧]
8.D
9.C[提示:∵AE是⊙O的切线,,又AC=CO=EO=10,∴AE=]
10.C[提示:连接OD,,∠DOC=60°,S阴影=S扇形AOD﹣S△DOC]
二、填空题
11.[提示:,]
12.[提示:O到AB的距离为3,当P为AB中点时,OP最小为3;当P与A(或B)重合时最大为5]
13.BC⊥AB或∠ABC=900
14.
15.2
16.
17.
18.+ [提示:可以分别求出每次的旋转角与旋转半径]
19.[提示:连接OB,∠BOC=60°,∠NMB=∠BOC]
20.②③④
21.∵AB⊙O是直径 , ∴BD ⊥AD.
又∵CF⊥AD,∴BD∥CF .∴∠BDC=∠C .
又∵∠BDC=∠BOC,∴∠C=∠BOC.
∵AB⊥CD,∴∠C=30°.∴∠ADC=60°.
22.(1)线段AC是⊙O的切线;
理由如下:∵∠CAD=∠CDA(已知),∠BDO=∠CDA,
∴∠BDO=∠CAD.
又∵OA=OB,∴∠B=∠OAB.
∵OB⊥OC(已知),∴∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°.
∴线段AC是⊙O的切线.
(2)设AC=.∵∠CAD=∠CDA,
∴DC=AC=.∵OA=5,OD=1,∴OC=OD+DC=1+.
∵由(1)知,AC是⊙O的切线,
∴在Rt△OAC中,根据勾股定理得,OC2=AC2+OA2,即
解得=12,即AC=12.
23.(1)证;(2)证
24.
25.(1)连接OE,∵OB=OE∴∠OBE=∠OEB.∵BE是△ABC角平分线,∴∠OBE=∠EBC,∴∠OEB=∠EBC, ∴OE∥BC,∵∠C=900,∴∠AEO=∠C=900,∴AC是⊙O切线.
(2)连接OF.∵sinA= ,∴∠A=30°. ∵⊙O的半径为4,∴AO=2OE=8,
∴AE=4 ,∠AOE=60°,∴AB=12,∴BC= AB=6 AC=6 ,∴CE=AC-AE=2 .
∵OB=OF,∠ABC=60°,∴△OBF是正三角形.∴∠FOB=60°,CF=6-4=2,∴∠EOF=60°.
∴S梯形OECF= (2+4)×2 =6 . S扇形EOF=60π×42 ÷360 = π.
∴S阴影部分=S梯形OECF-S扇形EOF=6-π.
图1
图2
图4
图7
图9
图12
图15
图16
图17
图19
图20
图23
(温馨提示:考试时间:90分钟 总分120分)
一、精心选一选(每小题3分,共30分)
1.如图1,AB是⊙O的直径,点C在⊙O上,若∠A=40 ,则∠B的度数为
( )
A.80 B.60 C.50 D.40
2.如图2,在⊙O中,弦∥,若,则( )
A. B. C. D.
3.如图3所示,实线部分是半径为9m的两个圆相交所成的游泳池,每条虚线弧所在的圆都经过另一个圆的圆心,则游泳池的周长为 ( )
A. B. C. D.
4.如图4,AB是⊙O的弦,BC与⊙O相切于点B,连结OA 、OB.若∠ABC=70°,则∠A等于 ( )
A.15° B.20° C.30° D.70°
5.如图5所示,⊙O的直径为10,圆心O到弦AB的距离OM的长是3,则弦AB的长是( )
A.4 B.6 C.7 D.8
6.如图6所示,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C两点,则BC等于 ( )
A. B. C. D.
7.如图7,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为 ( )
A.10π B. C.π D.π
8.已知两圆的半径分别为1和3,当这两圆内含时,圆心距d的范围是( )
A. B. C. D.
9.如图8所示,AE切⊙O于点E,AC=CO=)B=10,则线段AE的长为 ( )
A. B.15 C. D.20
10.如图9是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是 ( )
A. B.
C. D.
二、耐心填一填(每小题3分,共30分)
11.如图10所示,点D在以AC为直径的⊙O上,如果,那么=
.
12.如图11所示,已知⊙O的半径为5,弦AB=8,P是弦AB上任意一点,则OP的取值范围是 .
13.如图12,的一边是⊙O的直径,请你添加一个条件,使是⊙O的切线,你所添加的条件为 .
14.如图13所示,已知圆锥的母线长OA=8,底面圆的半径,若一只小虫从A点出发,绕圆锥的侧面爬行一周后,又回到A点,则小虫爬行的最短路线的长是 (结果保留根号)
15.一个扇形的弧长为,用它做一个圆锥的侧面,则该圆锥的底面半径为 .
16.在平面内,将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°,则线段AB扫过的面积为 .
17.如图14所示,⊙O的半径为1,圆心O在正三角形ABC的边AB上沿图示方向移动,当⊙O移动到与AC边相切时,OA的长为 .
18.如图15,Rt△ABC的边BC位于直线l上,AC=,∠ACB=90o,∠A=30o,若△RtABC由现在的位置向右无滑动地翻转,当点A第3次落在直线上l时,点A所经过的路线的长为________________(结果用含л的式子表示).
19.如图16,矩形OABC内接于扇形MON,当CN=CO时,∠NMB的度数是 .
20.如图17,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连结AD,分别交CF、BC于点P、Q,连结AC.给出下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AP·AD=CQ·CB.其中正确的是 (写出所有正确结论的序号).
三、认真想一想(共60分)
21.(10分)如图19,在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.
.
22.(12分)如图20,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
23.(12分)如图21所示,已知⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,CB的延长线交⊙O1于D,E为AB延长线上一点,连接DE,AD.
(1)试说明AD是⊙O1的直径;
(2)若,试说明DE是⊙O1的切线.
24.(12分)当汽车在雨天行驶时,为了看清楚道路,司机要启动前方挡风玻璃上的雨刷器.如图是某汽车的一个雨刷器的示意图,雨刷器杆AB与雨刷CD在B处固定连接(不能转动),当杆AB绕A点转动90°时,雨刷CD扫过的面积是多少呢?小明仔细观察了雨刷器的转动情况,量得CD=80cm、∠DBA=20°,端点C、D与点A的距离分别为115cm、35cm.他经过认真思考只选用了其中的部分数据就求得了结果,你知道小明是怎样计算的吗?也请你算一算雨刷CD扫过的面积是多少?(π取3.14).
25. (14分)如图23,在△ABC中,BE是它的角平分线,∠C=900,D在AB边上,以DB为直径的半圆O经过点E交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA=,⊙O的半径为4,求图中阴影部分的面积.
一、选择题
1.C
2.D
3.D[提示:连接两圆圆心及其中一个交点,得到一个等边三角形,可得虚线部分弧所对圆心角为,则游泳池周长为]
4.B
5.D[提示:∵,∴.∵OM=3,∴AM=4,AB=2AM=8]
6.A[提示:∵△ABO为正三角形,BC⊥AO,∴]
7.C [顶点A经过的路径是以C为圆心AC为半径,圆心角为60°的弧]
8.D
9.C[提示:∵AE是⊙O的切线,,又AC=CO=EO=10,∴AE=]
10.C[提示:连接OD,,∠DOC=60°,S阴影=S扇形AOD﹣S△DOC]
二、填空题
11.[提示:,]
12.[提示:O到AB的距离为3,当P为AB中点时,OP最小为3;当P与A(或B)重合时最大为5]
13.BC⊥AB或∠ABC=900
14.
15.2
16.
17.
18.+ [提示:可以分别求出每次的旋转角与旋转半径]
19.[提示:连接OB,∠BOC=60°,∠NMB=∠BOC]
20.②③④
21.∵AB⊙O是直径 , ∴BD ⊥AD.
又∵CF⊥AD,∴BD∥CF .∴∠BDC=∠C .
又∵∠BDC=∠BOC,∴∠C=∠BOC.
∵AB⊥CD,∴∠C=30°.∴∠ADC=60°.
22.(1)线段AC是⊙O的切线;
理由如下:∵∠CAD=∠CDA(已知),∠BDO=∠CDA,
∴∠BDO=∠CAD.
又∵OA=OB,∴∠B=∠OAB.
∵OB⊥OC(已知),∴∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°.
∴线段AC是⊙O的切线.
(2)设AC=.∵∠CAD=∠CDA,
∴DC=AC=.∵OA=5,OD=1,∴OC=OD+DC=1+.
∵由(1)知,AC是⊙O的切线,
∴在Rt△OAC中,根据勾股定理得,OC2=AC2+OA2,即
解得=12,即AC=12.
23.(1)证;(2)证
24.
25.(1)连接OE,∵OB=OE∴∠OBE=∠OEB.∵BE是△ABC角平分线,∴∠OBE=∠EBC,∴∠OEB=∠EBC, ∴OE∥BC,∵∠C=900,∴∠AEO=∠C=900,∴AC是⊙O切线.
(2)连接OF.∵sinA= ,∴∠A=30°. ∵⊙O的半径为4,∴AO=2OE=8,
∴AE=4 ,∠AOE=60°,∴AB=12,∴BC= AB=6 AC=6 ,∴CE=AC-AE=2 .
∵OB=OF,∠ABC=60°,∴△OBF是正三角形.∴∠FOB=60°,CF=6-4=2,∴∠EOF=60°.
∴S梯形OECF= (2+4)×2 =6 . S扇形EOF=60π×42 ÷360 = π.
∴S阴影部分=S梯形OECF-S扇形EOF=6-π.
图1
图2
图4
图7
图9
图12
图15
图16
图17
图19
图20
图23
