1.4 解直角三角形 课件(共15张PPT)
文档属性
| 名称 | 1.4 解直角三角形 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 794.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 13:38:32 | ||
图片预览




文档简介
(共15张PPT)
第一章 直角三角形的边角关系
北师大版九年级数学下册
1.4 解直角三角形
学习&目标
1.掌握解直角三角形的概念;(重点)
2.掌握解直角三角形的依据并能熟练解题.(重点、难点)
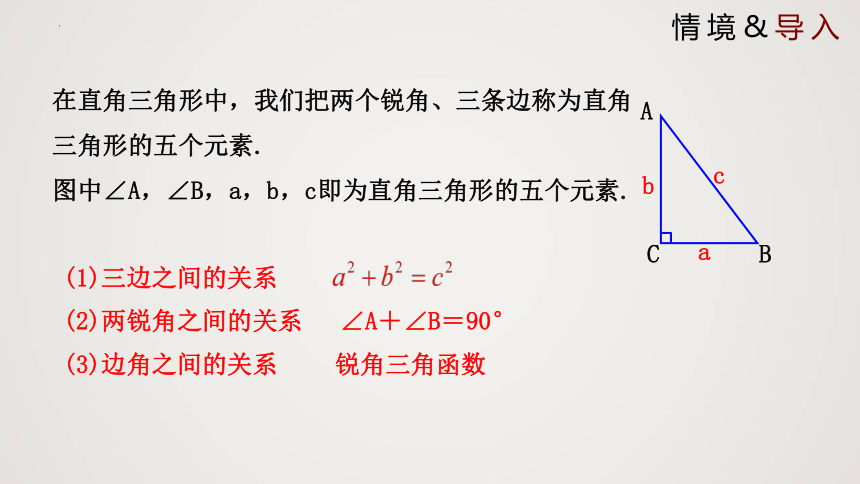
情境&导入
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
锐角三角函数
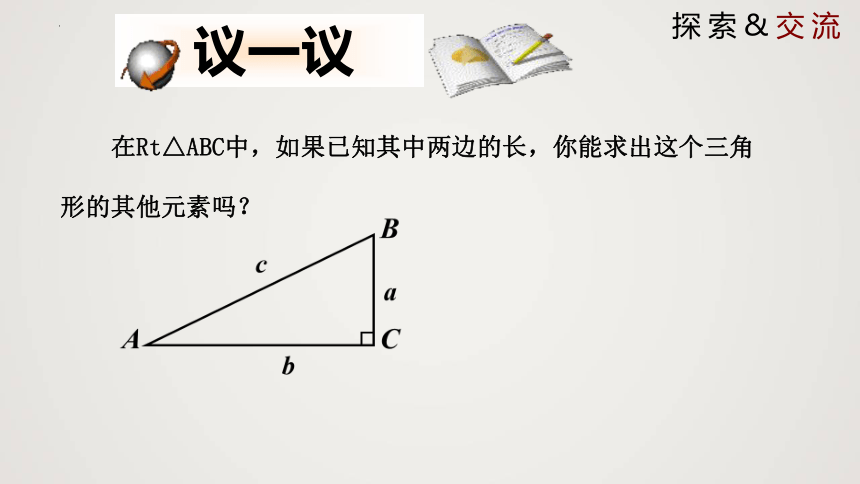
在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
议一议
探索&交流
例题&解析
例题欣赏
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为 a,b ,c,且a= ,b= ,求这个三角形的其他元素.
解:Rt△ABC中,a2+b2=c2,a= ,b= ,
∴sinB= ,
则∠B=30°,∠A=60°.
∴c= .
A
C
B
a
c
b
A
B
a
b
c
C
解直角三角形:在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
探索&交流
探索&交流
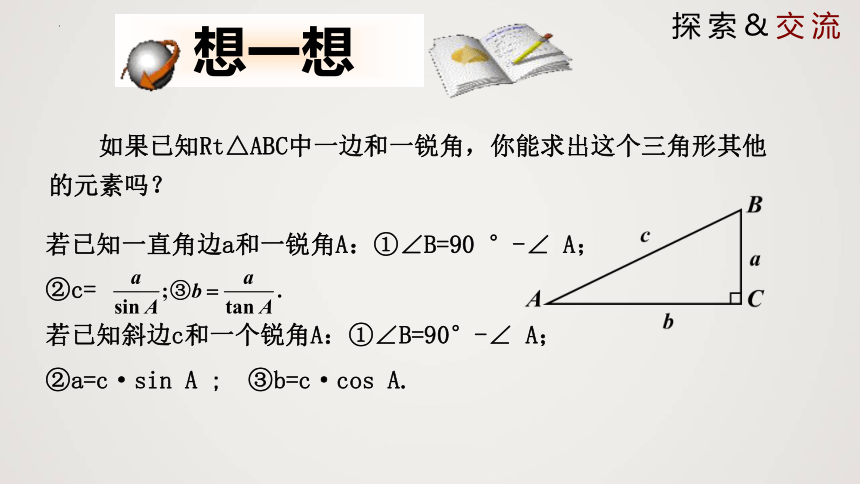
想一想
如果已知Rt△ABC中一边和一锐角,你能求出这个三角形其他的元素吗?
若已知一直角边a和一锐角A:①∠B=90 °-∠ A;
②c=
若已知斜边c和一个锐角A:①∠B=90°-∠ A;
②a=c·sin A ; ③b=c·cos A.
例题&解析
例题欣赏
例2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为 a,b,c,且b=30,∠B=25°,求这个三角形的其他元素(边长精确到1).
解:Rt△ABC中,∠C=90 ° ,∠B=25°,
∵sinB= ,b=30,
∴c= .
∵tanB= ,b=30,
∴a= .
A
C
B
a
c
b
∴∠A=65 °.
探索&交流
两角
不能
两边
一角一边
在Rt△ABC中,如果已知∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?
探索&交流
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
例题&解析
例题欣赏
例3.如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.
D
A
B
C
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +
练习&巩固
1.在Rt△ABC中,∠C=90°,AB=2 ,AC= ,则∠A的度数为( )
A.90° B.60°
C.45° D.30°
练习&巩固
2.在△ABC中,∠C=90°,若∠B=2∠A,b=3,则a等于( )
A. B.
C.6 D.
练习&巩固
3.如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB= ,则AC的长为( )
A.3 B.3.75
C.4.8 D.5
小结&反思
在直角三角形中有三条边、三个角,它们具备以下关系:
(1)三边之间关系:a2+b2=c2 (勾股定理).
(2)锐角之间的关系:∠A+ ∠B = 90°.
(3)边角之间的关系:
第一章 直角三角形的边角关系
北师大版九年级数学下册
1.4 解直角三角形
学习&目标
1.掌握解直角三角形的概念;(重点)
2.掌握解直角三角形的依据并能熟练解题.(重点、难点)
情境&导入
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.
图中∠A,∠B,a,b,c即为直角三角形的五个元素.
锐角三角函数
在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
议一议
探索&交流
例题&解析
例题欣赏
例1.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为 a,b ,c,且a= ,b= ,求这个三角形的其他元素.
解:Rt△ABC中,a2+b2=c2,a= ,b= ,
∴sinB= ,
则∠B=30°,∠A=60°.
∴c= .
A
C
B
a
c
b
A
B
a
b
c
C
解直角三角形:在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
探索&交流
探索&交流
想一想
如果已知Rt△ABC中一边和一锐角,你能求出这个三角形其他的元素吗?
若已知一直角边a和一锐角A:①∠B=90 °-∠ A;
②c=
若已知斜边c和一个锐角A:①∠B=90°-∠ A;
②a=c·sin A ; ③b=c·cos A.
例题&解析
例题欣赏
例2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为 a,b,c,且b=30,∠B=25°,求这个三角形的其他元素(边长精确到1).
解:Rt△ABC中,∠C=90 ° ,∠B=25°,
∵sinB= ,b=30,
∴c= .
∵tanB= ,b=30,
∴a= .
A
C
B
a
c
b
∴∠A=65 °.
探索&交流
两角
不能
两边
一角一边
在Rt△ABC中,如果已知∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?
探索&交流
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
例题&解析
例题欣赏
例3.如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.
D
A
B
C
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +
练习&巩固
1.在Rt△ABC中,∠C=90°,AB=2 ,AC= ,则∠A的度数为( )
A.90° B.60°
C.45° D.30°
练习&巩固
2.在△ABC中,∠C=90°,若∠B=2∠A,b=3,则a等于( )
A. B.
C.6 D.
练习&巩固
3.如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB= ,则AC的长为( )
A.3 B.3.75
C.4.8 D.5
小结&反思
在直角三角形中有三条边、三个角,它们具备以下关系:
(1)三边之间关系:a2+b2=c2 (勾股定理).
(2)锐角之间的关系:∠A+ ∠B = 90°.
(3)边角之间的关系:
