第二十六章 反比例函数章末复习 课件(共28张PPT)
文档属性
| 名称 | 第二十六章 反比例函数章末复习 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 18:44:00 | ||
图片预览






文档简介
(共28张PPT)
反比例函数
章节总结
第二十六章
学习目标
通过探索实际问题数量关系的过程,理解反比例函数的概念。能画出反比例函数的图象,并根据图象和解析式掌握反比例函数的主要性质,体会反比例函数在实际生活中的应用。
重点
理解反比例函数的概念和性质。
难点
理解反比例函数系数的几何意义。
反比例函数是继二次函数后又一种比较重要的函数,并且对图像的把握要求更高,我们经常会通过数形结合的方法来解决相关的题。我们要全面了解反比例函数的相关概念及性质,与一次函数对比学习,它们既有联系又有区别,其难度相对于二次函数来说是比较简单的。
基础巩固(反比例函数的定义)
一般地,形如 y = (k 为常数,且 k ≠ 0)的函数,叫做反比例函数,其中 x 是自变量,y 是函数。
【注意】1)自变量 x 的取值范围是不等于 0 的一切实数.(x=0,分式 无意义)
2)反比例函数也写成y=kx-1或k=xy的形式。
基础巩固(反比例函数的图象与性质)
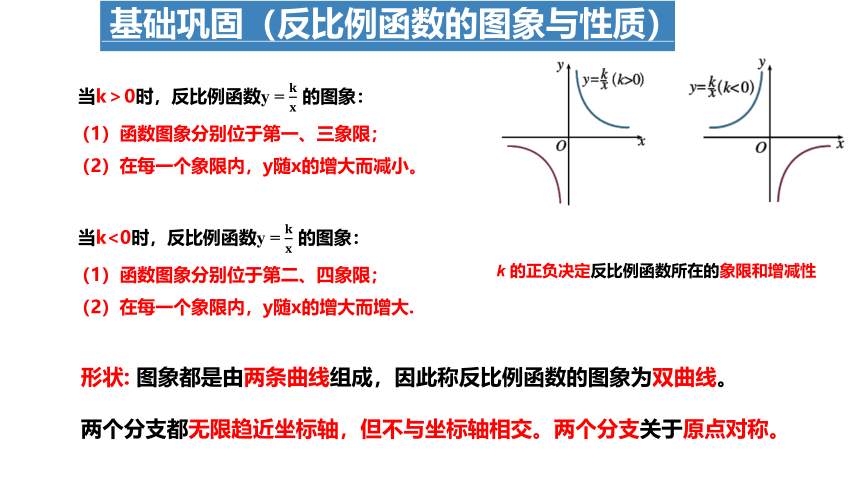
当k>0时,反比例函数y = 的图象:
(1)函数图象分别位于第一、三象限;
(2)在每一个象限内,y随x的增大而减小。
当k<0时,反比例函数y = 的图象:
(1)函数图象分别位于第二、四象限;
(2)在每一个象限内,y随x的增大而增大.
形状: 图象都是由两条曲线组成,因此称反比例函数的图象为双曲线。
两个分支都无限趋近坐标轴,但不与坐标轴相交。两个分支关于原点对称。
k 的正负决定反比例函数所在的象限和增减性
基础巩固(反比例函数k的几何意义)
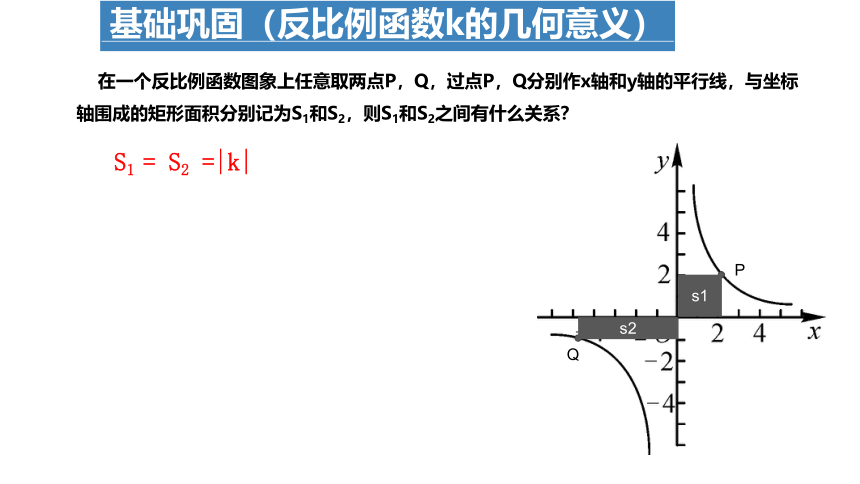
在一个反比例函数图象上任意取两点P,Q,过点P,Q分别作x轴和y轴的平行线,与坐标轴围成的矩形面积分别记为S1和S2,则S1和S2之间有什么关系?
s1
s2
P
Q
S1 = S2 =|k|
基础巩固(反比例函数k的几何意义)
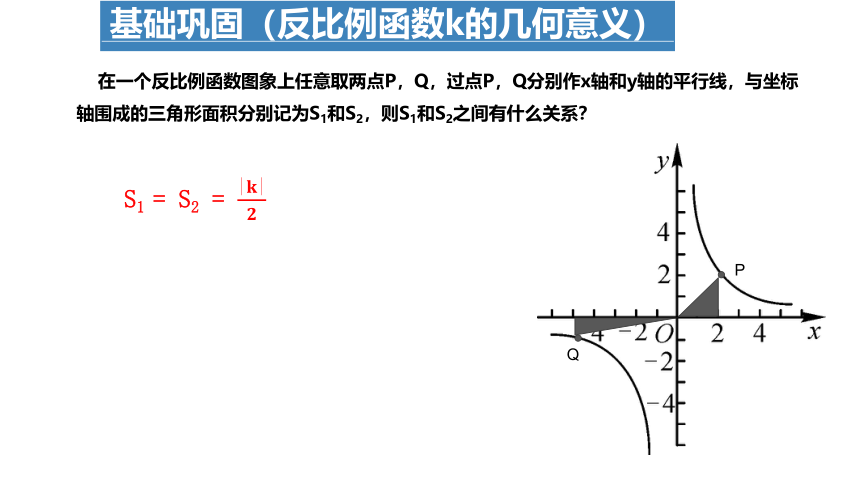
在一个反比例函数图象上任意取两点P,Q,过点P,Q分别作x轴和y轴的平行线,与坐标轴围成的三角形面积分别记为S1和S2,则S1和S2之间有什么关系?
P
Q
S1 = S2 =
在初中数学函数中,反比例函数作为一种特殊的函数,区别于一次函数和二次函数,它的函数图像是两个断开的分支,永远不与坐标轴相交。于是关于反比例函数的题目除了一些围绕其函数性质,求k的值等题目之外,就是与几何图形联系起来出题,这类题难度较高,常作为压轴题出现。
题型一(判断反比例函数)
1. 下列关系式中,y是x的反比例函数的是 ( )
A. B. C. D.
2. 下列函数:①y=2x,②y=,③y=x﹣1,④y=.其中,是反比例函数的有( )
A.0个 B.1个 C.2个 D.3个
题型二(根据反比例函数的定义求参数)
1. 已知是关于的反比例函数,则( )
A. B. C. D.为一切实数
2. 若函数y=(m﹣1)x|m|﹣2是反比例函数,则m的值是( )
A.m=﹣1 B.m=1
C.m=﹣1或m=1 D.m=﹣2或m=2
【详解】解:由题意得:,解得m=-1,故选:A.
题型三(反比例函数的图象与性质)
1. 下列反比例函数图象一定在第一、三象限的是( )
A. B. C. D.
2. 若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
3.已知函数是反比例函数,则此反比例函数的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、四象限 D.第二、三象限
题型三(反比例函数的图象与性质)
4.在反比例函数的图象的每一个分支上,y都随x的增大而减小,则k的取值范围是( )
A.k>1 B.k>0 C.k≥1 D.k<1
5.已知反比例函数(k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx﹣k的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
题型四(反比例系数k的几何意义)
1 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A.3 B.﹣3 C.6 D.﹣6
【详解】连结OA,如图,
∵AB⊥x轴,∴OC∥AB,
∴S△OAB=S△CAB=3,而S△OAB=|k|,∴|k|=3,
∵k<0,∴k=﹣6.故选D.
题型四(反比例系数k的几何意义)
2 如图,在平面直角坐标系中,函数 y kx 与 y 的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
A.2 B.4 C.6 D.8
【详解】
连接OC,设AC⊥y轴交y轴为点D,
∵反比例函数y=-为对称图形,∴O为AB 的中点,∴S△AOC=S△COB,
∵由题意得A点在y=-上,B点在y=上,∴S△AOD=×OD×AD=xy=1;
S△COD=×OC×OD=xy=2;
S△AOC= S△AOD+ S△COD=3,
∴S△ABC= S△AOC+S△COB=6.故答案选C.
题型四(反比例系数k的几何意义)
3. 如图,A,B是反比例函数y=在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A.4 B.3 C.2 D.1
【详解】∵A,B是反比例函数y=在第一象限内的图象上的两点,
且A,B两点的横坐标分别是2和4,
∴当x=2时,y=2,即A(2,2),
当x=4时,y=1,即B(4,1),
如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,
则S△AOC=S△BOD=×4=2,
∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,∴S△AOB=S梯形ABDC,
∵S梯形ABDC=(BD+AC) CD=×(1+2)×2=3,∴S△AOB=3,
故选B.
题型五(反比例函数实际应用)
1.如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(1)设V=.∵点(12,4000)在此函数图象上,∴蓄水量为12×4000=48000m3;
(2)∵点(12,4000)在此函数图象上,∴4000=,k=48000,
∴此函数的解析式V=;
(3)∵当t=6时,V==8000m3;∴每小时的排水量应该是8000m3.
题型五(反比例函数实际应用)
2.我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
(1)把B(12,20)代入中得:k=12×20=240;
(2)设AD的解析式为:y=mx+n.把(0,10)、(2,20)代入y=mx+n中得:
,解得:,
∴AD的解析式为:y=5x+10.当y=15时,15=5x+10,x=1,15=,x==16,∴16﹣1=15.
答:恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有15小时.
D
近几年来,在全国各地的中考题中,涉及一次函数、反比例函数的知识较多,尤其是求函数的解析式和利用函数的图象及性质的考题经常出现,几乎每年都有,各种题型都有。本章内容作为中考命题的热点,不仅有创新题、探究题出现,综合型大题也屡屡出现,因此,平时应多加训练,重点是与几何知识方程(组)和不等式知识的综合应用、及反比例系数的几何意义。
中考真题
1.(2022·辽宁阜新·中考真题)已知反比例函数的图像经过点,那么该反比例函数图像也一定经过点( )
A. B. C. D.
【详解】解:反比例函数的图象经过点,,
A、,此点不在反比例函数的图象上,故本选项错误;
B、,此点不在反比例函数的图象上,故本选项错误;
C、,此点在反比例函数的图象上,故本选项正确;
D、,此点不在反比例函数的图象上,故本选项错误.
故选:C.
中考真题
2.(2022·天津·中考真题)若点都在反比例函数的图像上,则的大小关系是( )
A. B. C. D.
【详解】将三点坐标分别代入函数解析式,得:
,解得;
,解得;
,解得;
∵-8<2<4,∴,故选: B.
中考真题
3.(2022·四川德阳·中考真题)一次函数y=ax+1与反比例函数在同一坐标系中的大致图象是( )
【详解】一次函数与y轴交点为(0,1),A选项中一次函数与y轴交于负半轴,故错误;
B选项中,根据一次函数y随x增大而减小可判断a<0,反比例函数过一、三象限,则-a>0,即a<0,两者一致,故B选项正确;
C选项中,根据一次函数y随x增大而增大可判断a>0,反比例函数过一、三象限,则-a>0,即a<0,两者矛盾,故C选项错误;
D选项中,根据一次函数y随x增大而减小可判断a<0,反比例函数过二、四象限,则-a<0,即a>0,两者矛盾,故D选项错误;
故选:B.
中考真题
4.(2022·江苏无锡·中考真题)一次函数y=mx+n的图像与反比例函数y=的图像交于点A、B,其中点A、B的坐标为A(-,-2m)、B(m,1),则△OAB的面积( )
A.3 B. C. D.
【详解】解:∵A(-,-2m)在反比例函数y=的图像上,∴m=(-) ( -2m)=2,
∴反比例函数的解析式为y=,∴B(2,1),A(-,-4),
把B(2,1)代入y=2x+n得1=2×2+n,∴n=-3,
∴直线AB的解析式为y=2x-3,直线AB与y轴的交点D(0,-3),∴OD=3,
∴S△AOB=S△BOD+S△AOD=×3×2+×3×=.
故选:D.
中考真题
5.(2022·湖南郴州·中考真题)如图,在函数的图像上任取一点A,过点A作y轴的垂线交函数的图像于点B,连接OA,OB,则的面积是( )
A.3 B.5 C.6 D.10
【详解】解:如图,作AD⊥x轴,BC⊥x轴,
∵,
∴
∵
∴
故选:B.
中考真题
6.(2022·四川内江·中考真题)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
【详解】解:设点P(a,b),Q(a,),则OM=a,PM=b,MQ=,
∴PQ=PM+MQ=.
∵点P在反比例函数y=的图象上,∴ab=8.
∵S△POQ=15,∴PQ OM=15,
∴a(b﹣)=15.∴ab﹣k=30.∴8﹣k=30,解得:k=﹣22.故选:D.
中考真题
7.(2022·湖北十堰·中考真题)如图,正方形的顶点分别在反比例函数和的图象上.若轴,点的横坐标为3,则( )
A.36 B.18 C.12 D.9
【详解】解:连接AC,与BD相交于点P,设PA=PB=PC=PD=t(t≠0).
∴点D的坐标为(3,),∴点C的坐标为(3-t,+t).
∵点C在反比例函数y=的图象上,∴(3-t)(+t)=k2,化简得:t=3-,
∴点B的纵坐标为+2t=+2(3-)=6-,
∴点B的坐标为(3,6-),
∴3×(6-)=,整理,得:+=18.
故选:B.
中考真题
8.(2022·浙江宁波·中考真题)如图,正比例函数的图像与反比例函数的图像都经过点.
(1)求点A的坐标和反比例函数表达式.
(2)若点在该反比例函数图像上,且它到y轴距离小于3,请根据图像直接写出n的取值范围.
中考真题
9.(2022·江苏苏州·中考真题)如图,一次函数的图像与反比例函数的图像交于点,与y轴交于点B,与x轴交于点.
(1)求k与m的值;
(2)为x轴上的一动点,当△APB的面积为时,求a的值.
(1)解:把代入,得.∴.把代入,
得.∴.把代入,得.∴k的值为,的值为6.
(2)当时,.∴.
∵为x轴上的一动点,∴.
∴,
.
∵,∴.∴或.
中考真题
10.(2022·吉林·中考真题)密闭容器内有一定质量的气体,当容器的体积(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积是反比例函数关系,它的图像如图所示.
(1)求密度关于体积的函数解析式;
(2)当时,求该气体的密度.
(1)设密度关于体积的函数解析式为,
把点A的坐标代入上式中得:,解得:k=10,∴.
(2)当时,().
即此时该气体的密度为1.
反比例函数
章节总结
第二十六章
学习目标
通过探索实际问题数量关系的过程,理解反比例函数的概念。能画出反比例函数的图象,并根据图象和解析式掌握反比例函数的主要性质,体会反比例函数在实际生活中的应用。
重点
理解反比例函数的概念和性质。
难点
理解反比例函数系数的几何意义。
反比例函数是继二次函数后又一种比较重要的函数,并且对图像的把握要求更高,我们经常会通过数形结合的方法来解决相关的题。我们要全面了解反比例函数的相关概念及性质,与一次函数对比学习,它们既有联系又有区别,其难度相对于二次函数来说是比较简单的。
基础巩固(反比例函数的定义)
一般地,形如 y = (k 为常数,且 k ≠ 0)的函数,叫做反比例函数,其中 x 是自变量,y 是函数。
【注意】1)自变量 x 的取值范围是不等于 0 的一切实数.(x=0,分式 无意义)
2)反比例函数也写成y=kx-1或k=xy的形式。
基础巩固(反比例函数的图象与性质)
当k>0时,反比例函数y = 的图象:
(1)函数图象分别位于第一、三象限;
(2)在每一个象限内,y随x的增大而减小。
当k<0时,反比例函数y = 的图象:
(1)函数图象分别位于第二、四象限;
(2)在每一个象限内,y随x的增大而增大.
形状: 图象都是由两条曲线组成,因此称反比例函数的图象为双曲线。
两个分支都无限趋近坐标轴,但不与坐标轴相交。两个分支关于原点对称。
k 的正负决定反比例函数所在的象限和增减性
基础巩固(反比例函数k的几何意义)
在一个反比例函数图象上任意取两点P,Q,过点P,Q分别作x轴和y轴的平行线,与坐标轴围成的矩形面积分别记为S1和S2,则S1和S2之间有什么关系?
s1
s2
P
Q
S1 = S2 =|k|
基础巩固(反比例函数k的几何意义)
在一个反比例函数图象上任意取两点P,Q,过点P,Q分别作x轴和y轴的平行线,与坐标轴围成的三角形面积分别记为S1和S2,则S1和S2之间有什么关系?
P
Q
S1 = S2 =
在初中数学函数中,反比例函数作为一种特殊的函数,区别于一次函数和二次函数,它的函数图像是两个断开的分支,永远不与坐标轴相交。于是关于反比例函数的题目除了一些围绕其函数性质,求k的值等题目之外,就是与几何图形联系起来出题,这类题难度较高,常作为压轴题出现。
题型一(判断反比例函数)
1. 下列关系式中,y是x的反比例函数的是 ( )
A. B. C. D.
2. 下列函数:①y=2x,②y=,③y=x﹣1,④y=.其中,是反比例函数的有( )
A.0个 B.1个 C.2个 D.3个
题型二(根据反比例函数的定义求参数)
1. 已知是关于的反比例函数,则( )
A. B. C. D.为一切实数
2. 若函数y=(m﹣1)x|m|﹣2是反比例函数,则m的值是( )
A.m=﹣1 B.m=1
C.m=﹣1或m=1 D.m=﹣2或m=2
【详解】解:由题意得:,解得m=-1,故选:A.
题型三(反比例函数的图象与性质)
1. 下列反比例函数图象一定在第一、三象限的是( )
A. B. C. D.
2. 若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
3.已知函数是反比例函数,则此反比例函数的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、四象限 D.第二、三象限
题型三(反比例函数的图象与性质)
4.在反比例函数的图象的每一个分支上,y都随x的增大而减小,则k的取值范围是( )
A.k>1 B.k>0 C.k≥1 D.k<1
5.已知反比例函数(k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx﹣k的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
题型四(反比例系数k的几何意义)
1 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A.3 B.﹣3 C.6 D.﹣6
【详解】连结OA,如图,
∵AB⊥x轴,∴OC∥AB,
∴S△OAB=S△CAB=3,而S△OAB=|k|,∴|k|=3,
∵k<0,∴k=﹣6.故选D.
题型四(反比例系数k的几何意义)
2 如图,在平面直角坐标系中,函数 y kx 与 y 的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
A.2 B.4 C.6 D.8
【详解】
连接OC,设AC⊥y轴交y轴为点D,
∵反比例函数y=-为对称图形,∴O为AB 的中点,∴S△AOC=S△COB,
∵由题意得A点在y=-上,B点在y=上,∴S△AOD=×OD×AD=xy=1;
S△COD=×OC×OD=xy=2;
S△AOC= S△AOD+ S△COD=3,
∴S△ABC= S△AOC+S△COB=6.故答案选C.
题型四(反比例系数k的几何意义)
3. 如图,A,B是反比例函数y=在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A.4 B.3 C.2 D.1
【详解】∵A,B是反比例函数y=在第一象限内的图象上的两点,
且A,B两点的横坐标分别是2和4,
∴当x=2时,y=2,即A(2,2),
当x=4时,y=1,即B(4,1),
如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,
则S△AOC=S△BOD=×4=2,
∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,∴S△AOB=S梯形ABDC,
∵S梯形ABDC=(BD+AC) CD=×(1+2)×2=3,∴S△AOB=3,
故选B.
题型五(反比例函数实际应用)
1.如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(1)设V=.∵点(12,4000)在此函数图象上,∴蓄水量为12×4000=48000m3;
(2)∵点(12,4000)在此函数图象上,∴4000=,k=48000,
∴此函数的解析式V=;
(3)∵当t=6时,V==8000m3;∴每小时的排水量应该是8000m3.
题型五(反比例函数实际应用)
2.我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
(1)把B(12,20)代入中得:k=12×20=240;
(2)设AD的解析式为:y=mx+n.把(0,10)、(2,20)代入y=mx+n中得:
,解得:,
∴AD的解析式为:y=5x+10.当y=15时,15=5x+10,x=1,15=,x==16,∴16﹣1=15.
答:恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有15小时.
D
近几年来,在全国各地的中考题中,涉及一次函数、反比例函数的知识较多,尤其是求函数的解析式和利用函数的图象及性质的考题经常出现,几乎每年都有,各种题型都有。本章内容作为中考命题的热点,不仅有创新题、探究题出现,综合型大题也屡屡出现,因此,平时应多加训练,重点是与几何知识方程(组)和不等式知识的综合应用、及反比例系数的几何意义。
中考真题
1.(2022·辽宁阜新·中考真题)已知反比例函数的图像经过点,那么该反比例函数图像也一定经过点( )
A. B. C. D.
【详解】解:反比例函数的图象经过点,,
A、,此点不在反比例函数的图象上,故本选项错误;
B、,此点不在反比例函数的图象上,故本选项错误;
C、,此点在反比例函数的图象上,故本选项正确;
D、,此点不在反比例函数的图象上,故本选项错误.
故选:C.
中考真题
2.(2022·天津·中考真题)若点都在反比例函数的图像上,则的大小关系是( )
A. B. C. D.
【详解】将三点坐标分别代入函数解析式,得:
,解得;
,解得;
,解得;
∵-8<2<4,∴,故选: B.
中考真题
3.(2022·四川德阳·中考真题)一次函数y=ax+1与反比例函数在同一坐标系中的大致图象是( )
【详解】一次函数与y轴交点为(0,1),A选项中一次函数与y轴交于负半轴,故错误;
B选项中,根据一次函数y随x增大而减小可判断a<0,反比例函数过一、三象限,则-a>0,即a<0,两者一致,故B选项正确;
C选项中,根据一次函数y随x增大而增大可判断a>0,反比例函数过一、三象限,则-a>0,即a<0,两者矛盾,故C选项错误;
D选项中,根据一次函数y随x增大而减小可判断a<0,反比例函数过二、四象限,则-a<0,即a>0,两者矛盾,故D选项错误;
故选:B.
中考真题
4.(2022·江苏无锡·中考真题)一次函数y=mx+n的图像与反比例函数y=的图像交于点A、B,其中点A、B的坐标为A(-,-2m)、B(m,1),则△OAB的面积( )
A.3 B. C. D.
【详解】解:∵A(-,-2m)在反比例函数y=的图像上,∴m=(-) ( -2m)=2,
∴反比例函数的解析式为y=,∴B(2,1),A(-,-4),
把B(2,1)代入y=2x+n得1=2×2+n,∴n=-3,
∴直线AB的解析式为y=2x-3,直线AB与y轴的交点D(0,-3),∴OD=3,
∴S△AOB=S△BOD+S△AOD=×3×2+×3×=.
故选:D.
中考真题
5.(2022·湖南郴州·中考真题)如图,在函数的图像上任取一点A,过点A作y轴的垂线交函数的图像于点B,连接OA,OB,则的面积是( )
A.3 B.5 C.6 D.10
【详解】解:如图,作AD⊥x轴,BC⊥x轴,
∵,
∴
∵
∴
故选:B.
中考真题
6.(2022·四川内江·中考真题)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
【详解】解:设点P(a,b),Q(a,),则OM=a,PM=b,MQ=,
∴PQ=PM+MQ=.
∵点P在反比例函数y=的图象上,∴ab=8.
∵S△POQ=15,∴PQ OM=15,
∴a(b﹣)=15.∴ab﹣k=30.∴8﹣k=30,解得:k=﹣22.故选:D.
中考真题
7.(2022·湖北十堰·中考真题)如图,正方形的顶点分别在反比例函数和的图象上.若轴,点的横坐标为3,则( )
A.36 B.18 C.12 D.9
【详解】解:连接AC,与BD相交于点P,设PA=PB=PC=PD=t(t≠0).
∴点D的坐标为(3,),∴点C的坐标为(3-t,+t).
∵点C在反比例函数y=的图象上,∴(3-t)(+t)=k2,化简得:t=3-,
∴点B的纵坐标为+2t=+2(3-)=6-,
∴点B的坐标为(3,6-),
∴3×(6-)=,整理,得:+=18.
故选:B.
中考真题
8.(2022·浙江宁波·中考真题)如图,正比例函数的图像与反比例函数的图像都经过点.
(1)求点A的坐标和反比例函数表达式.
(2)若点在该反比例函数图像上,且它到y轴距离小于3,请根据图像直接写出n的取值范围.
中考真题
9.(2022·江苏苏州·中考真题)如图,一次函数的图像与反比例函数的图像交于点,与y轴交于点B,与x轴交于点.
(1)求k与m的值;
(2)为x轴上的一动点,当△APB的面积为时,求a的值.
(1)解:把代入,得.∴.把代入,
得.∴.把代入,得.∴k的值为,的值为6.
(2)当时,.∴.
∵为x轴上的一动点,∴.
∴,
.
∵,∴.∴或.
中考真题
10.(2022·吉林·中考真题)密闭容器内有一定质量的气体,当容器的体积(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积是反比例函数关系,它的图像如图所示.
(1)求密度关于体积的函数解析式;
(2)当时,求该气体的密度.
(1)设密度关于体积的函数解析式为,
把点A的坐标代入上式中得:,解得:k=10,∴.
(2)当时,().
即此时该气体的密度为1.
