2022-2023人教版初中七年级数学第一章---有理数精品期末复习教案(解析版)
文档属性
| 名称 | 2022-2023人教版初中七年级数学第一章---有理数精品期末复习教案(解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 14:55:58 | ||
图片预览




文档简介
人教七上数学第一章--有理数
期末复习教学设计
课题 有理数 单元 第一章 学科 数学 年级 七年级
教材分析 第一章“有理数”的主要内容是有理数的有关概念及其运算。通过本章的学习,要使学生了解有理数产生的必要性、有理数的意义,能够进行有理数的运算,体会“数的扩张”的一致性,并能解决一些简单实际问题。
核心素养分析 本章教材注重突出学生的自主探索,通过一些熟悉的,具体的事物,让学生在观察、思考、探索中体会有理数的意义,探索数量关系,掌握有理数的运算方法及其教育价值。
学习 目标 1.理解有理数的意义,能用数轴上的点表示有理数,能比较有理数的大小。 2.能借助数轴理解相反数和绝对值的意义,掌握求有理数的相反数和绝对值的方法。 3.理解 乘方的意义,掌握有理数的加、减、乘、除、乘方及简单的混合运算。 4.理解有理数的运算律,能用运算律简化运算。 5.能运用有理数的运算解决简单的问题。
重点 1.有理数的概念,大小比较和绝对值的概念 2.数轴的建立以及利用数轴建立起来的数形结合的数学思想 3.通过多有理数的运算和运算律的学习,提高学生的计算能力
难点 通过数轴、相反数、绝对值的学习,让学生在体验数形结合思想的同时,提高数学抽象能力。
第一章 有理数
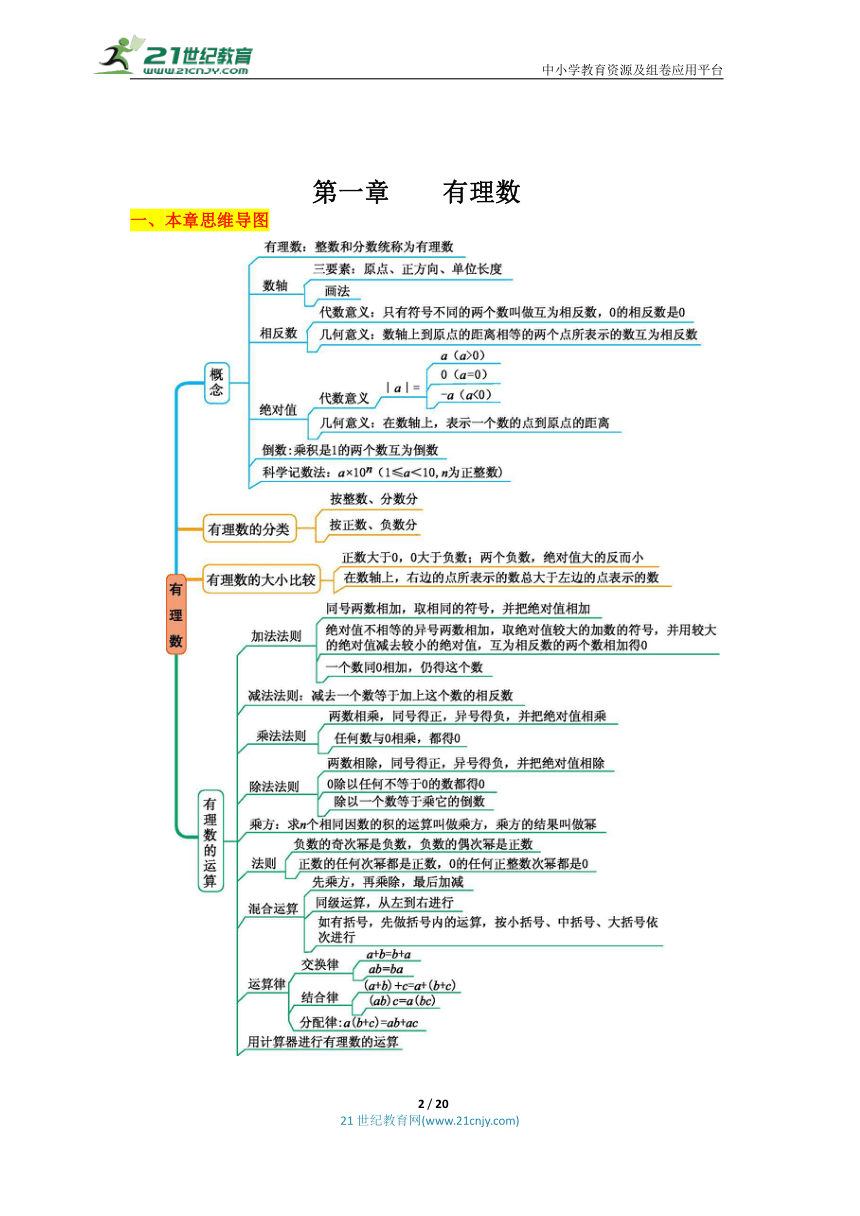
一、本章思维导图
二、本章考点复习
知识点一、正数和负数
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
1 / 13
考点1、正数和负数的概念
概念 正数:像8844、、0.5、10%、2022.........这样大于0的数. (数前面的“+”一般省略) (1)读法:如“+5”读作:“正5”或“5”. (2)符号“+”:作为运算符号是加号,作为性质符号是正号.作为符号可以省略不写. 负数:像—11034、— 、—0.5、—10%......这样在正数前面加上符号“—(负)”的数.(负号“—”不可省略)-------小于0的数. (1)读法:如“—8”读作:负8. (2)符号“—”:作为运算符号是减号,作为性质符号是负号.作为符号不可省略. 规定:“0”既不是正数,也不是负数. “+”可省略,“—”不能省略.
注意 正数和负数在书写时的区别: 正数前的“+”号可以省略,负前的“-”号一定不能省略! (2)在引入负数以后,“0”还表示“+”与“-”之间的分界点.
拓展 1.+”“-”的双重意义: ①作为运算符号是加、减号; ②作为数的性质符号是正、负号. 2. 带“+”号的数不一定是正数,带“-”号的数也不一定是负数. 3.正、负数的识别方法:不能简单的看“+”和“-”来判别正数和负数. (1)a>0,则a是正数,-a表示负数; (2)a<0,则a是负数,-a表示正数;
考点2、对“0”的认识
1.从数上看:
(1)0既不是正数,也不是负数,0是正数和负数的分界,是正负数的基准.
(2)负数<0<正数.
(3)0和正数统称为非负数,非负数a0.
(4)0和负数统称为非正数,非正数a0.
2.从实际意义上看:0不再仅仅表示没有,它具有丰富的意义:空罐里金币的数量、温度中的0℃、海平面的高度、标准水位、身高比较的基准……
考点3、用正数和负数表示具有相反意义的量
含义 (1)具有相反意义;(2)数量.
方法 具有相反意义的量:为了表示具有相反意义的量,我们把表示其中一种意义的量规定为正,用正数表示,那么与它意义相反的量就可以用负数表示.
特别提醒 具有相反意义的量的表述: 具有相反意义的量必须是成对出现的,单独一个量不能成为具有相 反意义的量.
(2)具有相反意义的量必须具备两个条件: 一是两个量所表示的属性相同,即表示的是同一类对象,也就是说这 两个量的单位相同; 二是两个量所表示的意义恰好相反. 具有相反意义的量的正负性是相对的,且是可以互换的. 描述一对具有相反意义的量的词语一般是一对反义词,如上升与下降,增加与减少,向东和向西,盈利与亏损,收入与支出等 用正数和负数表示具有相反意义的量时,哪种意义为正是可以任意 择的,但习惯上把“前进、上升、收入、零上温度”等规定为正,而把“后退、下降、支出、零下温度”等规定为负.
注意 具有相反意义的量,只要求意义相反,而不要求数量一定相等,所以与 一个量成意义相反的量不止一个。
知识点二、有理数
考点1.有理数的概念
(1)定义:整数和分数统称为有理数.
(2)注意:
①概念中所用“统称”二字,它与说“整数和分数是有理数”的意思不大一样.
前者回避了分数是否包括整数的问题,即使把整数包括在分数范围内,说“统称”还是不错,而用后一种说法就欠妥了.
②分数(既约分数)都可表示成小数,但不是所有的小数都能表示成分数的.如圆周率就不能表示成分数.
有限小数和无限循环小数都可以化成分数,所以把有限小数和无限循环小
数看成分数.
拓展:无理数:无限不循环小数.
四类无理数:
无限不循环小数:0.1010010001……
π或与π相关的:π+1,,……
开方开不尽的数:,,……
三角函数:sin45°……
注意:π≠3.14,不取近似,除非题目要求,含π的都是无理数.
(2)引入负数后,对数的认识扩充到有理数,不要忘记整数和分数中都有
负数.
考点2.有理数的分类及“六非”
(1) 按有理数的概念分类: (2)按有理数的性质分类:
先按定义,再按符号 先按符号,在按定义
有理数 有理数
注意:0.25是分数,但 不是分数,是整数.
Eg: 判断:①正数和负数统称为有理数.(× 还有0,π,等)
②正数、负数和0统称为有理数.(× 比如π)
注意:
(1)有理数分类,分类的标准不同,分类的结果就不同,所以要按统一
标准分类;
(2)要想分类结果不重复、无遺漏,必须掌握两种分类标准,“整”和“分”
对应,“正”与“负”对应;0既不是正数也不是负数,它是整数也是有理数.
(3)圆周率π是正数,但不是有理数,千万要注意,类似,-等同样
也不是有理数.
(4)对有理数进行分类时,不要把两个标准混淆,也千万不要忽略0.
(5)遇到无限不循环小数要当心,要防止它混入有理数的队伍,尤其小心最容易被迷惑.
相关的六非:
非正数:0和负数
非负数:0和正数
非正整数:0和负整数
非负整数:0和正整数
非正有理数:0和负有理数
非负有理数:0和正有理数
注意:(1)“非”否点的只是符号,可用加“的”.如:非正“的”整数.
(2)有“非”就有0.
知识点三、数轴
考点1.数轴的概念
1.定义:规定了原点、正方向和单位长度的直线叫做数轴.
2.注意:
①数轴可以向两端无限延伸.
②数轴的三要素:原点、正方向、单位长度缺一不可.
③原点的位置,正方向的选择,单位长度大小这三个要素都是根据实际需
要确定的.
④数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上
的点所表示的数并不都是有理数.
特别提醒:
单位长度和长度单位不是一回事.单位长度可以任意选取,而长度单位是我
们在小学学过的一些为了规范长度而制定的基本单位,如m,dm,cm.
同一数轴中的单位长度一定要统一.
(3)原点、正方向、单位长度大小的确定都是根据实际需要“规定”的.如在确定
原点的位置时,若负数的个数较多,则原点选得靠右些,反之亦然.
考点2.数轴的画法:
(1)画直线(一般画成水平的)、定原点,标出原点“O”.
(2)取原点向右方向为正方向,并标出箭头.
(3)选适当的长度作为单位长度,并标出…,-3,-2,-1,1,2,3…各点.具体如下图.
(4)标注数字时,负数的次序不能写错,如下图.
考点3.数轴上的点与有理数的关系
1.一切有理数都可以用数轴上的点表示出来.
2.在数轴上,右边的点所对应的数总比左边的点所对应的数大.
3.正数都在数轴的右边,正数大于0;负数都在数轴的左边,负数都小于0;正数大于一切负数.
4.注意:数轴上的点不都代表有理数,如.
考点4.数轴的应用:
(1)用数轴上点表示有理数.
(2)用数轴比较有理数的大小:
①由正、负数在数轴上的位置可知:
正数都有大于0,负数都小于0,正数大于一切负数.
②右边的数总比左边的数大.
③比较大小时,用不等号顺次连接三个数要防止出现 的写法,正确应写成.
(3)用数轴解决与相反数和绝对值有关的问题:距离问题
a.有图有真像:
b.无图双方向:
特别提醒:
(1)数轴上的点并不都表示有理数.也就是说,数轴上的点与有理数并不是一一
对应关系.
(2)设a是一个正数,则数轴上表示a的点在原点的右边,与原点的距离是a
个单位长度;表示-a的点在原点的左边,与原点的距离也是a个单位长度.
当a是0时,表示数a的点就是原点.
知识点四、相反数
考点1.相反数的概念
(1)代数定义:像2和-2,5和-5这样,只有符号不同的两个数叫作互为相反数,把其中一个数叫作另一个数的相反数,如-2022是2022的相反数.
(2)几何定义:在数轴上,位于原点两旁,且与原点距离相等的两点关于原点对称,所表示的两个数互为相反数.
另外还规定,0的相反数是0.
(3)表示:一个数前面放上一个“+”,得到的仍是这个数;一个数前面放上一个“-”,得到的就是它的相反数.
注意:
(1)任何一个数都有相反数,而且只有一个.
(2)相反数是表示两个数的相互关系,不能单独存在.
(3)互为相反数的两个数只有符号不同.
特别提醒:
符号(相反)不同,数值(绝对值)相同.
成对出现(夫妻数)相反数是成对出现的,不能单独存在.单独的一个数不能说是相反
数.
考点2.求一个数的相反数
方法:在一个数的前面添上“-”号就成为原数的相反数.
若 表示一个有理数,则 的相反数表示为- .
在一个数的前面添上“+”号仍与原数相同.
例如,+7=7,特别地,+0=0,-0=0.
求一个数的相反数,只要在这个数的前面加上“—”即可.
考点3.多重符号的化简
(1)当最前面的符号是“+”,可以直接省略不写.
(2)当一个数的前面有奇数个负号,则这个数是负数;
一个正数的前面有偶数的负号,则这个数是正数.简称“奇负偶正”.
①奇、偶:“—”的个数;
②正、负:结果的符号。
注意:只能推出结果符号的正负:—(—a)=a,要看a的正负.
考点4.互为相反数的性质
(1)若 互为相反数,则 ;反之若 ,则 互为相反数.
(2)若两个数互为相反数,则这两个数位于原点的两侧,且到原点的距离相等.
(3)正数的相反数是负数,即当有理数a>0,则-a<0
(4)负数的相反数是在正数,即当有理数a<0,则-a>0.
(5)0的相反数是0.也只有0的相反数是它的本身.
知识点五、绝对值
概念 数轴上表示数a的点到原点的距离叫做数a的绝对值,记作|a|. 我们规定,0的绝对值是0,记作|0|=0. 1.绝对值的几何意义:数轴上表示数的点与原点的距离.数的绝对 值记作.读作“a的绝对值”. 2.绝对值的代数意义:一个正数的绝对值是它本身; 一个负数的绝对值是它的相反数; 0的绝对值是0.
法则 有理数绝对值的求法: 正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0. 也就是: 当a是正数时,|a|=a;当a是负数时,|a|=-a;当a是0时,|a|=0. 求数的绝对值: ① ; ② ; ③.
注意 表示一个数的点与原点的距离越远,这个数的绝对值越大,与原点 的距离越近,这个数的绝对值越小.
(2)距离不可能是负数,故任何数的绝对值都是非负数.
(3)绝对值是某个正数的数有两个,它们互为相反数,如绝对值是2的 数有2和-2.
拓展 互为相反数的两个数的绝对值相等.反过来绝对值相等的两个数相等或互为相反数.例如,若a和b互为相反数,则|a|=|b|;若|a|=|b|,则a=b或a=-b.
注意 ①取绝对值也是一种运算,运算符号是“”,求一个数的绝对值,就是 根据性质去掉绝对值符号. ②任何一个有理数都是由两部分组成:符号和它的绝对值,如:符号 是负号,绝对值是.
二、绝对值的性质:
1.绝对值具有非负性,取绝对值的结果总是正数或0,即.在实数范围内,
绝对值最小的数是零.
2.在数轴上,一个数离原点越近,绝对值越小;离原点越远,绝对值越大.
3.一个数的绝对值要么等于它本身,要么等于它的相反数:
若则;若.
4.绝对值是某个正数的数有两个,它们互为相反数,即若,则.
即,则.
5.互为相反数的两个数的绝对值相等;绝对值相等的两个数相等或互为相反数.即若,则或.
6.任何实数都有唯一绝对值,并且任何一个实数都不大于它的绝对值,即.且.
三、绝对值非负性的应用
如果若干个非负数的和为0,那么若干个非负数都必为0.
例如:若,则,,.
四、绝对值的其它重要性质:
(1)任何一个数的绝对值都不小于这个数,也不小于这个数的相反数,即,
(2);;
当时,
当时,
若,则
(3);
(4),
对于,等号当且仅当、同号或、中至少有一个时,等号成立;
对于,等号当且仅当、异号或、中至少有一个时,等号成立.
知识点六、有理数的四则运算
考点1.有理数的加法
1.有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加.
(2)异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
(3)互为相反的两数相加的0(若a、b互为相反数,则a+b=0).
(4)一个数同0相加,仍得这个数.
2. 有理数的加法运算律:
(1)加法交换律:两个数相加,交换加数的位置,和不变.a+b=b+a
(2)加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
a+b+c=a+(b+c)=b+(a+c)
考点2.有理数的减法
有理数的减法法则:减去一个数,等于加这个数的相反数.a-b=a+(-b).
考点3.有理数的乘法
1.有理数的乘法法则:
(1)两数相乘,同号得正,异号得负,并把绝对值相乘.
(2)任何数与0相乘都得0.
2.有理数的倒数:乘积为1的两个数互为倒数.
3.多个有理数相乘:
(1)几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.
(2)几个有理数相乘,如果其中有一个因数为0,那么积为0.
4.有理数的乘法运算律:
(1)乘法交换律:两个数相乘,交换因数的位置,积不变.
(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.
(3)分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
总结:奇负偶正,先把带分数化成假分数再乘;
分配律、结合律、交换律的灵活应用.
考点4.有理数的除法
有理数的除法法则:
1.除以一个不等于0的数,等于乘这个数的 倒数.
2.两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
除法易错点:①除法没有分配律;
②“单÷多”形式问题两种解法: (1)先将括号里面通分运算出结果,然后按顺序进行计算
(
(2)先计算原式的倒数,求解之后再取倒数即为原式的结果
)
考点5.有理数的乘除混合运算
1.一般将除法转化为乘法;
2.确定积的符号;
3.最后求出结果.
知识点六、有理数的乘方
1.乘方的定义:
求n 个相同因数的积的运算,叫做乘方, 乘方的结果叫做幂.在an中,a 叫
做底数,n 叫做指数.
2.注意:(1)一个数可以看做是这个数本身的一次方,指数1通常省略不写.
(2)因为an就是n个a相乘,所以可以利用乘法运算计算乘方运算.
3.乘方运算的符号法则:
(1)负数的奇次幂是负数,负数的偶次幂的正数.
(2)正数的任何次幂都是正数.
(3)0的任何正整数次幂都是0.
几个常见的易错点:
; ; ; ;
(注意:考试当中一定要注意有无括号,指数的位置)
知识点七、有理数的混合运算
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号,中括号,大括号依次进行.
知识点八、科学计数法、近似数和有效数字
一、科学计数法:
1.定义:把一个大于10的数表示成 的形式(其中a是整数位只有一位的数,n是原数的整数位减1.即1≤|a|<10,n是正整数),这种计数方法叫做科学记数法.(对于小于-10的数也可以类似的表示)
例如:就是科学记数法表示数的形式.
也是科学记数法表示数的形式.
2.注意:(1)用科学计数法只改变数的形式,不改变数的大小.
(2)当把一个用科学计数法 表示的数还原为原数时,只需将小数点向右移动n位(不足的数位用0补齐),并把10n去掉.
二、准确数与近似数
1.准确数:确切地反应了实际的数是一个准确数.
2.近似数:与实际数接近,但有差别的数是一个近似数.
3.近似数的精确度:一个数只是接近实际数,但与实际数还有差别,它是一个近似数。 近似数与准确数的接近程度,可以用精确度表示.一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位.
4.近似数的精确度的表示方法:
①用数位表示:如精确到千位或千分位
②用小数点表示:如精确到0.1或0.01等
③对带有单位的数用单位表示:如精确到千克、米等.
5.注意:万,亿.
三、题型归纳,方法技巧总结
题型一、用正、负数表示具有相反意义的量 1.此类题型解题的关键是弄清楚各问题的“基准”. 对于有基准的问题,要建立表示相反意义的正、负数与实际问题中的相关量之间的关系,从而解决问题.同时,注意0是正数与负数的分界,但并不是所有的分界都是0.
2.在实际生产、生活中,常用“±”表示某个量的允许值的范围,一般约定“+”表示“多出”或“超过”,“—”表示“少于”或“不够”.如用“a±x”表示某个量的范围,其中a表示标准数量,±x表示允许在标准数量上变动的范围.
例题1.用正负数表示具有相反意义的量.
(1)如果零上8 ℃记为+8 ℃,那么-9 ℃表示的意义是_______________ ___;
(2)如果下降了10m记为-10米,那么上升6m记为_ _____________________;
(3)如果前进25km记为+25km,那么后退8km记为___ _________________;
(4)淘淘的妈妈开的超市,今天营利为500元,记作+500元,那么昨天亏损40元记作_______.
【解析】
(1)基准是0℃,零上记为正,零下记为负;
(2)基准是水位不升也不降,下降记为负,上升记为正;
(3)基准是原地不动,前进记为正,后退记为负;
(4)基准是不亏也不赚,盈利记为正,亏损记为负.
【答案】(1)零下9 ℃; (2)+6m;(3)-8km;(4)-40元.
例题2.一袋面粉的质量标识为“25±0.25千克”,则下列面粉中合格的有( )
A.24.70千克 B.25.30千克 C.25.51千克 D.24.80千克
【解析】 “25±0.25千克”的含义是这袋面粉的质量在(25-0.25)千克与(25+0.25)千克之间,即24.75—25.25千克.只要面粉的质量在24.75—25.25千克之间就是合格产品.
【答案】D.
题型二、有理数的大小比较 1.代数法:负数<0<正数. 2.数轴法:数轴上右边的数比左边的数大. 3.绝对值法:对于两个负数,绝对值大的反而小. 4.作差法:,,. 5.作商法:若,,, ,. 6.取倒法:分子一样,通过比较分母从而判定两数的大小. 7.特殊值法:给题目中的字母一个特定的值,然后代入求值,进而比较大小.
例题3.实数在数轴上的对应点如图所示,试比较的大小
【解析】数轴法,作差法,倒数法.根据在数轴上的位置可知,,所以.
【答案】.
例题4.在数轴上表示下列各数,再按大小顺序用“<”号连接起来.
,,,,,,,
【解析】⑴先画出数轴,在数轴上方标注所求数(如图下所示),根据数轴上的大小顺序,按从左到右依次用“<”号连接起来.
即:
【答案】.
例题5.实数在数轴上的对应点如图,试比较的大小.
【解析】根据在数轴上的位置可知,,且的绝对值比的绝对值大,由数轴,作差法得.
【答案】
题型三、数轴的应用 1.数轴上点的移动问题: 可以转化为有理数的加减运算,当初始点未知时,只需要设元解简单方程即可.
2.整点覆盖问题: 线段长为个单位长度,当线段端点在数轴的整数位置覆盖点最多为,当无线段端点在在数轴整点时覆盖点最少.
3.确定原点问题: 将所有点所对应的数用同一个未知数的代数式表示.
4.数轴上两点间的距离为两点对应数的差的绝对值,注意数轴上到已知点距离为定值的点有两个,这个易错点,做题时应当特别小心.
5.数轴上线段定值问题: 数轴上常常会出现动点运动过程中产生定线段或线段和差为定值,这类问题一般通过表示出线段的表达式代入计算即可证明.
6.数轴的折叠问题: 数轴折叠过程中要搞清楚,两对应点与折痕处点的基本规律,即折痕对应点为中点,若两对应点分别记为m、n(m>n),中点记为x, 则:m-x=x-n,所以
7.数轴找规律问题:图形(圆、正方形、等边三角形)在旋转的过程中,根据图形周长有几个单位长度,每旋转一周即循环一次,即可找出对应的规律.
8.数轴上的动点运动问题:这类问题考查了规律型:认真观察、仔细思考,找出点表示的数的变化规律是解题关键.
题型四、绝对值的化简求值
1.条件型绝对值化简
例题6. 已知,化简.
【解析】因为,所以,原式.
【答案】.
2.绝对值零点分段化简
(1)零点的定义:当时,,此时是的零点值.
(2)零点分段讨论的一般步骤:
找零点、分区间、定符号、去绝对值符号.
即先令各绝对值式子为零,求得若干个绝对值为零的点,在数轴上把这些点标出来,这些点把数轴分成若干部分,再在各部分内化简求值.
例题7.化简:(1);(2)
【解析】绝对值零点分段化简,分类讨论.
【答案】(1)原式.(2)原式.
3.分式型绝对值化简:
由绝对值的定义及性质化简:若,则;若,则.
例题8.求下列代数式的值:
(1) _;(2) ;
(3) _____;(4) _____ .
(5) ____ ____;(6) _________ .
【解析】由,则;若,则进行分类讨论化简.
【答案】
(1)、.(2)、.
(3)、、.(4)、、.
(5)原式,将换元本质就与(2)完全相同,
∴原式=、.
(6)原式将、换元本质就与(3)完全相同.∴原式=、、.
题型五、绝对值的实际应用
1.绝对值的几何意义:
(1)|a|的几何意义是:数轴上表示a的点到原点的距离;
(2)|a-b|的几何意义是:数轴上表示数a、b的两点的距离.
例题9.下面材料:已知点A、B在数轴上分别表示有理数、,A、B两点之间的距离表示为.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,
当A、B两点都不在原点时:
(1) 如图2,点A、B都在原点的右边,
(2) 如图3,点A、B都在原点的左边,
(3) 如图4,点A、B在原点的两边,
综上,数轴上A、B两点的距离
回答下列问题:
(1) 数轴上表示-2和-5两点之间的距离是 ;
(2) 数轴上表示和-1的两点A、B之间的距离是,如果,那么为 ;
(3) 当代数式取最小值时,相应的x的取值范围是 .
【解析】由绝对值的几何意义可得.
【答案】(1) 3 ; (2) 1或 ; (3)
2.绝对值之和定值、最值的探讨:
设是常数(是大于的整数),且,是任意实数,求的最小值的一般方法.
根据题意,结合数轴,不难得到:
⑴当为奇数时,取“中间点”:即当(为正整数)时,点应取在 点处,原式的值最小,最小值为
⑵当为偶数时,取“中间段”:即n=(是正整数)时,应取点和点之间的任意位置,原式的值最小,最小值为.
例题10.小红和小明在研究绝对值的问题时,碰到了下面的问题:
“当式子取最小值时,相应的x的取值范围是 ,最小值是 ”.
小红说:“如果去掉绝对值问题就变得简单了。”小明说:“利用数轴可以解决这个问题。”他们把数轴分为三段:,和,经研究发现,当时,值最小为3.
请你根据他们的解题解决下面的问题:
(1)当式子取最小值时,相应的x的取值范围是 ,最小值是 .
(2)已知,求相应的x的取值范围及的最大值。写出解答过程。
【解析】(1),8 ;(2)当时,.
题型六、有理数的速算和巧算
“归”:将同类数(如正数或负数)归类计算.
“消”:将相加得0的数(如互为相反数的数)对消.
“凑”将相加可得整数的数凑整,
“合”:将不同类数(如分母相同或易于通分的数)分别组合.
“分”:将一个数分解成几个数之和的形式,或分解为它的因数相乘的形式.
“化”:将小数与分数或乘法与除法相互转化.
“变”:利用运算定律把运算顺序改变,从而简化计算.
“约”:将互为倒数的数或有因数和倍数关系的数约简.
“逆”:正难则反,逆用运算律以简化运算.
“观”:根据0和1在运算中的特性,注意观察算式特征,可收到事半功倍的效果.
裂项相消:注意观察分母上相乘的两数之差与分子是否相同。若相同,直接裂项;若不相同,需要先在整体前面乘上相对应的分数.
例如:
例题10.速算巧算.
(1).
(2)
(3)
(4)
(5)
(6)
【答案】(1)
(2)原式=
(3)原式=
(4)原式
(5)原式=
(6)原式
期末复习教学设计
课题 有理数 单元 第一章 学科 数学 年级 七年级
教材分析 第一章“有理数”的主要内容是有理数的有关概念及其运算。通过本章的学习,要使学生了解有理数产生的必要性、有理数的意义,能够进行有理数的运算,体会“数的扩张”的一致性,并能解决一些简单实际问题。
核心素养分析 本章教材注重突出学生的自主探索,通过一些熟悉的,具体的事物,让学生在观察、思考、探索中体会有理数的意义,探索数量关系,掌握有理数的运算方法及其教育价值。
学习 目标 1.理解有理数的意义,能用数轴上的点表示有理数,能比较有理数的大小。 2.能借助数轴理解相反数和绝对值的意义,掌握求有理数的相反数和绝对值的方法。 3.理解 乘方的意义,掌握有理数的加、减、乘、除、乘方及简单的混合运算。 4.理解有理数的运算律,能用运算律简化运算。 5.能运用有理数的运算解决简单的问题。
重点 1.有理数的概念,大小比较和绝对值的概念 2.数轴的建立以及利用数轴建立起来的数形结合的数学思想 3.通过多有理数的运算和运算律的学习,提高学生的计算能力
难点 通过数轴、相反数、绝对值的学习,让学生在体验数形结合思想的同时,提高数学抽象能力。
第一章 有理数
一、本章思维导图
二、本章考点复习
知识点一、正数和负数
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
1 / 13
考点1、正数和负数的概念
概念 正数:像8844、、0.5、10%、2022.........这样大于0的数. (数前面的“+”一般省略) (1)读法:如“+5”读作:“正5”或“5”. (2)符号“+”:作为运算符号是加号,作为性质符号是正号.作为符号可以省略不写. 负数:像—11034、— 、—0.5、—10%......这样在正数前面加上符号“—(负)”的数.(负号“—”不可省略)-------小于0的数. (1)读法:如“—8”读作:负8. (2)符号“—”:作为运算符号是减号,作为性质符号是负号.作为符号不可省略. 规定:“0”既不是正数,也不是负数. “+”可省略,“—”不能省略.
注意 正数和负数在书写时的区别: 正数前的“+”号可以省略,负前的“-”号一定不能省略! (2)在引入负数以后,“0”还表示“+”与“-”之间的分界点.
拓展 1.+”“-”的双重意义: ①作为运算符号是加、减号; ②作为数的性质符号是正、负号. 2. 带“+”号的数不一定是正数,带“-”号的数也不一定是负数. 3.正、负数的识别方法:不能简单的看“+”和“-”来判别正数和负数. (1)a>0,则a是正数,-a表示负数; (2)a<0,则a是负数,-a表示正数;
考点2、对“0”的认识
1.从数上看:
(1)0既不是正数,也不是负数,0是正数和负数的分界,是正负数的基准.
(2)负数<0<正数.
(3)0和正数统称为非负数,非负数a0.
(4)0和负数统称为非正数,非正数a0.
2.从实际意义上看:0不再仅仅表示没有,它具有丰富的意义:空罐里金币的数量、温度中的0℃、海平面的高度、标准水位、身高比较的基准……
考点3、用正数和负数表示具有相反意义的量
含义 (1)具有相反意义;(2)数量.
方法 具有相反意义的量:为了表示具有相反意义的量,我们把表示其中一种意义的量规定为正,用正数表示,那么与它意义相反的量就可以用负数表示.
特别提醒 具有相反意义的量的表述: 具有相反意义的量必须是成对出现的,单独一个量不能成为具有相 反意义的量.
(2)具有相反意义的量必须具备两个条件: 一是两个量所表示的属性相同,即表示的是同一类对象,也就是说这 两个量的单位相同; 二是两个量所表示的意义恰好相反. 具有相反意义的量的正负性是相对的,且是可以互换的. 描述一对具有相反意义的量的词语一般是一对反义词,如上升与下降,增加与减少,向东和向西,盈利与亏损,收入与支出等 用正数和负数表示具有相反意义的量时,哪种意义为正是可以任意 择的,但习惯上把“前进、上升、收入、零上温度”等规定为正,而把“后退、下降、支出、零下温度”等规定为负.
注意 具有相反意义的量,只要求意义相反,而不要求数量一定相等,所以与 一个量成意义相反的量不止一个。
知识点二、有理数
考点1.有理数的概念
(1)定义:整数和分数统称为有理数.
(2)注意:
①概念中所用“统称”二字,它与说“整数和分数是有理数”的意思不大一样.
前者回避了分数是否包括整数的问题,即使把整数包括在分数范围内,说“统称”还是不错,而用后一种说法就欠妥了.
②分数(既约分数)都可表示成小数,但不是所有的小数都能表示成分数的.如圆周率就不能表示成分数.
有限小数和无限循环小数都可以化成分数,所以把有限小数和无限循环小
数看成分数.
拓展:无理数:无限不循环小数.
四类无理数:
无限不循环小数:0.1010010001……
π或与π相关的:π+1,,……
开方开不尽的数:,,……
三角函数:sin45°……
注意:π≠3.14,不取近似,除非题目要求,含π的都是无理数.
(2)引入负数后,对数的认识扩充到有理数,不要忘记整数和分数中都有
负数.
考点2.有理数的分类及“六非”
(1) 按有理数的概念分类: (2)按有理数的性质分类:
先按定义,再按符号 先按符号,在按定义
有理数 有理数
注意:0.25是分数,但 不是分数,是整数.
Eg: 判断:①正数和负数统称为有理数.(× 还有0,π,等)
②正数、负数和0统称为有理数.(× 比如π)
注意:
(1)有理数分类,分类的标准不同,分类的结果就不同,所以要按统一
标准分类;
(2)要想分类结果不重复、无遺漏,必须掌握两种分类标准,“整”和“分”
对应,“正”与“负”对应;0既不是正数也不是负数,它是整数也是有理数.
(3)圆周率π是正数,但不是有理数,千万要注意,类似,-等同样
也不是有理数.
(4)对有理数进行分类时,不要把两个标准混淆,也千万不要忽略0.
(5)遇到无限不循环小数要当心,要防止它混入有理数的队伍,尤其小心最容易被迷惑.
相关的六非:
非正数:0和负数
非负数:0和正数
非正整数:0和负整数
非负整数:0和正整数
非正有理数:0和负有理数
非负有理数:0和正有理数
注意:(1)“非”否点的只是符号,可用加“的”.如:非正“的”整数.
(2)有“非”就有0.
知识点三、数轴
考点1.数轴的概念
1.定义:规定了原点、正方向和单位长度的直线叫做数轴.
2.注意:
①数轴可以向两端无限延伸.
②数轴的三要素:原点、正方向、单位长度缺一不可.
③原点的位置,正方向的选择,单位长度大小这三个要素都是根据实际需
要确定的.
④数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上
的点所表示的数并不都是有理数.
特别提醒:
单位长度和长度单位不是一回事.单位长度可以任意选取,而长度单位是我
们在小学学过的一些为了规范长度而制定的基本单位,如m,dm,cm.
同一数轴中的单位长度一定要统一.
(3)原点、正方向、单位长度大小的确定都是根据实际需要“规定”的.如在确定
原点的位置时,若负数的个数较多,则原点选得靠右些,反之亦然.
考点2.数轴的画法:
(1)画直线(一般画成水平的)、定原点,标出原点“O”.
(2)取原点向右方向为正方向,并标出箭头.
(3)选适当的长度作为单位长度,并标出…,-3,-2,-1,1,2,3…各点.具体如下图.
(4)标注数字时,负数的次序不能写错,如下图.
考点3.数轴上的点与有理数的关系
1.一切有理数都可以用数轴上的点表示出来.
2.在数轴上,右边的点所对应的数总比左边的点所对应的数大.
3.正数都在数轴的右边,正数大于0;负数都在数轴的左边,负数都小于0;正数大于一切负数.
4.注意:数轴上的点不都代表有理数,如.
考点4.数轴的应用:
(1)用数轴上点表示有理数.
(2)用数轴比较有理数的大小:
①由正、负数在数轴上的位置可知:
正数都有大于0,负数都小于0,正数大于一切负数.
②右边的数总比左边的数大.
③比较大小时,用不等号顺次连接三个数要防止出现 的写法,正确应写成.
(3)用数轴解决与相反数和绝对值有关的问题:距离问题
a.有图有真像:
b.无图双方向:
特别提醒:
(1)数轴上的点并不都表示有理数.也就是说,数轴上的点与有理数并不是一一
对应关系.
(2)设a是一个正数,则数轴上表示a的点在原点的右边,与原点的距离是a
个单位长度;表示-a的点在原点的左边,与原点的距离也是a个单位长度.
当a是0时,表示数a的点就是原点.
知识点四、相反数
考点1.相反数的概念
(1)代数定义:像2和-2,5和-5这样,只有符号不同的两个数叫作互为相反数,把其中一个数叫作另一个数的相反数,如-2022是2022的相反数.
(2)几何定义:在数轴上,位于原点两旁,且与原点距离相等的两点关于原点对称,所表示的两个数互为相反数.
另外还规定,0的相反数是0.
(3)表示:一个数前面放上一个“+”,得到的仍是这个数;一个数前面放上一个“-”,得到的就是它的相反数.
注意:
(1)任何一个数都有相反数,而且只有一个.
(2)相反数是表示两个数的相互关系,不能单独存在.
(3)互为相反数的两个数只有符号不同.
特别提醒:
符号(相反)不同,数值(绝对值)相同.
成对出现(夫妻数)相反数是成对出现的,不能单独存在.单独的一个数不能说是相反
数.
考点2.求一个数的相反数
方法:在一个数的前面添上“-”号就成为原数的相反数.
若 表示一个有理数,则 的相反数表示为- .
在一个数的前面添上“+”号仍与原数相同.
例如,+7=7,特别地,+0=0,-0=0.
求一个数的相反数,只要在这个数的前面加上“—”即可.
考点3.多重符号的化简
(1)当最前面的符号是“+”,可以直接省略不写.
(2)当一个数的前面有奇数个负号,则这个数是负数;
一个正数的前面有偶数的负号,则这个数是正数.简称“奇负偶正”.
①奇、偶:“—”的个数;
②正、负:结果的符号。
注意:只能推出结果符号的正负:—(—a)=a,要看a的正负.
考点4.互为相反数的性质
(1)若 互为相反数,则 ;反之若 ,则 互为相反数.
(2)若两个数互为相反数,则这两个数位于原点的两侧,且到原点的距离相等.
(3)正数的相反数是负数,即当有理数a>0,则-a<0
(4)负数的相反数是在正数,即当有理数a<0,则-a>0.
(5)0的相反数是0.也只有0的相反数是它的本身.
知识点五、绝对值
概念 数轴上表示数a的点到原点的距离叫做数a的绝对值,记作|a|. 我们规定,0的绝对值是0,记作|0|=0. 1.绝对值的几何意义:数轴上表示数的点与原点的距离.数的绝对 值记作.读作“a的绝对值”. 2.绝对值的代数意义:一个正数的绝对值是它本身; 一个负数的绝对值是它的相反数; 0的绝对值是0.
法则 有理数绝对值的求法: 正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0. 也就是: 当a是正数时,|a|=a;当a是负数时,|a|=-a;当a是0时,|a|=0. 求数的绝对值: ① ; ② ; ③.
注意 表示一个数的点与原点的距离越远,这个数的绝对值越大,与原点 的距离越近,这个数的绝对值越小.
(2)距离不可能是负数,故任何数的绝对值都是非负数.
(3)绝对值是某个正数的数有两个,它们互为相反数,如绝对值是2的 数有2和-2.
拓展 互为相反数的两个数的绝对值相等.反过来绝对值相等的两个数相等或互为相反数.例如,若a和b互为相反数,则|a|=|b|;若|a|=|b|,则a=b或a=-b.
注意 ①取绝对值也是一种运算,运算符号是“”,求一个数的绝对值,就是 根据性质去掉绝对值符号. ②任何一个有理数都是由两部分组成:符号和它的绝对值,如:符号 是负号,绝对值是.
二、绝对值的性质:
1.绝对值具有非负性,取绝对值的结果总是正数或0,即.在实数范围内,
绝对值最小的数是零.
2.在数轴上,一个数离原点越近,绝对值越小;离原点越远,绝对值越大.
3.一个数的绝对值要么等于它本身,要么等于它的相反数:
若则;若.
4.绝对值是某个正数的数有两个,它们互为相反数,即若,则.
即,则.
5.互为相反数的两个数的绝对值相等;绝对值相等的两个数相等或互为相反数.即若,则或.
6.任何实数都有唯一绝对值,并且任何一个实数都不大于它的绝对值,即.且.
三、绝对值非负性的应用
如果若干个非负数的和为0,那么若干个非负数都必为0.
例如:若,则,,.
四、绝对值的其它重要性质:
(1)任何一个数的绝对值都不小于这个数,也不小于这个数的相反数,即,
(2);;
当时,
当时,
若,则
(3);
(4),
对于,等号当且仅当、同号或、中至少有一个时,等号成立;
对于,等号当且仅当、异号或、中至少有一个时,等号成立.
知识点六、有理数的四则运算
考点1.有理数的加法
1.有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加.
(2)异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
(3)互为相反的两数相加的0(若a、b互为相反数,则a+b=0).
(4)一个数同0相加,仍得这个数.
2. 有理数的加法运算律:
(1)加法交换律:两个数相加,交换加数的位置,和不变.a+b=b+a
(2)加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
a+b+c=a+(b+c)=b+(a+c)
考点2.有理数的减法
有理数的减法法则:减去一个数,等于加这个数的相反数.a-b=a+(-b).
考点3.有理数的乘法
1.有理数的乘法法则:
(1)两数相乘,同号得正,异号得负,并把绝对值相乘.
(2)任何数与0相乘都得0.
2.有理数的倒数:乘积为1的两个数互为倒数.
3.多个有理数相乘:
(1)几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.
(2)几个有理数相乘,如果其中有一个因数为0,那么积为0.
4.有理数的乘法运算律:
(1)乘法交换律:两个数相乘,交换因数的位置,积不变.
(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.
(3)分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
总结:奇负偶正,先把带分数化成假分数再乘;
分配律、结合律、交换律的灵活应用.
考点4.有理数的除法
有理数的除法法则:
1.除以一个不等于0的数,等于乘这个数的 倒数.
2.两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
除法易错点:①除法没有分配律;
②“单÷多”形式问题两种解法: (1)先将括号里面通分运算出结果,然后按顺序进行计算
(
(2)先计算原式的倒数,求解之后再取倒数即为原式的结果
)
考点5.有理数的乘除混合运算
1.一般将除法转化为乘法;
2.确定积的符号;
3.最后求出结果.
知识点六、有理数的乘方
1.乘方的定义:
求n 个相同因数的积的运算,叫做乘方, 乘方的结果叫做幂.在an中,a 叫
做底数,n 叫做指数.
2.注意:(1)一个数可以看做是这个数本身的一次方,指数1通常省略不写.
(2)因为an就是n个a相乘,所以可以利用乘法运算计算乘方运算.
3.乘方运算的符号法则:
(1)负数的奇次幂是负数,负数的偶次幂的正数.
(2)正数的任何次幂都是正数.
(3)0的任何正整数次幂都是0.
几个常见的易错点:
; ; ; ;
(注意:考试当中一定要注意有无括号,指数的位置)
知识点七、有理数的混合运算
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号,中括号,大括号依次进行.
知识点八、科学计数法、近似数和有效数字
一、科学计数法:
1.定义:把一个大于10的数表示成 的形式(其中a是整数位只有一位的数,n是原数的整数位减1.即1≤|a|<10,n是正整数),这种计数方法叫做科学记数法.(对于小于-10的数也可以类似的表示)
例如:就是科学记数法表示数的形式.
也是科学记数法表示数的形式.
2.注意:(1)用科学计数法只改变数的形式,不改变数的大小.
(2)当把一个用科学计数法 表示的数还原为原数时,只需将小数点向右移动n位(不足的数位用0补齐),并把10n去掉.
二、准确数与近似数
1.准确数:确切地反应了实际的数是一个准确数.
2.近似数:与实际数接近,但有差别的数是一个近似数.
3.近似数的精确度:一个数只是接近实际数,但与实际数还有差别,它是一个近似数。 近似数与准确数的接近程度,可以用精确度表示.一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位.
4.近似数的精确度的表示方法:
①用数位表示:如精确到千位或千分位
②用小数点表示:如精确到0.1或0.01等
③对带有单位的数用单位表示:如精确到千克、米等.
5.注意:万,亿.
三、题型归纳,方法技巧总结
题型一、用正、负数表示具有相反意义的量 1.此类题型解题的关键是弄清楚各问题的“基准”. 对于有基准的问题,要建立表示相反意义的正、负数与实际问题中的相关量之间的关系,从而解决问题.同时,注意0是正数与负数的分界,但并不是所有的分界都是0.
2.在实际生产、生活中,常用“±”表示某个量的允许值的范围,一般约定“+”表示“多出”或“超过”,“—”表示“少于”或“不够”.如用“a±x”表示某个量的范围,其中a表示标准数量,±x表示允许在标准数量上变动的范围.
例题1.用正负数表示具有相反意义的量.
(1)如果零上8 ℃记为+8 ℃,那么-9 ℃表示的意义是_______________ ___;
(2)如果下降了10m记为-10米,那么上升6m记为_ _____________________;
(3)如果前进25km记为+25km,那么后退8km记为___ _________________;
(4)淘淘的妈妈开的超市,今天营利为500元,记作+500元,那么昨天亏损40元记作_______.
【解析】
(1)基准是0℃,零上记为正,零下记为负;
(2)基准是水位不升也不降,下降记为负,上升记为正;
(3)基准是原地不动,前进记为正,后退记为负;
(4)基准是不亏也不赚,盈利记为正,亏损记为负.
【答案】(1)零下9 ℃; (2)+6m;(3)-8km;(4)-40元.
例题2.一袋面粉的质量标识为“25±0.25千克”,则下列面粉中合格的有( )
A.24.70千克 B.25.30千克 C.25.51千克 D.24.80千克
【解析】 “25±0.25千克”的含义是这袋面粉的质量在(25-0.25)千克与(25+0.25)千克之间,即24.75—25.25千克.只要面粉的质量在24.75—25.25千克之间就是合格产品.
【答案】D.
题型二、有理数的大小比较 1.代数法:负数<0<正数. 2.数轴法:数轴上右边的数比左边的数大. 3.绝对值法:对于两个负数,绝对值大的反而小. 4.作差法:,,. 5.作商法:若,,, ,. 6.取倒法:分子一样,通过比较分母从而判定两数的大小. 7.特殊值法:给题目中的字母一个特定的值,然后代入求值,进而比较大小.
例题3.实数在数轴上的对应点如图所示,试比较的大小
【解析】数轴法,作差法,倒数法.根据在数轴上的位置可知,,所以.
【答案】.
例题4.在数轴上表示下列各数,再按大小顺序用“<”号连接起来.
,,,,,,,
【解析】⑴先画出数轴,在数轴上方标注所求数(如图下所示),根据数轴上的大小顺序,按从左到右依次用“<”号连接起来.
即:
【答案】.
例题5.实数在数轴上的对应点如图,试比较的大小.
【解析】根据在数轴上的位置可知,,且的绝对值比的绝对值大,由数轴,作差法得.
【答案】
题型三、数轴的应用 1.数轴上点的移动问题: 可以转化为有理数的加减运算,当初始点未知时,只需要设元解简单方程即可.
2.整点覆盖问题: 线段长为个单位长度,当线段端点在数轴的整数位置覆盖点最多为,当无线段端点在在数轴整点时覆盖点最少.
3.确定原点问题: 将所有点所对应的数用同一个未知数的代数式表示.
4.数轴上两点间的距离为两点对应数的差的绝对值,注意数轴上到已知点距离为定值的点有两个,这个易错点,做题时应当特别小心.
5.数轴上线段定值问题: 数轴上常常会出现动点运动过程中产生定线段或线段和差为定值,这类问题一般通过表示出线段的表达式代入计算即可证明.
6.数轴的折叠问题: 数轴折叠过程中要搞清楚,两对应点与折痕处点的基本规律,即折痕对应点为中点,若两对应点分别记为m、n(m>n),中点记为x, 则:m-x=x-n,所以
7.数轴找规律问题:图形(圆、正方形、等边三角形)在旋转的过程中,根据图形周长有几个单位长度,每旋转一周即循环一次,即可找出对应的规律.
8.数轴上的动点运动问题:这类问题考查了规律型:认真观察、仔细思考,找出点表示的数的变化规律是解题关键.
题型四、绝对值的化简求值
1.条件型绝对值化简
例题6. 已知,化简.
【解析】因为,所以,原式.
【答案】.
2.绝对值零点分段化简
(1)零点的定义:当时,,此时是的零点值.
(2)零点分段讨论的一般步骤:
找零点、分区间、定符号、去绝对值符号.
即先令各绝对值式子为零,求得若干个绝对值为零的点,在数轴上把这些点标出来,这些点把数轴分成若干部分,再在各部分内化简求值.
例题7.化简:(1);(2)
【解析】绝对值零点分段化简,分类讨论.
【答案】(1)原式.(2)原式.
3.分式型绝对值化简:
由绝对值的定义及性质化简:若,则;若,则.
例题8.求下列代数式的值:
(1) _;(2) ;
(3) _____;(4) _____ .
(5) ____ ____;(6) _________ .
【解析】由,则;若,则进行分类讨论化简.
【答案】
(1)、.(2)、.
(3)、、.(4)、、.
(5)原式,将换元本质就与(2)完全相同,
∴原式=、.
(6)原式将、换元本质就与(3)完全相同.∴原式=、、.
题型五、绝对值的实际应用
1.绝对值的几何意义:
(1)|a|的几何意义是:数轴上表示a的点到原点的距离;
(2)|a-b|的几何意义是:数轴上表示数a、b的两点的距离.
例题9.下面材料:已知点A、B在数轴上分别表示有理数、,A、B两点之间的距离表示为.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,
当A、B两点都不在原点时:
(1) 如图2,点A、B都在原点的右边,
(2) 如图3,点A、B都在原点的左边,
(3) 如图4,点A、B在原点的两边,
综上,数轴上A、B两点的距离
回答下列问题:
(1) 数轴上表示-2和-5两点之间的距离是 ;
(2) 数轴上表示和-1的两点A、B之间的距离是,如果,那么为 ;
(3) 当代数式取最小值时,相应的x的取值范围是 .
【解析】由绝对值的几何意义可得.
【答案】(1) 3 ; (2) 1或 ; (3)
2.绝对值之和定值、最值的探讨:
设是常数(是大于的整数),且,是任意实数,求的最小值的一般方法.
根据题意,结合数轴,不难得到:
⑴当为奇数时,取“中间点”:即当(为正整数)时,点应取在 点处,原式的值最小,最小值为
⑵当为偶数时,取“中间段”:即n=(是正整数)时,应取点和点之间的任意位置,原式的值最小,最小值为.
例题10.小红和小明在研究绝对值的问题时,碰到了下面的问题:
“当式子取最小值时,相应的x的取值范围是 ,最小值是 ”.
小红说:“如果去掉绝对值问题就变得简单了。”小明说:“利用数轴可以解决这个问题。”他们把数轴分为三段:,和,经研究发现,当时,值最小为3.
请你根据他们的解题解决下面的问题:
(1)当式子取最小值时,相应的x的取值范围是 ,最小值是 .
(2)已知,求相应的x的取值范围及的最大值。写出解答过程。
【解析】(1),8 ;(2)当时,.
题型六、有理数的速算和巧算
“归”:将同类数(如正数或负数)归类计算.
“消”:将相加得0的数(如互为相反数的数)对消.
“凑”将相加可得整数的数凑整,
“合”:将不同类数(如分母相同或易于通分的数)分别组合.
“分”:将一个数分解成几个数之和的形式,或分解为它的因数相乘的形式.
“化”:将小数与分数或乘法与除法相互转化.
“变”:利用运算定律把运算顺序改变,从而简化计算.
“约”:将互为倒数的数或有因数和倍数关系的数约简.
“逆”:正难则反,逆用运算律以简化运算.
“观”:根据0和1在运算中的特性,注意观察算式特征,可收到事半功倍的效果.
裂项相消:注意观察分母上相乘的两数之差与分子是否相同。若相同,直接裂项;若不相同,需要先在整体前面乘上相对应的分数.
例如:
例题10.速算巧算.
(1).
(2)
(3)
(4)
(5)
(6)
【答案】(1)
(2)原式=
(3)原式=
(4)原式
(5)原式=
(6)原式
