高中数学人教A版2019必修第二册 6.2.1 《向量的减法运算》名师课件(共30张PPT)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 6.2.1 《向量的减法运算》名师课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 21:15:47 | ||
图片预览











文档简介
(共30张PPT)
复习引入
1.向量加法的三角形法则
首尾相连,起点指向终点
起点相同,对角为和
r
r
r
r
.
a
b
b
a
+
=
+
:
.
向量加法的交换律
3
r
r
r
r
r
r
)
(
)
(
c
b
a
c
b
a
+
+
=
+
+
:
.
向量加法的结合律
4
2.向量加法的平行四边形法则
向量的减法运算
学习目标
学 习 目 标 核心素养
通过实例理解向量减法运算的运算法则及实际背景. 数学抽象
理解向量减法运算的几何意义并会作图,加深对向量两要素的理解. 直观想象
体会数形结合思想在向量中的实际运用. 直观想象
教材要点 学科素养 学考 高考 考法指津 高考考向
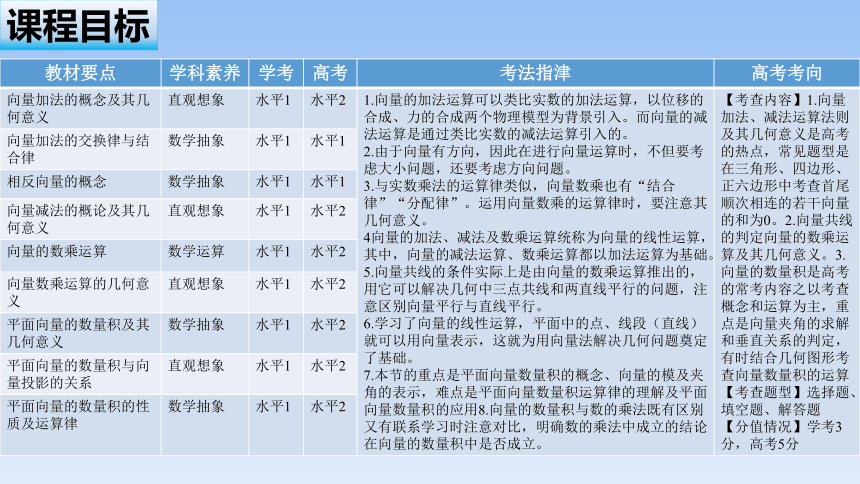
向量加法的概念及其几何意义 直观想象 水平1 水平2 1.向量的加法运算可以类比实数的加法运算,以位移的合成、力的合成两个物理模型为背景引入。而向量的减法运算是通过类比实数的减法运算引入的。 2.由于向量有方向,因此在进行向量运算时,不但要考虑大小问题,还要考虑方向问题。 3.与实数乘法的运算律类似,向量数乘也有“结合律”“分配律”。运用向量数乘的运算律时,要注意其几何意义。 4向量的加法、减法及数乘运算统称为向量的线性运算,其中,向量的减法运算、数乘运算都以加法运算为基础。 5.向量共线的条件实际上是由向量的数乘运算推出的,用它可以解决几何中三点共线和两直线平行的问题,注意区别向量平行与直线平行。 6.学习了向量的线性运算,平面中的点、线段(直线)就可以用向量表示,这就为用向量法解决几何问题奠定了基础。 7.本节的重点是平面向量数量积的概念、向量的模及夹角的表示,难点是平面向量数量积运算律的理解及平面向量数量积的应用8.向量的数量积与数的乘法既有区别又有联系学习时注意对比,明确数的乘法中成立的结论在向量的数量积中是否成立。 【考查内容】1.向量加法、减法运算法则及其几何意义是高考的热点,常见题型是在三角形、四边形、正六边形中考查首尾顺次相连的若干向量的和为0。2.向量共线的判定向量的数乘运算及其几何意义。3.向量的数量积是高考的常考内容之以考查概念和运算为主,重点是向量夹角的求解和垂直关系的判定,有时结合几何图形考查向量数量积的运算
【考查题型】选择题、填空题、解答题
【分值情况】学考3分,高考5分
向量加法的交换律与结合律 数学抽象 水平1 水平1
相反向量的概念 数学抽象 水平1 水平1
向量减法的概论及其几何意义 直观想象 水平1 水平2
向量的数乘运算 数学运算 水平1 水平2
向量数乘运算的几何意义 直观想象 水平1 水平2
平面向量的数量积及其几何意义 数学抽象 水平1 水平2
平面向量的数量积与向量投影的关系 直观想象 水平1 水平2
平面向量的数量积的性质及运算律 数学抽象 水平1 水平2
课程目标
探究新知
探究
向量是否有减法
如何理解向量的减法
我们知道,减去一个数等于加上这个数的相反数,如:5-1=5+(-1)
向量的减法是否也有类似的法则:
减去一个向量等于加上这个向量的相反向量?
探究新知
一架飞机由北京飞往香港,然后再由香港返回北京,我们把北京记作A点,香港记作B点,那么这架飞机的位移是多少 怎样用向量来表示呢
北京(A点)
香港(B点)
+ =
探究新知
1、相反向量
定义:与长度相等,方向相反的向量,叫做 的相反向量,记作:
结论:
(1)
(2)零向量的相反向量仍是零向量
(4)如果是a,b互为相反的向量,那么
在计算中常用
,
BA
AB
=
-
(3)
探究新知
2、向量减法:
定义:
即:减去一个向量相当于加上这个向量的相反向量
把也叫做与的差,与的差也是一个向量.
探究新知
O
A
B
D
C
探究新知
?
二、向量减法的几何意义
O
A
B
①将两向量平移,使它们有相同的起点.
②连接两向量的终点.
③箭头的方向是指向“被减数”的终点.
“共起点,连终点,指向被减向量”
探究新知
思考
?
(1)如图,如果从的终点到的终点作向量,那么所得向量是什么?
探究新知
(1)
(2)
O
A
B
A
B
O
共线
不共线
探究新知
典例讲解
例2、如图,已知向量不共线,求作向量.
法一:如图①,在平面内任取一点O,作= , = , = ,连接BC,则= .
过点A作ADBC,连接OD,则= ,
所以= + = .
解析
典例讲解
例2、如图,已知向量不共线,求作向量.
法二:如图②,在平面内任取一点O,作= , = ,连接OB,则= ,再作= ,连接CB,则= .
解析
典例讲解
例2、如图,已知向量不共线,求作向量.
法三:如图③,在平面内任取一点O,作= ,= ,连接OB,则= ,再作= ,连接OC,则= .
解析
典例讲解
方法归纳
1、如图,已知向量求作向量.
变式训练
解:在平面内任取一点O,作向量= , = ,则向量- = ,再作向量= ,则向量= - - .
例3、化简下列各式:
(1)(+)+(--);(2) --.
(1)法一:
(+)+(--)= +++=+) ++=+=
法二:
(+)+(--)= ++)+=++= + =
(2)法一:
--=-=
法二:
--=-(=-=
解析
典例讲解
向量减法运算的常用方法
方法归纳
2、化简:(1)-+;(2) ++--.
(2) ++--
=+++ +=++++
=++=++=
变式训练
解:(1)法一:.
法二:
例4、如图所示,四边形ACDE是平行四边形,点B是该平行四边形外一点,且= , = , = ,试用向量表示向量, , .
因为四边形ACDE是平行四边形,
所以== ,=-= - ,
故=+= - + .
本例中的条件“点B是该平行四边形外一点”若换为“点B是该平行四边形内一点”,其他条件不变,其结论又如何呢?
因为四边形ACDE是平行四边形,
所以==,=-=-,
故=+= -+.
典例讲解
解析
变式训练
方法归纳
(1)搞清楚图形中的相等向量、相反向量、共线向量以及构成三角形三向量之间的关系,确定已知向量与被表示向量的转化渠道.
(2)注意综合应用向量加法、减法的几何意义以及向量加法的结合律、交换律来分析解决问题.
(3)注意在封闭图形中利用向量加法的多边形法则.
例如,在四边形ABCD中,.
用已知向量表示其他向量的三个关注点
3、如图,O为平行四边形ABCD内一点,=, =,=,则=________.
变式训练
解析:因为,所以,所以.
1.向量减法的实质是向量加法的逆运算.利用相反向量的定义,-=就可以把减法转化为加法.即:减去一个向量等于加上这个向量的相反向量,即= +().
2.在用三角形法则作向量减法时,要注意“差向量连接两向量的终点,箭头指向被减向量”.解题时要结合图形,准确判断,防止混淆.
3.以平行四边形ABCD的两邻边AB、AD分别表示向量= , = ,则两条对角线表示的向量为= + , = - , = - ,这一结论在以后应用非常广泛,应该加强理解并记住.
素养提炼
当堂练习
1.在 ABCD中, 等于( )
2.在 ABCD中,下列结论错误的是( )
3.在△ABC中, ( )
B. C. D.
4.在边长为1的正三角形ABC中, 的值为( )
A.1 B.2
5.若的取值范围是( )
A.[4,7] B.(4,7)
C.[4,10] D.(4,10)
A
C
D
归纳小结
向量的减法
几何意义
相反向量
定义
(一)知识
1.理解相反向量的概念
2. 理解向量减法的定义
3. 正确熟练地掌握向量减法的三角形法则
(二)思想方法
1.类比
2.数形结合
归纳小结
作 业
课本12~13页 练习:1、2
复习引入
1.向量加法的三角形法则
首尾相连,起点指向终点
起点相同,对角为和
r
r
r
r
.
a
b
b
a
+
=
+
:
.
向量加法的交换律
3
r
r
r
r
r
r
)
(
)
(
c
b
a
c
b
a
+
+
=
+
+
:
.
向量加法的结合律
4
2.向量加法的平行四边形法则
向量的减法运算
学习目标
学 习 目 标 核心素养
通过实例理解向量减法运算的运算法则及实际背景. 数学抽象
理解向量减法运算的几何意义并会作图,加深对向量两要素的理解. 直观想象
体会数形结合思想在向量中的实际运用. 直观想象
教材要点 学科素养 学考 高考 考法指津 高考考向
向量加法的概念及其几何意义 直观想象 水平1 水平2 1.向量的加法运算可以类比实数的加法运算,以位移的合成、力的合成两个物理模型为背景引入。而向量的减法运算是通过类比实数的减法运算引入的。 2.由于向量有方向,因此在进行向量运算时,不但要考虑大小问题,还要考虑方向问题。 3.与实数乘法的运算律类似,向量数乘也有“结合律”“分配律”。运用向量数乘的运算律时,要注意其几何意义。 4向量的加法、减法及数乘运算统称为向量的线性运算,其中,向量的减法运算、数乘运算都以加法运算为基础。 5.向量共线的条件实际上是由向量的数乘运算推出的,用它可以解决几何中三点共线和两直线平行的问题,注意区别向量平行与直线平行。 6.学习了向量的线性运算,平面中的点、线段(直线)就可以用向量表示,这就为用向量法解决几何问题奠定了基础。 7.本节的重点是平面向量数量积的概念、向量的模及夹角的表示,难点是平面向量数量积运算律的理解及平面向量数量积的应用8.向量的数量积与数的乘法既有区别又有联系学习时注意对比,明确数的乘法中成立的结论在向量的数量积中是否成立。 【考查内容】1.向量加法、减法运算法则及其几何意义是高考的热点,常见题型是在三角形、四边形、正六边形中考查首尾顺次相连的若干向量的和为0。2.向量共线的判定向量的数乘运算及其几何意义。3.向量的数量积是高考的常考内容之以考查概念和运算为主,重点是向量夹角的求解和垂直关系的判定,有时结合几何图形考查向量数量积的运算
【考查题型】选择题、填空题、解答题
【分值情况】学考3分,高考5分
向量加法的交换律与结合律 数学抽象 水平1 水平1
相反向量的概念 数学抽象 水平1 水平1
向量减法的概论及其几何意义 直观想象 水平1 水平2
向量的数乘运算 数学运算 水平1 水平2
向量数乘运算的几何意义 直观想象 水平1 水平2
平面向量的数量积及其几何意义 数学抽象 水平1 水平2
平面向量的数量积与向量投影的关系 直观想象 水平1 水平2
平面向量的数量积的性质及运算律 数学抽象 水平1 水平2
课程目标
探究新知
探究
向量是否有减法
如何理解向量的减法
我们知道,减去一个数等于加上这个数的相反数,如:5-1=5+(-1)
向量的减法是否也有类似的法则:
减去一个向量等于加上这个向量的相反向量?
探究新知
一架飞机由北京飞往香港,然后再由香港返回北京,我们把北京记作A点,香港记作B点,那么这架飞机的位移是多少 怎样用向量来表示呢
北京(A点)
香港(B点)
+ =
探究新知
1、相反向量
定义:与长度相等,方向相反的向量,叫做 的相反向量,记作:
结论:
(1)
(2)零向量的相反向量仍是零向量
(4)如果是a,b互为相反的向量,那么
在计算中常用
,
BA
AB
=
-
(3)
探究新知
2、向量减法:
定义:
即:减去一个向量相当于加上这个向量的相反向量
把也叫做与的差,与的差也是一个向量.
探究新知
O
A
B
D
C
探究新知
?
二、向量减法的几何意义
O
A
B
①将两向量平移,使它们有相同的起点.
②连接两向量的终点.
③箭头的方向是指向“被减数”的终点.
“共起点,连终点,指向被减向量”
探究新知
思考
?
(1)如图,如果从的终点到的终点作向量,那么所得向量是什么?
探究新知
(1)
(2)
O
A
B
A
B
O
共线
不共线
探究新知
典例讲解
例2、如图,已知向量不共线,求作向量.
法一:如图①,在平面内任取一点O,作= , = , = ,连接BC,则= .
过点A作ADBC,连接OD,则= ,
所以= + = .
解析
典例讲解
例2、如图,已知向量不共线,求作向量.
法二:如图②,在平面内任取一点O,作= , = ,连接OB,则= ,再作= ,连接CB,则= .
解析
典例讲解
例2、如图,已知向量不共线,求作向量.
法三:如图③,在平面内任取一点O,作= ,= ,连接OB,则= ,再作= ,连接OC,则= .
解析
典例讲解
方法归纳
1、如图,已知向量求作向量.
变式训练
解:在平面内任取一点O,作向量= , = ,则向量- = ,再作向量= ,则向量= - - .
例3、化简下列各式:
(1)(+)+(--);(2) --.
(1)法一:
(+)+(--)= +++=+) ++=+=
法二:
(+)+(--)= ++)+=++= + =
(2)法一:
--=-=
法二:
--=-(=-=
解析
典例讲解
向量减法运算的常用方法
方法归纳
2、化简:(1)-+;(2) ++--.
(2) ++--
=+++ +=++++
=++=++=
变式训练
解:(1)法一:.
法二:
例4、如图所示,四边形ACDE是平行四边形,点B是该平行四边形外一点,且= , = , = ,试用向量表示向量, , .
因为四边形ACDE是平行四边形,
所以== ,=-= - ,
故=+= - + .
本例中的条件“点B是该平行四边形外一点”若换为“点B是该平行四边形内一点”,其他条件不变,其结论又如何呢?
因为四边形ACDE是平行四边形,
所以==,=-=-,
故=+= -+.
典例讲解
解析
变式训练
方法归纳
(1)搞清楚图形中的相等向量、相反向量、共线向量以及构成三角形三向量之间的关系,确定已知向量与被表示向量的转化渠道.
(2)注意综合应用向量加法、减法的几何意义以及向量加法的结合律、交换律来分析解决问题.
(3)注意在封闭图形中利用向量加法的多边形法则.
例如,在四边形ABCD中,.
用已知向量表示其他向量的三个关注点
3、如图,O为平行四边形ABCD内一点,=, =,=,则=________.
变式训练
解析:因为,所以,所以.
1.向量减法的实质是向量加法的逆运算.利用相反向量的定义,-=就可以把减法转化为加法.即:减去一个向量等于加上这个向量的相反向量,即= +().
2.在用三角形法则作向量减法时,要注意“差向量连接两向量的终点,箭头指向被减向量”.解题时要结合图形,准确判断,防止混淆.
3.以平行四边形ABCD的两邻边AB、AD分别表示向量= , = ,则两条对角线表示的向量为= + , = - , = - ,这一结论在以后应用非常广泛,应该加强理解并记住.
素养提炼
当堂练习
1.在 ABCD中, 等于( )
2.在 ABCD中,下列结论错误的是( )
3.在△ABC中, ( )
B. C. D.
4.在边长为1的正三角形ABC中, 的值为( )
A.1 B.2
5.若的取值范围是( )
A.[4,7] B.(4,7)
C.[4,10] D.(4,10)
A
C
D
归纳小结
向量的减法
几何意义
相反向量
定义
(一)知识
1.理解相反向量的概念
2. 理解向量减法的定义
3. 正确熟练地掌握向量减法的三角形法则
(二)思想方法
1.类比
2.数形结合
归纳小结
作 业
课本12~13页 练习:1、2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
