高中数学人教A版2019必修第二册 6.2.2《向量的数量积》名师课件(共34张PPT)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 6.2.2《向量的数量积》名师课件(共34张PPT) | 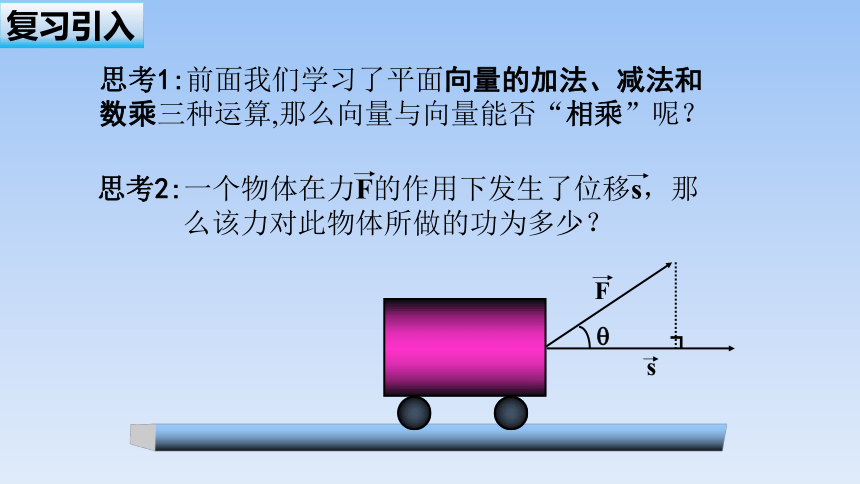 | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 21:17:11 | ||
图片预览










文档简介
(共34张PPT)
思考1:前面我们学面向量的加法、减法和数乘三种运算,那么向量与向量能否“相乘”呢?
思考2:一个物体在力F的作用下发生了位移s,那么该力对此物体所做的功为多少?
F
s
┓
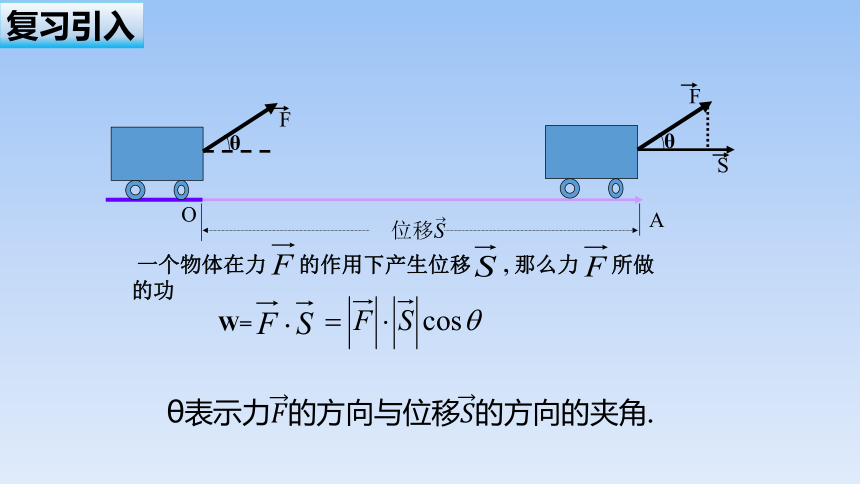
复习引入
位移S
O
A
一个物体在力 的作用下产生位移 , 那么力 所做的功
θ表示力的方向与位移的方向的夹角.
θ
F
F
θ
S
W=
复习引入
我们将功的运算类比到两个向量的一种运算,得到向量“数量积”的概念.
这就是本节课所要学面向量的数量积
|
|
b
|
|
a
=
·
b
a
复习引入
人教A版同步教材名师课件
向量的数量积
学习目标
学 习 目 标 核心素养
掌握向量的数量积及其几何意义. 数学抽象
掌握向量数量积的相关性质及其运算律. 逻辑推理
利用向量的数量积解决相关问题. 直观想象
一、平面向量数量积的定义:
已知两个非零向量和,它们的夹角为 ,我们把数量 叫做与的数量积 (或内积),记作.
规定:零向量与任意向量的数量积为0.
探究新知
注意:
(1) 两个向量的数量积是一个实数,不是向量.
(2)两个向量的数量积称为内积,写成 .
探究新知
注意:
(3) 向量的数量积和实数与向量的积(数乘)不是一回事.
数量积 的结果是一个数量(实数);
实数与向量的积(数乘)还是一个向量.
探究新知
两个非零向量和,作,则 叫做向量和 的夹角.
与 反向
O
A
B
O
A
与 同向
O
A
B
B
记作
与 垂直,
O
A
B
注意:在两向量的夹角定义中,两向量必须是共同起点的
二、两个向量的夹角
探究新知
向量的数量积是一个数量,那么它何时为正,何时为负,何时为零?
探究新知
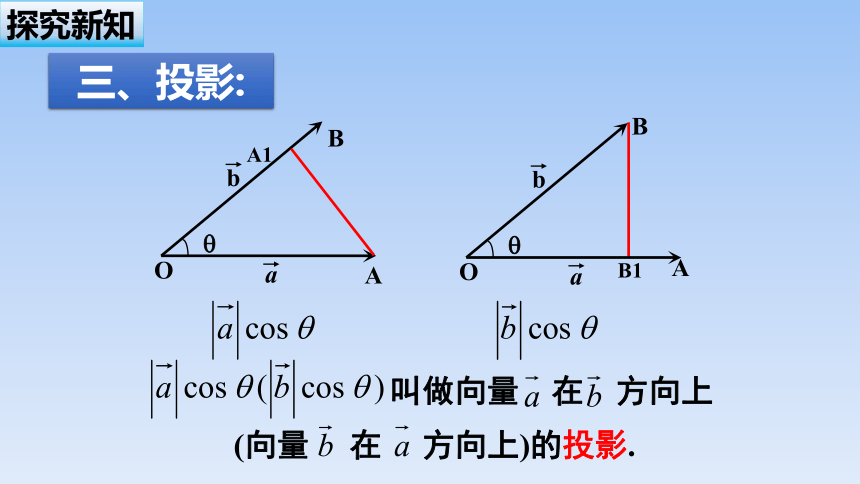
三、投影:
B1
O
A
B
b
a
A1
O
A
B
b
a
叫做向量 在 方向上(向量 在 方向上)的投影.
探究新知
向量在向量上的投影是数量,不是向量,什么时候为正,什么时候为负?
O
A
B
O
A
B
B
O
A
O
A
B
O
A
B
探究新知
四、平面向量数量积的几何意义:
探究新知
平面向量数量积的运算性质
思考1:设与都是非零向量,若⊥,则·等于多少?反之成立吗?
⊥ ·=0
思考2:当与同向时,·等于什么?当与反向时,·等于什么?特别地, · 等于什么?
当与同向时, ·=︱︱︱︱;
当与反向时,·=-︱︱︱ ︱;
·=2=︱︱2或︱︱=.
探究新知
思考3:︱·︱与︱︱︱ ︱的大小关系如何?为什么?
︱·︱ ≤ ︱︱︱︱
思考4: ·与是什么关系?为什么?
·=
思考5:对于实数λ,(λ )· 有意义吗?它可以转化为哪些运算?
(λ )· =λ(·)= ·(λ )
探究新知
思考6:对于向量,()· 有意义吗?它与·+·相等吗?为什么?
A1
B1
A
B
O
C
θ
θ1
θ2
思考7:对于非零向量,,()· 有意义吗?(·)·与·(·)相等吗?为什么?
(·)·≠ ·(·)
探究新知
思考8:对于非零向量,若·= ·,那么=吗?
思考9:对于向量,等式(+)2=2+2·+ 2和(+)(-)=2-2是否成立?为什么?
探究新知
例1、(1)已知两个单位向量的夹角为,若向量=-2=3+4,求·.
(2)设正三角形ABC的边长为,=, =, =,求·+·+·.
(1)由题设知||=||=1且·=,
所以·=(-2)·(3+4)=3-2·-8=3-2×-8=-6.
因为||=||=||=,且与与与的夹角均为120°,
(2)如图,
所以·+·+·=××cos 120°=-3.
典例讲解
解析
(1)求两个向量的数量积,首先确定两个向量的模及向量的夹角,其中准确求出两向量的夹角是求数量积的关键.
(2)根据数量积的运算律,向量的加、减与数量积的混合运算类似于多项式的乘法运算.
向量数量积的求法
方法归纳
1、(1)已知两个单位向量的夹角为60°, = +(1-).若·=0,则=______.
(2)如图,在 ABCD中,| |=4,| |=3,∠DAB=60°,求:① · ;② · ;③ · .
变式训练
解:(1)因为·=0 ,所以·[t+(1-t)]=0,即,又因为, 的夹角为60°,所以,所以2.故填2.
(2)①因为 //,且方向相同,所以的夹角是0°,
所以·| |·| |
②因为 //,且方向相反,所以的夹角是180°,
所以| |·| |.
③因为 的夹角是60°,所以的夹角是120° ,
所以| |·| |.
例2、设向量满足=,()⊥,||=1,则||=_____.
因为=,所以=-().
因为()⊥,所以·()=0,
所以-()·()=0,
所以2-2=0,所以||=||=1.
若本例增加条件“⊥”,求||.
由已知可得=-() ,而()⊥,
有-()·()=0 ,所以2-2=0 ,
又||=1 ,得||=1 ,而⊥,
所以2=[-()]2=2+2+2=2,即||=.
典例讲解
解析
变式训练
方法归纳
(1)求模问题一般转化为求模的平方,与向量数量积联系,并灵活应用2=||2,勿忘记开方.
(2)·=2 =||2或||=,可以实现实数运算与向量运算的相互转化.
求向量的模的常见思路及方法
2、(1)已知平面向量与的夹角为60°,||=2,||=1,则|+2|=( )
A. B.2 C.4 D.12
(2)已知向量满足||=2,||=3,|+|=4,则|-|=________.
(1)|+2|==
= = =2.
解析
B
(2)因为|+|=4 ,所以| +|2=42,所以=16.①
因为||=2,||=3 ,所以=||2=4,=||2=9,
代入①式得4+2+9=16,得2=3.
又因为(-)2= =4-3+9=10,所以|-|=.
变式训练
例3、(1)已知非零向量,满足||=4||,且⊥(2a+),则与的夹角为( )
A. B. C. D.
(2)已知非零向量,满足||=1,且()·()=.
①求|| ;②当=时,求向量与的夹角θ的值.
(1) 设,的夹角为θ,因为 ⊥(2a+) ,所以· (2a+) =0,
解析
所以 2||2+=0,即2||2+||||cos θ=0.
因为||=4||,所以 2||2+4||2cos θ=0,
所以 cos θ=-,所以θ=.
C
(2)①因为()·()=,即=,
所以||2= ||2-=1-=,故||=.
②因为cos θ==,又0°≤θ≤180°,故θ=45°.
典例讲解
(2)注意事项:在个别含有||,||与·的等量关系式中,常利用消元思想计算cos θ的值.
求向量夹角的基本步骤及注意事项
(1)步骤:
方法归纳
3、已知||=2||=2,且在方向上的投影为-1.
(1)求与的夹角θ;(2)求(-2)·;
(3)当λ为何值时,向量λ+与向量-3互相垂直?
解:(1)因为||=2||=2 ,所以|| =2, || =1.
又在方向上的投影为||cos θ=-1,
所以=||||cos θ=-1,所以cos θ=-,所以θ=.
(2)(-2)·=-22=-1-2=-3.
(3)因为λ+与-3互相垂直,所以(λ+)·(-3)=λ2-3λ+·-32=0,所以4λ+3λ-1-3=7λ-4=0,所以λ=.
变式训练
(1) ·等于||与在方向上的投影的乘积,也等于||与在方向上的投影的乘积.其中在方向上的投影与在方向上的投影是不同的.
(2) 在方向上的投影为||cos θ(θ是与的夹角),也可以写成.
(3)投影是一个数量,不是向量,其值可为正,可为负,也可为零.
素养提炼
1.对投影的三点诠释
素养提炼
2.向量的数量积与实数乘积运算性质的比较
当堂练习
1.若向量,满足,则等于( )
2.已知,设是与方向相同的单位向量,则向量在向量上的投影向量为( )
A.4 B.-4 C.2 D.-2
3.如果向量,满足且与的夹角为,那么等于( )
D.3
4.在△ABC中, ,则三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
5.已知,与方向相同的单位向量为,向量在向量上的投影向量是等于( )
A.3 C.2
B
D
C
当堂练习
6.若非零向量,满足,则与的夹角为( )
7.若向量与的夹角为60°,,则向量的模为( )
A.2 B.4 C.6 D.12
8.若向量,满足,则等于( )
A.3 C.10
9.已知向量,的夹角为120°,同向,则的最小值为( )
A.1
C
C
D
归纳小结
向量的数量积
向量数量积的性质
向量的数量积的定义
投影向量
数量积运算的运算律
1.向量的数量积是一种向量的乘法运算,它与向量的加法、减法、数乘运算一样,也有明显的物理背景和几何意义,同时还有一系列的运算性质,但与向量的线性运算不同的是,数量积的运算结果是数量而不是向量.
归纳小结
2.实数的运算性质与向量的运算性质不完全一致,应用时不要似是而非.
3. 利用︱︱= 可以求向量的模,在字符运算中是一种常用方法.
4.利用向量的数量积可以解决有关平行、垂直、夹角、距离、不等式等问题,它是一个工具性知识点,具有很强的功能作用.
归纳小结
作 业
P20 练习:1、2、3;
P22 练习:1、2、3.
思考1:前面我们学面向量的加法、减法和数乘三种运算,那么向量与向量能否“相乘”呢?
思考2:一个物体在力F的作用下发生了位移s,那么该力对此物体所做的功为多少?
F
s
┓
复习引入
位移S
O
A
一个物体在力 的作用下产生位移 , 那么力 所做的功
θ表示力的方向与位移的方向的夹角.
θ
F
F
θ
S
W=
复习引入
我们将功的运算类比到两个向量的一种运算,得到向量“数量积”的概念.
这就是本节课所要学面向量的数量积
|
|
b
|
|
a
=
·
b
a
复习引入
人教A版同步教材名师课件
向量的数量积
学习目标
学 习 目 标 核心素养
掌握向量的数量积及其几何意义. 数学抽象
掌握向量数量积的相关性质及其运算律. 逻辑推理
利用向量的数量积解决相关问题. 直观想象
一、平面向量数量积的定义:
已知两个非零向量和,它们的夹角为 ,我们把数量 叫做与的数量积 (或内积),记作.
规定:零向量与任意向量的数量积为0.
探究新知
注意:
(1) 两个向量的数量积是一个实数,不是向量.
(2)两个向量的数量积称为内积,写成 .
探究新知
注意:
(3) 向量的数量积和实数与向量的积(数乘)不是一回事.
数量积 的结果是一个数量(实数);
实数与向量的积(数乘)还是一个向量.
探究新知
两个非零向量和,作,则 叫做向量和 的夹角.
与 反向
O
A
B
O
A
与 同向
O
A
B
B
记作
与 垂直,
O
A
B
注意:在两向量的夹角定义中,两向量必须是共同起点的
二、两个向量的夹角
探究新知
向量的数量积是一个数量,那么它何时为正,何时为负,何时为零?
探究新知
三、投影:
B1
O
A
B
b
a
A1
O
A
B
b
a
叫做向量 在 方向上(向量 在 方向上)的投影.
探究新知
向量在向量上的投影是数量,不是向量,什么时候为正,什么时候为负?
O
A
B
O
A
B
B
O
A
O
A
B
O
A
B
探究新知
四、平面向量数量积的几何意义:
探究新知
平面向量数量积的运算性质
思考1:设与都是非零向量,若⊥,则·等于多少?反之成立吗?
⊥ ·=0
思考2:当与同向时,·等于什么?当与反向时,·等于什么?特别地, · 等于什么?
当与同向时, ·=︱︱︱︱;
当与反向时,·=-︱︱︱ ︱;
·=2=︱︱2或︱︱=.
探究新知
思考3:︱·︱与︱︱︱ ︱的大小关系如何?为什么?
︱·︱ ≤ ︱︱︱︱
思考4: ·与是什么关系?为什么?
·=
思考5:对于实数λ,(λ )· 有意义吗?它可以转化为哪些运算?
(λ )· =λ(·)= ·(λ )
探究新知
思考6:对于向量,()· 有意义吗?它与·+·相等吗?为什么?
A1
B1
A
B
O
C
θ
θ1
θ2
思考7:对于非零向量,,()· 有意义吗?(·)·与·(·)相等吗?为什么?
(·)·≠ ·(·)
探究新知
思考8:对于非零向量,若·= ·,那么=吗?
思考9:对于向量,等式(+)2=2+2·+ 2和(+)(-)=2-2是否成立?为什么?
探究新知
例1、(1)已知两个单位向量的夹角为,若向量=-2=3+4,求·.
(2)设正三角形ABC的边长为,=, =, =,求·+·+·.
(1)由题设知||=||=1且·=,
所以·=(-2)·(3+4)=3-2·-8=3-2×-8=-6.
因为||=||=||=,且与与与的夹角均为120°,
(2)如图,
所以·+·+·=××cos 120°=-3.
典例讲解
解析
(1)求两个向量的数量积,首先确定两个向量的模及向量的夹角,其中准确求出两向量的夹角是求数量积的关键.
(2)根据数量积的运算律,向量的加、减与数量积的混合运算类似于多项式的乘法运算.
向量数量积的求法
方法归纳
1、(1)已知两个单位向量的夹角为60°, = +(1-).若·=0,则=______.
(2)如图,在 ABCD中,| |=4,| |=3,∠DAB=60°,求:① · ;② · ;③ · .
变式训练
解:(1)因为·=0 ,所以·[t+(1-t)]=0,即,又因为, 的夹角为60°,所以,所以2.故填2.
(2)①因为 //,且方向相同,所以的夹角是0°,
所以·| |·| |
②因为 //,且方向相反,所以的夹角是180°,
所以| |·| |.
③因为 的夹角是60°,所以的夹角是120° ,
所以| |·| |.
例2、设向量满足=,()⊥,||=1,则||=_____.
因为=,所以=-().
因为()⊥,所以·()=0,
所以-()·()=0,
所以2-2=0,所以||=||=1.
若本例增加条件“⊥”,求||.
由已知可得=-() ,而()⊥,
有-()·()=0 ,所以2-2=0 ,
又||=1 ,得||=1 ,而⊥,
所以2=[-()]2=2+2+2=2,即||=.
典例讲解
解析
变式训练
方法归纳
(1)求模问题一般转化为求模的平方,与向量数量积联系,并灵活应用2=||2,勿忘记开方.
(2)·=2 =||2或||=,可以实现实数运算与向量运算的相互转化.
求向量的模的常见思路及方法
2、(1)已知平面向量与的夹角为60°,||=2,||=1,则|+2|=( )
A. B.2 C.4 D.12
(2)已知向量满足||=2,||=3,|+|=4,则|-|=________.
(1)|+2|==
= = =2.
解析
B
(2)因为|+|=4 ,所以| +|2=42,所以=16.①
因为||=2,||=3 ,所以=||2=4,=||2=9,
代入①式得4+2+9=16,得2=3.
又因为(-)2= =4-3+9=10,所以|-|=.
变式训练
例3、(1)已知非零向量,满足||=4||,且⊥(2a+),则与的夹角为( )
A. B. C. D.
(2)已知非零向量,满足||=1,且()·()=.
①求|| ;②当=时,求向量与的夹角θ的值.
(1) 设,的夹角为θ,因为 ⊥(2a+) ,所以· (2a+) =0,
解析
所以 2||2+=0,即2||2+||||cos θ=0.
因为||=4||,所以 2||2+4||2cos θ=0,
所以 cos θ=-,所以θ=.
C
(2)①因为()·()=,即=,
所以||2= ||2-=1-=,故||=.
②因为cos θ==,又0°≤θ≤180°,故θ=45°.
典例讲解
(2)注意事项:在个别含有||,||与·的等量关系式中,常利用消元思想计算cos θ的值.
求向量夹角的基本步骤及注意事项
(1)步骤:
方法归纳
3、已知||=2||=2,且在方向上的投影为-1.
(1)求与的夹角θ;(2)求(-2)·;
(3)当λ为何值时,向量λ+与向量-3互相垂直?
解:(1)因为||=2||=2 ,所以|| =2, || =1.
又在方向上的投影为||cos θ=-1,
所以=||||cos θ=-1,所以cos θ=-,所以θ=.
(2)(-2)·=-22=-1-2=-3.
(3)因为λ+与-3互相垂直,所以(λ+)·(-3)=λ2-3λ+·-32=0,所以4λ+3λ-1-3=7λ-4=0,所以λ=.
变式训练
(1) ·等于||与在方向上的投影的乘积,也等于||与在方向上的投影的乘积.其中在方向上的投影与在方向上的投影是不同的.
(2) 在方向上的投影为||cos θ(θ是与的夹角),也可以写成.
(3)投影是一个数量,不是向量,其值可为正,可为负,也可为零.
素养提炼
1.对投影的三点诠释
素养提炼
2.向量的数量积与实数乘积运算性质的比较
当堂练习
1.若向量,满足,则等于( )
2.已知,设是与方向相同的单位向量,则向量在向量上的投影向量为( )
A.4 B.-4 C.2 D.-2
3.如果向量,满足且与的夹角为,那么等于( )
D.3
4.在△ABC中, ,则三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
5.已知,与方向相同的单位向量为,向量在向量上的投影向量是等于( )
A.3 C.2
B
D
C
当堂练习
6.若非零向量,满足,则与的夹角为( )
7.若向量与的夹角为60°,,则向量的模为( )
A.2 B.4 C.6 D.12
8.若向量,满足,则等于( )
A.3 C.10
9.已知向量,的夹角为120°,同向,则的最小值为( )
A.1
C
C
D
归纳小结
向量的数量积
向量数量积的性质
向量的数量积的定义
投影向量
数量积运算的运算律
1.向量的数量积是一种向量的乘法运算,它与向量的加法、减法、数乘运算一样,也有明显的物理背景和几何意义,同时还有一系列的运算性质,但与向量的线性运算不同的是,数量积的运算结果是数量而不是向量.
归纳小结
2.实数的运算性质与向量的运算性质不完全一致,应用时不要似是而非.
3. 利用︱︱= 可以求向量的模,在字符运算中是一种常用方法.
4.利用向量的数量积可以解决有关平行、垂直、夹角、距离、不等式等问题,它是一个工具性知识点,具有很强的功能作用.
归纳小结
作 业
P20 练习:1、2、3;
P22 练习:1、2、3.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
