高中数学人教A版2019必修第二册 6.2.3向量的数乘运算 课件(共36张PPT)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 6.2.3向量的数乘运算 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 21:20:36 | ||
图片预览











文档简介
(共36张PPT)
6.2.3 向量的数乘运算
一
二
三
一、向量的数乘运算
1.思考
(1)质点从点O出发做匀速直线运动,若经过1 s的位移对应的向量用a表示,那么在同方向上经过3 s的位移所对应的向量是多少
提示3a
(2)已知非零向量a,作出a+a+a和(-a)+(-a)+(-a).
一
二
三
(3)上述两个和向量有什么几何意义
提示类似数的乘法,我们把a+a+a记作3a,即 =3a.显然3a的方向与a的方向相同,3a的长度是a的长度的3倍,即|3a|=3|a|.
同样,把(-a)+(-a)+(-a)记作3(-a).显然3(-a)的方向与a的方向相反,3(-a)的长度是a的长度的3倍,这样,3(-a)=-3a.
一
二
三
2.填空
一
二
三
3.做一做
(1)若|a|=3,|b|= ,则|-2a|= ,|3b|= .
(2)若a与b是相反向量,则5a与-4b的方向 .
一
二
三
二、数乘向量的运算律
1.思考
(1)我们学习过的实数乘法有哪些运算律
提示①乘法交换律:ab=ba;
②乘法结合律:(ab)c=a(bc);
③乘法分配律:a(b+c)=ab+ac.其中a,b,c表示任意实数.
一
二
三
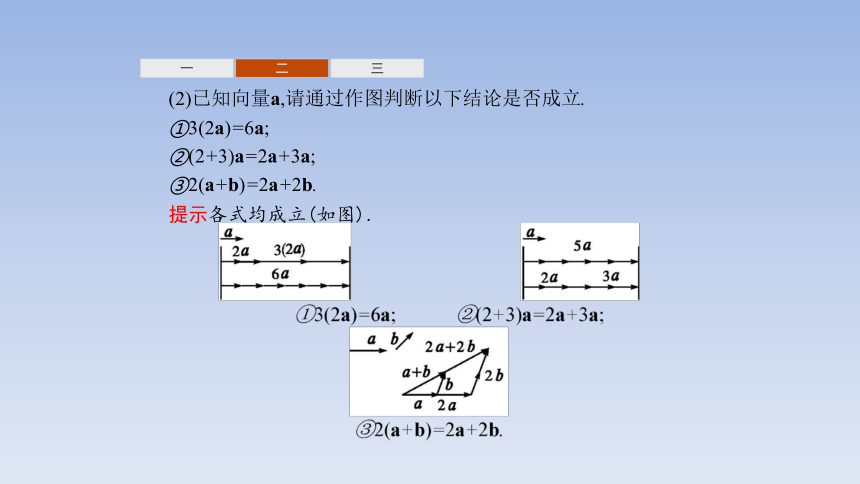
(2)已知向量a,请通过作图判断以下结论是否成立.
①3(2a)=6a;
②(2+3)a=2a+3a;
③2(a+b)=2a+2b.
提示各式均成立(如图).
一
二
三
2.填空
(1)数乘向量的运算律
①λ(μa)=(λμ)a;
②(λ+μ)a=λa+μa;
③λ(a+b)=λa+λb.
特别地,有(-λ)a=-(λa)=λ(-a);λ(a-b)=λa-λb.
(2)向量的加法、减法、数乘运算统称为向量的线性运算.向量线性运算的结果仍是向量.对于任意向量a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1a±μ2b)=λμ1a±λμ2b.
一
二
三
3.做一做
A.2a+3b B.a-3b C.2a-3b D.2a-2b
答案:C
一
二
三
三、共线向量定理
1.思考
(1)数乘向量λa(λ∈R)与原向量a(a≠0)之间有什么关系
提示设b=λa,可知a与b共线.
(2)上述结论反过来如何表述 还成立吗
提示反过来可表述为:如果向量a(a≠0)与b共线,那么存在唯一的λ∈R,使b=λa成立.
这一结论是正确的,证明如下:已知a(a≠0)与b共线,由向量数乘的定义知:
②当b=0时,b=λa(a≠0),此时λ=0.
一
二
三
(3)向量共线定理中为什么要注明“a≠0”
提示如果a=0,则λa=0,当b为非零向量时,a与b共线,但b≠λa,定理不成立;当b=0时,b=λa,但λ可以取任意实数.
2.填空
(1)向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使b=λa.
(2)要证明向量a,b共线,只需证明存在实数λ,使得b=λa即可.
(3)若b=λa(λ∈R),则a与b共线.
一
二
三
3.做一做
(1)若向量e1,e2不共线,则下列各组中,向量a,b共线的有 .(填序号)
①a=2e1,b=-2e1;
②a=e1-e2,b=-2e1+2e2;
④a=e1+e2,b=2e1-2e2.
答案:①②③
解析:①中,a=-b,所以a,b共线;②中,b=-2a,所以a,b共线;③中,a=4b,所以a,b共线;④中,不存在λ∈R,使a=λb,所以a,b不共线.
一
二
三
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①向量λa与a的方向不是相同就是相反.( )
②若向量a和b共线,则必有b=λa.( )
答案:①× ②× ③×
探究一
探究二
探究三
思维辨析
随堂演练
向量的线性运算
例1(1)化简下列各向量表达式:
分析(1)根据向量的线性运算法则求解;(2)运用实数的二元一次方程组的解法求解.
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 向量的线性运算类似于代数多项式的运算,共线向量可以合并,即“合并同类项”“提取公因式”,这里的“同类项”“公因式”指的是向量.运算时要遵循括号内运算优先的原则.
探究一
探究二
探究三
思维辨析
随堂演练
A.2a-b B.2b-a C.b-a D.a-b
(2)已知2a-b=m,a+3b=n,那么a,b用m,n可以表示为a= ,b= .
探究一
探究二
探究三
思维辨析
随堂演练
共线向量定理及其应用
角度1 向量共线的判定
例2判断下列各小题中的向量a,b是否共线(其中e1,e2是两非零不共线向量).
(1)a=5e1,b=-10e1;
(3)a=e1+e2,b=3e1-3e2.
探究一
探究二
探究三
思维辨析
随堂演练
解:(1)∵b=-2a,∴a与b共线.
(3)设a=λb,则e1+e2=λ(3e1-3e2),
∴(1-3λ)e1+(1+3λ)e2=0.
∵e1与e2是两非零不共线向量,
∴1-3λ=0,1+3λ=0.
这样的λ不存在,因此a与b不共线.
反思感悟 向量共线的判定一般是用其判定定理,即a是一个非零向量,若存在唯一一个实数λ,使得b=λa,则向量b与非零向量a共线.解题过程中,需要把两向量用共同的已知向量来表示,进而互相表示,由此判断共线.
探究一
探究二
探究三
思维辨析
随堂演练
角度2 用已知向量表示未知向量
答案:C
反思感悟 用已知向量来表示另外一些所求未知向量是解向量相关问题的基础,除了要利用向量的加、减、数乘运算外,还应充分利用平面几何的一些定理、性质,如三角形的中位线定理,相似三角形对应边成比例等,把未知向量转化为与已知向量有直接关系的向量进行求解.
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
角度3 证明三点共线问题
反思感悟 1.证明三点共线,通常转化为证明由这三点构成的两个向量共线,两个向量共线的充要条件是解决向量共线问题的依据.
2.若A,B,C三点共线,则向量 在同一直线上,因此必定存在实数,使得其中两个向量之间存在线性关系,而向量共线定理是实现线性关系的依据.
探究一
探究二
探究三
思维辨析
随堂演练
(1)求证:A,B,M三点共线;
(2)若点B在线段AM上,求实数λ的取值范围.
探究一
探究二
探究三
思维辨析
随堂演练
角度4 求参问题
答案:A
探究一
探究二
探究三
思维辨析
随堂演练
答案:C
探究一
探究二
探究三
思维辨析
随堂演练
向量线性运算的综合应用
角度1 求解三角形的面积比
答案:D
探究一
探究二
探究三
思维辨析
随堂演练
答案:C
探究一
探究二
探究三
思维辨析
随堂演练
角度2 解决三角形的四心问题
答案:B
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
A.外心 B.重心
C.垂心 D.内心
答案:B
探究一
探究二
探究三
思维辨析
随堂演练
对共线向量的条件理解不清致误
典例已知非零向量e1和e2,试判断3e1+2e2与3e1-2e2是否共线.
错解:若存在实数λ,使3e1+2e2=λ(3e1-2e2),
则3e1+2e2=3λe1-2λe2,即(3-3λ)e1=(-2λ-2)e2,
错解错在什么地方 你能发现吗 怎样避免这类错误呢
提示错解中对向量共线的条件理解不清,只有当e1,e2不共线,且λe1=μe2时,才有λ=μ=0,否则不一定成立.题目条件没有限定e1和e2不共线,因此,上述解法是错误的.
探究一
探究二
探究三
思维辨析
随堂演练
正解:①若向量e1和e2不共线,由错解过程可知3e1+2e2与3e1-2e2不共线.
②若向量e1和e2共线,可设e2=ke1(k∈R),
则3e1+2e2=(3+2k)e1,3e1-2e2=(3-2k)e1,
3+2k与3-2k中至少有一个不为0,不妨设3-2k≠0,
防错有术 本题容易对向量共线的条件理解不清而致误,即没有考虑e1与e2共线的情况.要注意结论“若非零向量e1,e2不共线,且λe1=μe2,则必有λ=μ=0”成立的条件是e1,e2不共线,因此在应用该结论解决相关问题时,务必注意这一条件.
探究一
探究二
探究三
思维辨析
随堂演练
1.设a是非零向量,λ是非零实数,则下列结论正确的是 ( )
A.a与λa的方向相同 B.a与-λa的方向相反
C.a与λ2a的方向相同 D.|λa|=λ|a|
答案:C
解析:因为λ≠0,所以λ2>0,于是向量a与λ2a的方向相同.
2.4(a-b)-3(a+b)-b等于( )
A.a-2b B.a
C.a-6b D.a-8b
答案:D
解析:原式=4a-4b-3a-3b-b=a-8b.
探究一
探究二
探究三
思维辨析
随堂演练
3.下列说法正确的个数为( )
①0·a=0;②0·a=0;③a·0=0;④a·0=0.
A.1 B.2 C.3 D.4
答案:B
解析:本题考查数乘向量运算的理解,由于数乘向量的结果是一个向量而不是一个数,因此本题所给的四种说法中只有②与③的结果是一个向量,因此选B.
探究一
探究二
探究三
思维辨析
随堂演练
5.已知两个非零向量a,b不共线,且ka+3b与2a+kb共线,求实数k的值.
解:因为ka+3b与2a+kb共线,
所以存在实数λ,使ka+3b=λ(2a+kb),
即ka+3b=2λa+λkb,即(k-2λ)a=(λk-3)b.
探究一
探究二
探究三
思维辨析
随堂演练
6.2.3 向量的数乘运算
一
二
三
一、向量的数乘运算
1.思考
(1)质点从点O出发做匀速直线运动,若经过1 s的位移对应的向量用a表示,那么在同方向上经过3 s的位移所对应的向量是多少
提示3a
(2)已知非零向量a,作出a+a+a和(-a)+(-a)+(-a).
一
二
三
(3)上述两个和向量有什么几何意义
提示类似数的乘法,我们把a+a+a记作3a,即 =3a.显然3a的方向与a的方向相同,3a的长度是a的长度的3倍,即|3a|=3|a|.
同样,把(-a)+(-a)+(-a)记作3(-a).显然3(-a)的方向与a的方向相反,3(-a)的长度是a的长度的3倍,这样,3(-a)=-3a.
一
二
三
2.填空
一
二
三
3.做一做
(1)若|a|=3,|b|= ,则|-2a|= ,|3b|= .
(2)若a与b是相反向量,则5a与-4b的方向 .
一
二
三
二、数乘向量的运算律
1.思考
(1)我们学习过的实数乘法有哪些运算律
提示①乘法交换律:ab=ba;
②乘法结合律:(ab)c=a(bc);
③乘法分配律:a(b+c)=ab+ac.其中a,b,c表示任意实数.
一
二
三
(2)已知向量a,请通过作图判断以下结论是否成立.
①3(2a)=6a;
②(2+3)a=2a+3a;
③2(a+b)=2a+2b.
提示各式均成立(如图).
一
二
三
2.填空
(1)数乘向量的运算律
①λ(μa)=(λμ)a;
②(λ+μ)a=λa+μa;
③λ(a+b)=λa+λb.
特别地,有(-λ)a=-(λa)=λ(-a);λ(a-b)=λa-λb.
(2)向量的加法、减法、数乘运算统称为向量的线性运算.向量线性运算的结果仍是向量.对于任意向量a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1a±μ2b)=λμ1a±λμ2b.
一
二
三
3.做一做
A.2a+3b B.a-3b C.2a-3b D.2a-2b
答案:C
一
二
三
三、共线向量定理
1.思考
(1)数乘向量λa(λ∈R)与原向量a(a≠0)之间有什么关系
提示设b=λa,可知a与b共线.
(2)上述结论反过来如何表述 还成立吗
提示反过来可表述为:如果向量a(a≠0)与b共线,那么存在唯一的λ∈R,使b=λa成立.
这一结论是正确的,证明如下:已知a(a≠0)与b共线,由向量数乘的定义知:
②当b=0时,b=λa(a≠0),此时λ=0.
一
二
三
(3)向量共线定理中为什么要注明“a≠0”
提示如果a=0,则λa=0,当b为非零向量时,a与b共线,但b≠λa,定理不成立;当b=0时,b=λa,但λ可以取任意实数.
2.填空
(1)向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使b=λa.
(2)要证明向量a,b共线,只需证明存在实数λ,使得b=λa即可.
(3)若b=λa(λ∈R),则a与b共线.
一
二
三
3.做一做
(1)若向量e1,e2不共线,则下列各组中,向量a,b共线的有 .(填序号)
①a=2e1,b=-2e1;
②a=e1-e2,b=-2e1+2e2;
④a=e1+e2,b=2e1-2e2.
答案:①②③
解析:①中,a=-b,所以a,b共线;②中,b=-2a,所以a,b共线;③中,a=4b,所以a,b共线;④中,不存在λ∈R,使a=λb,所以a,b不共线.
一
二
三
(2)判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
①向量λa与a的方向不是相同就是相反.( )
②若向量a和b共线,则必有b=λa.( )
答案:①× ②× ③×
探究一
探究二
探究三
思维辨析
随堂演练
向量的线性运算
例1(1)化简下列各向量表达式:
分析(1)根据向量的线性运算法则求解;(2)运用实数的二元一次方程组的解法求解.
探究一
探究二
探究三
思维辨析
随堂演练
反思感悟 向量的线性运算类似于代数多项式的运算,共线向量可以合并,即“合并同类项”“提取公因式”,这里的“同类项”“公因式”指的是向量.运算时要遵循括号内运算优先的原则.
探究一
探究二
探究三
思维辨析
随堂演练
A.2a-b B.2b-a C.b-a D.a-b
(2)已知2a-b=m,a+3b=n,那么a,b用m,n可以表示为a= ,b= .
探究一
探究二
探究三
思维辨析
随堂演练
共线向量定理及其应用
角度1 向量共线的判定
例2判断下列各小题中的向量a,b是否共线(其中e1,e2是两非零不共线向量).
(1)a=5e1,b=-10e1;
(3)a=e1+e2,b=3e1-3e2.
探究一
探究二
探究三
思维辨析
随堂演练
解:(1)∵b=-2a,∴a与b共线.
(3)设a=λb,则e1+e2=λ(3e1-3e2),
∴(1-3λ)e1+(1+3λ)e2=0.
∵e1与e2是两非零不共线向量,
∴1-3λ=0,1+3λ=0.
这样的λ不存在,因此a与b不共线.
反思感悟 向量共线的判定一般是用其判定定理,即a是一个非零向量,若存在唯一一个实数λ,使得b=λa,则向量b与非零向量a共线.解题过程中,需要把两向量用共同的已知向量来表示,进而互相表示,由此判断共线.
探究一
探究二
探究三
思维辨析
随堂演练
角度2 用已知向量表示未知向量
答案:C
反思感悟 用已知向量来表示另外一些所求未知向量是解向量相关问题的基础,除了要利用向量的加、减、数乘运算外,还应充分利用平面几何的一些定理、性质,如三角形的中位线定理,相似三角形对应边成比例等,把未知向量转化为与已知向量有直接关系的向量进行求解.
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
角度3 证明三点共线问题
反思感悟 1.证明三点共线,通常转化为证明由这三点构成的两个向量共线,两个向量共线的充要条件是解决向量共线问题的依据.
2.若A,B,C三点共线,则向量 在同一直线上,因此必定存在实数,使得其中两个向量之间存在线性关系,而向量共线定理是实现线性关系的依据.
探究一
探究二
探究三
思维辨析
随堂演练
(1)求证:A,B,M三点共线;
(2)若点B在线段AM上,求实数λ的取值范围.
探究一
探究二
探究三
思维辨析
随堂演练
角度4 求参问题
答案:A
探究一
探究二
探究三
思维辨析
随堂演练
答案:C
探究一
探究二
探究三
思维辨析
随堂演练
向量线性运算的综合应用
角度1 求解三角形的面积比
答案:D
探究一
探究二
探究三
思维辨析
随堂演练
答案:C
探究一
探究二
探究三
思维辨析
随堂演练
角度2 解决三角形的四心问题
答案:B
探究一
探究二
探究三
思维辨析
随堂演练
探究一
探究二
探究三
思维辨析
随堂演练
A.外心 B.重心
C.垂心 D.内心
答案:B
探究一
探究二
探究三
思维辨析
随堂演练
对共线向量的条件理解不清致误
典例已知非零向量e1和e2,试判断3e1+2e2与3e1-2e2是否共线.
错解:若存在实数λ,使3e1+2e2=λ(3e1-2e2),
则3e1+2e2=3λe1-2λe2,即(3-3λ)e1=(-2λ-2)e2,
错解错在什么地方 你能发现吗 怎样避免这类错误呢
提示错解中对向量共线的条件理解不清,只有当e1,e2不共线,且λe1=μe2时,才有λ=μ=0,否则不一定成立.题目条件没有限定e1和e2不共线,因此,上述解法是错误的.
探究一
探究二
探究三
思维辨析
随堂演练
正解:①若向量e1和e2不共线,由错解过程可知3e1+2e2与3e1-2e2不共线.
②若向量e1和e2共线,可设e2=ke1(k∈R),
则3e1+2e2=(3+2k)e1,3e1-2e2=(3-2k)e1,
3+2k与3-2k中至少有一个不为0,不妨设3-2k≠0,
防错有术 本题容易对向量共线的条件理解不清而致误,即没有考虑e1与e2共线的情况.要注意结论“若非零向量e1,e2不共线,且λe1=μe2,则必有λ=μ=0”成立的条件是e1,e2不共线,因此在应用该结论解决相关问题时,务必注意这一条件.
探究一
探究二
探究三
思维辨析
随堂演练
1.设a是非零向量,λ是非零实数,则下列结论正确的是 ( )
A.a与λa的方向相同 B.a与-λa的方向相反
C.a与λ2a的方向相同 D.|λa|=λ|a|
答案:C
解析:因为λ≠0,所以λ2>0,于是向量a与λ2a的方向相同.
2.4(a-b)-3(a+b)-b等于( )
A.a-2b B.a
C.a-6b D.a-8b
答案:D
解析:原式=4a-4b-3a-3b-b=a-8b.
探究一
探究二
探究三
思维辨析
随堂演练
3.下列说法正确的个数为( )
①0·a=0;②0·a=0;③a·0=0;④a·0=0.
A.1 B.2 C.3 D.4
答案:B
解析:本题考查数乘向量运算的理解,由于数乘向量的结果是一个向量而不是一个数,因此本题所给的四种说法中只有②与③的结果是一个向量,因此选B.
探究一
探究二
探究三
思维辨析
随堂演练
5.已知两个非零向量a,b不共线,且ka+3b与2a+kb共线,求实数k的值.
解:因为ka+3b与2a+kb共线,
所以存在实数λ,使ka+3b=λ(2a+kb),
即ka+3b=2λa+λkb,即(k-2λ)a=(λk-3)b.
探究一
探究二
探究三
思维辨析
随堂演练
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
