高中数学人教A版2019必修第二册 6.2《向量的减法运算》教学设计一(表格式)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 6.2《向量的减法运算》教学设计一(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 347.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 21:48:38 | ||
图片预览

文档简介
《向量的加法运算》教学设计一
教学环节 教学内容 师生互动 设计意图
问题导入 在某地的一条大河中,水流速度为v1,摆渡船需要以v2的实际航速到达河对岸,那么摆渡船自身应以怎样的航行速度行驶呢 教师提出问题,引入课题. 学生思考. 从实际生活经历出发,激发学生的学习兴趣,同时体现向量的应用价值.
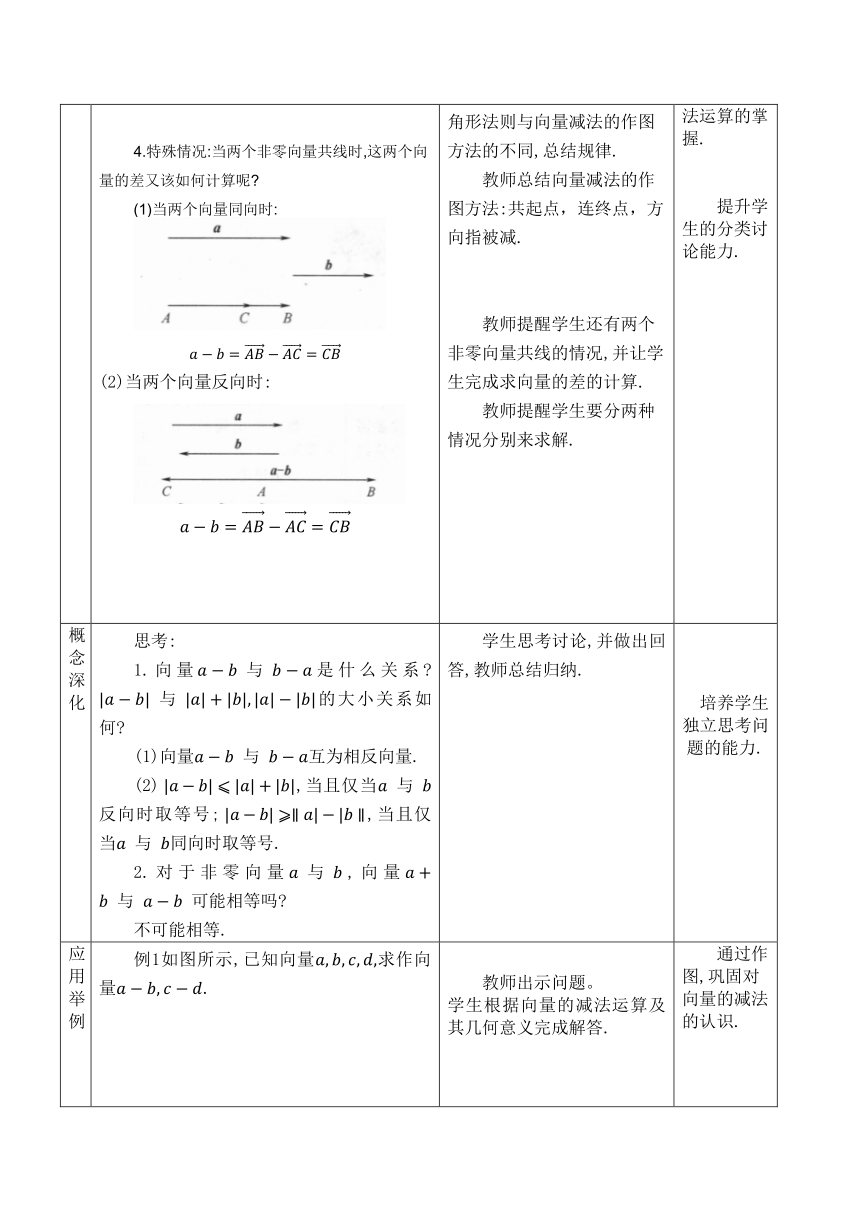
形成概念 1.相反向量. 与向量长度相等,方向相反的向量,叫做a的相反向量,记作 (如图所示). 互为相反向量, 我们规定:零向量的相反向量仍是零向量.任意向量与其相反向量的和是多少 2.向量的减法的概念. 向量加上的相反向量,叫做与的差,即求两个向量差的运算叫做向量的减法. 3.向量减法的几何意义. 已知向量a,b,在平面内任取一点O,作,.即可以表示为从向量b的终点指向向量的终点的向量,这是向量减法的几何意义. 4.特殊情况:当两个非零向量共线时,这两个向量的差又该如何计算呢 (1)当两个向量同向时: (2)当两个向量反向时: 学生独立完成相关概念的学习. 教师明确:任意向量与其相反向量的和是零向量.即如果,互为相反向量,那么=-,=-,+=0. 教师指导学生学习相关概念. 教师指出:向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量. 教师引导学生学习教材第11页图6.2-10的相关内容﹐得到的作图方法,进而得出向量减法的几何意义. 学生比较向量加法的三角形法则与向量减法的作图方法的不同,总结规律. 教师总结向量减法的作图方法:共起点,连终点,方向指被减. 教师提醒学生还有两个非零向量共线的情况,并让学生完成求向量的差的计算. 教师提醒学生要分两种情况分别来求解. 类比减法是加法的逆运算,加深对向量的减法的理解. 学习向量的减法的作图方法,有利于学生对向量的减法运算的掌握. 提升学生的分类讨论能力.
概念深化 思考: 1.向量是什么关系 的大小关系如何 (1)向量互为相反向量. (2),当且仅当反向时取等号;,当且仅当同向时取等号. 2.对于非零向量,向量可能相等吗 不可能相等. 学生思考讨论,并做出回答,教师总结归纳. 培养学生独立思考问题的能力.
应用举例 例1如图所示,已知向量求作向量. 解:如图所示,在平面上任取一点O,作,,, 例2如图所示,已知在口ABCD中,,试用向量分别表示向量. 解:由向量加法的平行四边形法则,得. 由向量的减法,得. 练习: 如图,在各小题中,已知向量,分别求作向量. 2.如下页图,四边形ABCD是平行四边形,BD与AC相交于点O,化简: 已知□,试用向量 分别表示以下向量: 教师出示问题。 学生根据向量的减法运算及其几何意义完成解答. 教师出示例题,让学生先小组讨论,再尝试写出解答过程. 集体订正,教师给出详细的解题步骤. 教师出示问题,结合学生解答情况纠错总结. 学生练习巩固.注意几种不同情况的向量减法的作图方法.在求向量减法的结果时,要注意是用减向量的终点指向被减向量的终点,教师要强调一定不能搞错. 通过作图,巩固对向量的减法的认识. 平行四边形是向量运算中经常遇到的图形,此题作为重点让学生熟练掌握. 练习中作图与化简两类题型都要练到,使学生对向量的减法的认识更加深刻.
归 纳 总 结 1.相反向量. 2.向量的减法的概念. 3.向量减法的几何意义. 学生自由发言,教师可针对学生薄弱或易错处进行强调和总结. 通过小结使学生加强对知识的记忆,养成总结的好习惯.
课后作业 教材第12~13页练习第1,2题. 学生课后独立完成. 巩固新知.
板书设计
6.2.2 向量的减法运算 一、问题导入 二,形成概念 1.相反向量 与向量长度相等,方向相反的向量,叫做的相反向量,记作. 规定:零向量的相反向量仍是零向量.任意向量与其相反向量的和是零向量. 2.向量的减法的概念 向量加上的相反向量,叫做 的差,即 求两个向量差的运算叫做向量的减法. 3.向量减法的几何意义 三﹑概念深化 ,当且仅当a 与b反向时取等号; ,当且仅当同向时取等号. 四、应用举例 例1 例2 五、归纳总结 六、课后作业
教学研讨
本节内容在设计上先由实际问题导入,然后给出相反向量的定义,再给出向量的减法运算.本节内容的概念深化环节,在确保学生对上述知识点掌握后思考几个问题,可以加深学生对向量的加减法、向量的模的了解.
教学环节 教学内容 师生互动 设计意图
问题导入 在某地的一条大河中,水流速度为v1,摆渡船需要以v2的实际航速到达河对岸,那么摆渡船自身应以怎样的航行速度行驶呢 教师提出问题,引入课题. 学生思考. 从实际生活经历出发,激发学生的学习兴趣,同时体现向量的应用价值.
形成概念 1.相反向量. 与向量长度相等,方向相反的向量,叫做a的相反向量,记作 (如图所示). 互为相反向量, 我们规定:零向量的相反向量仍是零向量.任意向量与其相反向量的和是多少 2.向量的减法的概念. 向量加上的相反向量,叫做与的差,即求两个向量差的运算叫做向量的减法. 3.向量减法的几何意义. 已知向量a,b,在平面内任取一点O,作,.即可以表示为从向量b的终点指向向量的终点的向量,这是向量减法的几何意义. 4.特殊情况:当两个非零向量共线时,这两个向量的差又该如何计算呢 (1)当两个向量同向时: (2)当两个向量反向时: 学生独立完成相关概念的学习. 教师明确:任意向量与其相反向量的和是零向量.即如果,互为相反向量,那么=-,=-,+=0. 教师指导学生学习相关概念. 教师指出:向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量. 教师引导学生学习教材第11页图6.2-10的相关内容﹐得到的作图方法,进而得出向量减法的几何意义. 学生比较向量加法的三角形法则与向量减法的作图方法的不同,总结规律. 教师总结向量减法的作图方法:共起点,连终点,方向指被减. 教师提醒学生还有两个非零向量共线的情况,并让学生完成求向量的差的计算. 教师提醒学生要分两种情况分别来求解. 类比减法是加法的逆运算,加深对向量的减法的理解. 学习向量的减法的作图方法,有利于学生对向量的减法运算的掌握. 提升学生的分类讨论能力.
概念深化 思考: 1.向量是什么关系 的大小关系如何 (1)向量互为相反向量. (2),当且仅当反向时取等号;,当且仅当同向时取等号. 2.对于非零向量,向量可能相等吗 不可能相等. 学生思考讨论,并做出回答,教师总结归纳. 培养学生独立思考问题的能力.
应用举例 例1如图所示,已知向量求作向量. 解:如图所示,在平面上任取一点O,作,,, 例2如图所示,已知在口ABCD中,,试用向量分别表示向量. 解:由向量加法的平行四边形法则,得. 由向量的减法,得. 练习: 如图,在各小题中,已知向量,分别求作向量. 2.如下页图,四边形ABCD是平行四边形,BD与AC相交于点O,化简: 已知□,试用向量 分别表示以下向量: 教师出示问题。 学生根据向量的减法运算及其几何意义完成解答. 教师出示例题,让学生先小组讨论,再尝试写出解答过程. 集体订正,教师给出详细的解题步骤. 教师出示问题,结合学生解答情况纠错总结. 学生练习巩固.注意几种不同情况的向量减法的作图方法.在求向量减法的结果时,要注意是用减向量的终点指向被减向量的终点,教师要强调一定不能搞错. 通过作图,巩固对向量的减法的认识. 平行四边形是向量运算中经常遇到的图形,此题作为重点让学生熟练掌握. 练习中作图与化简两类题型都要练到,使学生对向量的减法的认识更加深刻.
归 纳 总 结 1.相反向量. 2.向量的减法的概念. 3.向量减法的几何意义. 学生自由发言,教师可针对学生薄弱或易错处进行强调和总结. 通过小结使学生加强对知识的记忆,养成总结的好习惯.
课后作业 教材第12~13页练习第1,2题. 学生课后独立完成. 巩固新知.
板书设计
6.2.2 向量的减法运算 一、问题导入 二,形成概念 1.相反向量 与向量长度相等,方向相反的向量,叫做的相反向量,记作. 规定:零向量的相反向量仍是零向量.任意向量与其相反向量的和是零向量. 2.向量的减法的概念 向量加上的相反向量,叫做 的差,即 求两个向量差的运算叫做向量的减法. 3.向量减法的几何意义 三﹑概念深化 ,当且仅当a 与b反向时取等号; ,当且仅当同向时取等号. 四、应用举例 例1 例2 五、归纳总结 六、课后作业
教学研讨
本节内容在设计上先由实际问题导入,然后给出相反向量的定义,再给出向量的减法运算.本节内容的概念深化环节,在确保学生对上述知识点掌握后思考几个问题,可以加深学生对向量的加减法、向量的模的了解.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
