高中数学人教A版2019必修第二册 6.2.1 向量的加法运算 导学案(含答案)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 6.2.1 向量的加法运算 导学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 367.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-22 21:56:12 | ||
图片预览


文档简介
6.2.1 向量的加法运算
1、掌握向量的加法运算,并理解其几何意义;
2、会用向量加法的三角形法则和平行四边形法则作两个向量的和向量,培养数形结合解决问题的能力;
3、通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,并会用它们进行向量计算,渗透类比的数学方法.
1.数学抽象:向量加法概念;
2.逻辑推理:利用向量加法证明几何问题;
3.直观想象:向量加法运算;
4.数学建模:从实际问题抽象出数学模型,数形结合,运用向量加法解决实际问题.
重点:会用向量加法的三角形法则和平行四边形法则作两个向量的和向量;
难点:理解向量加法的定义.
预习导入
阅读课本7-10页,填写。
1、向量的加法:_______________________________________.
2、三角形法则和平行四边形法则
(1)三角形法则(“首尾相接,首尾连”)
如图,已知向量a、b.在平面内任取一点,作=a,=b,则向量叫做a与b的和,记作a+b,即 a+b, 规定: a + 0= 0 + a
(2)平行四边形法则
如图所示:=+(三角形法则) ,又因为=,
所以=+(平行四边形法则),
注意:在使用三角形法则时,应注意“首尾连接”,这个方法可推广到多个向量相加的情形;在使用平行四边形法则时,应注意范围的限制及和向量与两向量起点相同.
3.向量a+b与非零向量a,b的模及方向的关系
(1)当a与b不共线时,a+b的方向与a,b都不相同,且|a+b|____|a|+|b|.
(2)当a与b同向时,a+b,a,b的方向相同,且|a+b|=____________.
(3)当a与b反向时,若|a|≥|b|,则a+b与a的方向相同,且|a+b|=__________.
若|a|<|b|,则a+b与b的方向相同,且|a+b|=__________.
4.向量加法的运算律
(1)交换律:a+b=___________;
(2)结合律:a+b+c=_____________=_____________.
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)两个向量相加结果可能是一个数量.( )
(2)两个向量相加实际上就是两个向量的模相加.( )
(3)任意两个向量的和向量不可能与这两个向量共线.( )
2.对任意四边形ABCD,下列式子中不等于的是( )
A.+ B.++
C.++ D.++
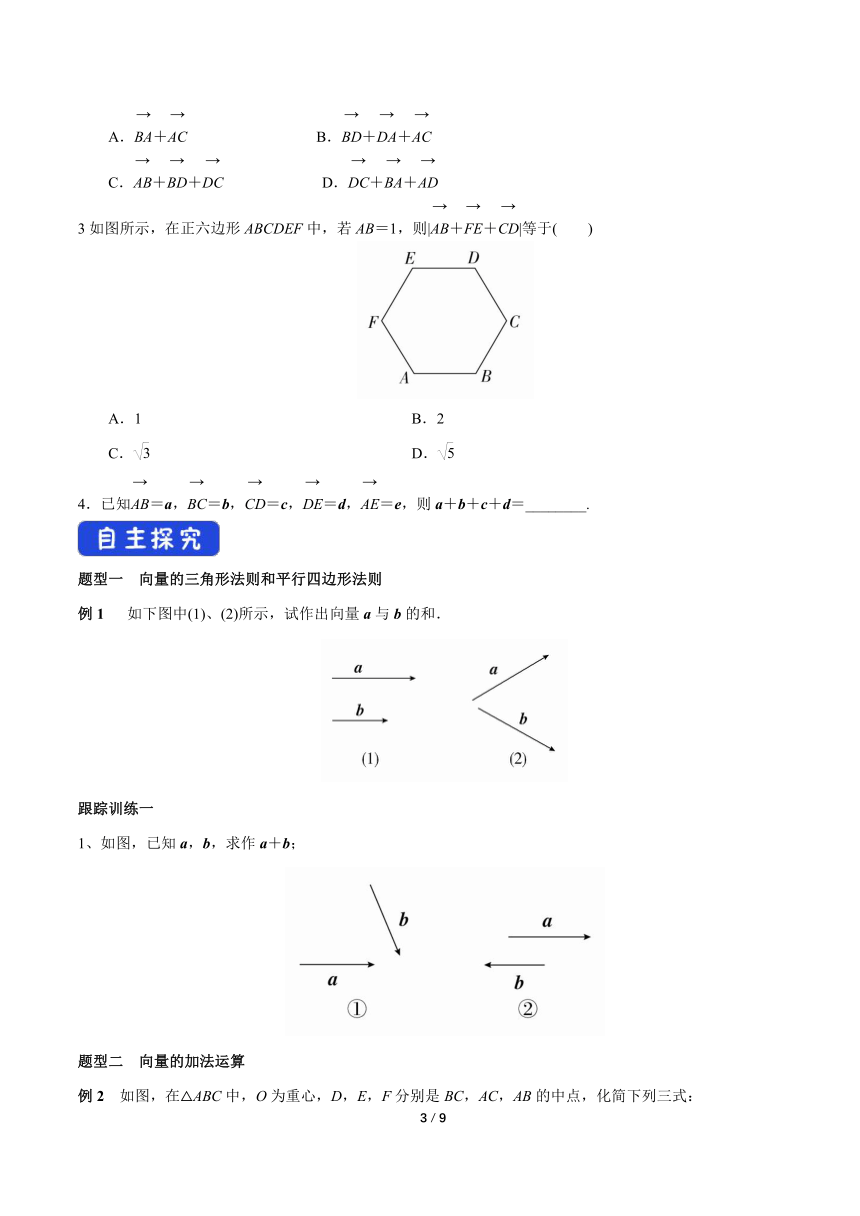
3如图所示,在正六边形ABCDEF中,若AB=1,则|++|等于( )
A.1 B.2
C. D.
4.已知=a,=b,=c,=d,=e,则a+b+c+d=________.
题型一 向量的三角形法则和平行四边形法则
例1 如下图中(1)、(2)所示,试作出向量a与b的和.
跟踪训练一
1、如图,已知a,b,求作a+b;
题型二 向量的加法运算
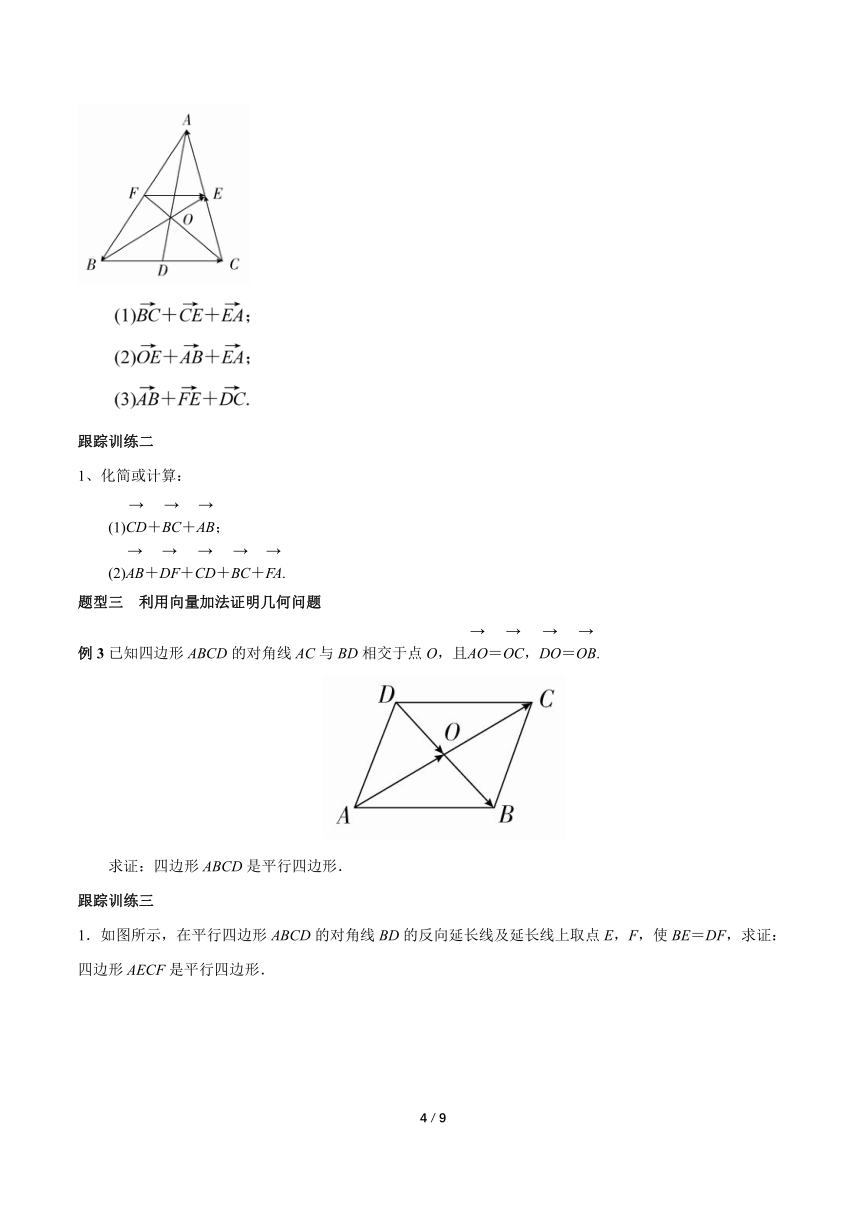
例2 如图,在△ABC中,O为重心,D,E,F分别是BC,AC,AB的中点,化简下列三式:
跟踪训练二
1、化简或计算:
(1)++;
(2)++++.
题型三 利用向量加法证明几何问题
例3已知四边形ABCD的对角线AC与BD相交于点O,且=,=.
求证:四边形ABCD是平行四边形.
跟踪训练三
1.如图所示,在平行四边形ABCD的对角线BD的反向延长线及延长线上取点E,F,使BE=DF,求证:四边形AECF是平行四边形.
题型四 向量加法的实际应用
例4 在水流速度为向东10 km/h的河中,如果要使船实际航行的速度的大小为10 km/h,方向垂直于对岸渡河,求船行驶速度的大小与方向.
跟踪训练四
1、在某地抗震救灾中,一救护车从A地按北偏东35°的方向行驶800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向行驶800 km送往C地医院,求这辆救护车行驶的路程及两次位移的和.
1.在平行四边形ABCD中,下列式子:
①=+;②=+;③+=;④+=;⑤=++;⑥=+.
其中不正确的个数是( )
A.1 B.2 C.4 D.6
2.设a=(+)+(+),b是任一非零向量,则在下列结论中,正确的是( )
①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|;
⑤|a+b|=|a|+|b|.
A.①② B.①③
C.①③⑤ D.②④⑤
3.已知△ABC的三个顶点A,B,C及平面内一点P满足+=,则下列结论中正确的是( )
A.P在△ABC的内部
B.P在△ABC的边AB上
C.P在AB边所在的直线上
D.P在△ABC的外部
4.根据图示填空.
(1)+=________;
(2)++=________;
(3)++2=________.
5.若P为△ABC的外心,且+=,则∠ACB=________.
6.已知矩形ABCD中,宽为2,长为2,=a,=b,=c,试作出向量a+b+c,并求出其模的大小.
答案
小试牛刀
1. (1)×(2) ×(3)×
2.C.
3.B.
4. e
自主探究
例1 【答案】见解析
【解析】如下图中(1)、(2)所示,
首先作=a,然后作=b,则=a+b.
跟踪训练一
1、【答案】见解析.
【解析】如图所示.
.
例2 【答案】 (1) . (2) . (3) ..
【解析】 (1)++=+=.
(2)++=(+)+=+=.
(3)++=++=+=.
跟踪训练二
1、【答案】(1). (2) 0.
【解析】(1)++=(+)+=+=.
(2)++++=(+)+(+)+=++=+=0.
例3【答案】见解析.
【解析】证明 =+,=+,
又∵=,=,∴=,
∴AB=DC且AB∥DC,
∴四边形ABCD为平行四边形.
跟踪训练三
1.【答案】见解析.
【解析】证明 ∵=+,=+,
又=,=,
∴=,即AE与FC平行且相等.
∴四边形AECF是平行四边形.
例4 【答案】 船行驶速度为20 km/h,方向与水流方向的夹角为120°.
【解析】 如图所示,表示水速,表示船实际航行的速度,表示船速,
由=+易知||=||=10,又∠OBC=90°,所以||=20,
所以∠BOC=30°,所以∠AOC=120°,即船行驶速度为20 km/h,
方向与水流方向的夹角为120°.
跟踪训练四
1、【答案】救护车行驶的路程是1600 km,两次行驶的位移和的大小为800 km,方向为北偏东80°.
【解析】如图所示,设,分别表示救护车从A地按北偏东35°方向行驶800 km,从B地按南偏东55°的方向行驶800 km.
则救护车行驶的路程指的是||+||;
两次行驶的位移的和指的是+=.
依题意,有||+||=800+800=1600(km).
又α=35°,β=55°,∠ABC=35°+55°=90°.所以||===800(km).
其中∠BAC=45°,所以方向为北偏东35°+45°=80°.
从而救护车行驶的路程是1600 km,两次行驶的位移和的大小为800 km,方向为北偏东80°.
当堂检测
1-3.ACD4. (1) (2) (3)+5. 120°
6. 【答案】8.
【解析】作=,如图,则a+b+c=,
a+b+c=++=2=2c,∴|a+b+c|=|2|=2=8.
1 / 9
1、掌握向量的加法运算,并理解其几何意义;
2、会用向量加法的三角形法则和平行四边形法则作两个向量的和向量,培养数形结合解决问题的能力;
3、通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,并会用它们进行向量计算,渗透类比的数学方法.
1.数学抽象:向量加法概念;
2.逻辑推理:利用向量加法证明几何问题;
3.直观想象:向量加法运算;
4.数学建模:从实际问题抽象出数学模型,数形结合,运用向量加法解决实际问题.
重点:会用向量加法的三角形法则和平行四边形法则作两个向量的和向量;
难点:理解向量加法的定义.
预习导入
阅读课本7-10页,填写。
1、向量的加法:_______________________________________.
2、三角形法则和平行四边形法则
(1)三角形法则(“首尾相接,首尾连”)
如图,已知向量a、b.在平面内任取一点,作=a,=b,则向量叫做a与b的和,记作a+b,即 a+b, 规定: a + 0= 0 + a
(2)平行四边形法则
如图所示:=+(三角形法则) ,又因为=,
所以=+(平行四边形法则),
注意:在使用三角形法则时,应注意“首尾连接”,这个方法可推广到多个向量相加的情形;在使用平行四边形法则时,应注意范围的限制及和向量与两向量起点相同.
3.向量a+b与非零向量a,b的模及方向的关系
(1)当a与b不共线时,a+b的方向与a,b都不相同,且|a+b|____|a|+|b|.
(2)当a与b同向时,a+b,a,b的方向相同,且|a+b|=____________.
(3)当a与b反向时,若|a|≥|b|,则a+b与a的方向相同,且|a+b|=__________.
若|a|<|b|,则a+b与b的方向相同,且|a+b|=__________.
4.向量加法的运算律
(1)交换律:a+b=___________;
(2)结合律:a+b+c=_____________=_____________.
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)两个向量相加结果可能是一个数量.( )
(2)两个向量相加实际上就是两个向量的模相加.( )
(3)任意两个向量的和向量不可能与这两个向量共线.( )
2.对任意四边形ABCD,下列式子中不等于的是( )
A.+ B.++
C.++ D.++
3如图所示,在正六边形ABCDEF中,若AB=1,则|++|等于( )
A.1 B.2
C. D.
4.已知=a,=b,=c,=d,=e,则a+b+c+d=________.
题型一 向量的三角形法则和平行四边形法则
例1 如下图中(1)、(2)所示,试作出向量a与b的和.
跟踪训练一
1、如图,已知a,b,求作a+b;
题型二 向量的加法运算
例2 如图,在△ABC中,O为重心,D,E,F分别是BC,AC,AB的中点,化简下列三式:
跟踪训练二
1、化简或计算:
(1)++;
(2)++++.
题型三 利用向量加法证明几何问题
例3已知四边形ABCD的对角线AC与BD相交于点O,且=,=.
求证:四边形ABCD是平行四边形.
跟踪训练三
1.如图所示,在平行四边形ABCD的对角线BD的反向延长线及延长线上取点E,F,使BE=DF,求证:四边形AECF是平行四边形.
题型四 向量加法的实际应用
例4 在水流速度为向东10 km/h的河中,如果要使船实际航行的速度的大小为10 km/h,方向垂直于对岸渡河,求船行驶速度的大小与方向.
跟踪训练四
1、在某地抗震救灾中,一救护车从A地按北偏东35°的方向行驶800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向行驶800 km送往C地医院,求这辆救护车行驶的路程及两次位移的和.
1.在平行四边形ABCD中,下列式子:
①=+;②=+;③+=;④+=;⑤=++;⑥=+.
其中不正确的个数是( )
A.1 B.2 C.4 D.6
2.设a=(+)+(+),b是任一非零向量,则在下列结论中,正确的是( )
①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|;
⑤|a+b|=|a|+|b|.
A.①② B.①③
C.①③⑤ D.②④⑤
3.已知△ABC的三个顶点A,B,C及平面内一点P满足+=,则下列结论中正确的是( )
A.P在△ABC的内部
B.P在△ABC的边AB上
C.P在AB边所在的直线上
D.P在△ABC的外部
4.根据图示填空.
(1)+=________;
(2)++=________;
(3)++2=________.
5.若P为△ABC的外心,且+=,则∠ACB=________.
6.已知矩形ABCD中,宽为2,长为2,=a,=b,=c,试作出向量a+b+c,并求出其模的大小.
答案
小试牛刀
1. (1)×(2) ×(3)×
2.C.
3.B.
4. e
自主探究
例1 【答案】见解析
【解析】如下图中(1)、(2)所示,
首先作=a,然后作=b,则=a+b.
跟踪训练一
1、【答案】见解析.
【解析】如图所示.
.
例2 【答案】 (1) . (2) . (3) ..
【解析】 (1)++=+=.
(2)++=(+)+=+=.
(3)++=++=+=.
跟踪训练二
1、【答案】(1). (2) 0.
【解析】(1)++=(+)+=+=.
(2)++++=(+)+(+)+=++=+=0.
例3【答案】见解析.
【解析】证明 =+,=+,
又∵=,=,∴=,
∴AB=DC且AB∥DC,
∴四边形ABCD为平行四边形.
跟踪训练三
1.【答案】见解析.
【解析】证明 ∵=+,=+,
又=,=,
∴=,即AE与FC平行且相等.
∴四边形AECF是平行四边形.
例4 【答案】 船行驶速度为20 km/h,方向与水流方向的夹角为120°.
【解析】 如图所示,表示水速,表示船实际航行的速度,表示船速,
由=+易知||=||=10,又∠OBC=90°,所以||=20,
所以∠BOC=30°,所以∠AOC=120°,即船行驶速度为20 km/h,
方向与水流方向的夹角为120°.
跟踪训练四
1、【答案】救护车行驶的路程是1600 km,两次行驶的位移和的大小为800 km,方向为北偏东80°.
【解析】如图所示,设,分别表示救护车从A地按北偏东35°方向行驶800 km,从B地按南偏东55°的方向行驶800 km.
则救护车行驶的路程指的是||+||;
两次行驶的位移的和指的是+=.
依题意,有||+||=800+800=1600(km).
又α=35°,β=55°,∠ABC=35°+55°=90°.所以||===800(km).
其中∠BAC=45°,所以方向为北偏东35°+45°=80°.
从而救护车行驶的路程是1600 km,两次行驶的位移和的大小为800 km,方向为北偏东80°.
当堂检测
1-3.ACD4. (1) (2) (3)+5. 120°
6. 【答案】8.
【解析】作=,如图,则a+b+c=,
a+b+c=++=2=2c,∴|a+b+c|=|2|=2=8.
1 / 9
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
