4.4.1 对数函数的概念 课件(共25张PPT)
文档属性
| 名称 | 4.4.1 对数函数的概念 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
数学人教版必修第一册第四章指数函数与对数函数4.4.1 对数函数的概念授课人:魏永祥问题1
【问题探究】
那么1个这样的细胞分裂3次得到细胞个数y是多少呢?如何计算
某种细胞分裂时,1个分裂成2个,2个分裂成4 个,…,依次类推
若1个这样的细胞分裂4次得到细胞个数y又是多少呢?
若果1个这样的细胞分裂x次得到细胞个数y又是多少呢?
问题2
若果1个这样的细胞分裂得到的细胞个数为32,
请问细胞分裂的次数x是多少呢?如何计算
若果1个这样的细胞分裂得到的细胞个数为y,
请问细胞分裂的次数x是多少呢?如何表示
问题3
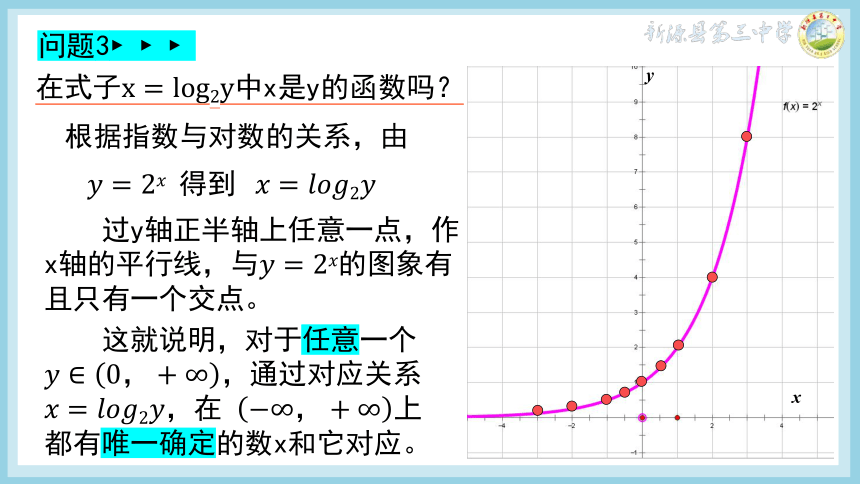
在式子x是y的函数吗?
x
y
根据指数与对数的关系,由
过y轴正半轴上任意一点,作x轴的平行线,与的图象有且只有一个交点。
这就说明,对于任意一个,通过对应关系
在 上
都有唯一确定的数x和它对应。
所以也是的函数.也就是说,
函数
刻画了x随y的增长而变化的规律.
同样地,根据指数与对数的关系,
由可以得到
通常,我们用表示自变量,表示函数.
为此,将
中的字母和对调,写成
也是的函数.
【新知生成】
对数函数的概念
函数叫做对数函数,其中是自变量,函数的定义域是(0,+∞).
特别地,
我们称以10为底的对数函数y=为常用对数函数;
称以无理数e为底的对数函数y=lnx为自然对数函数.
【课堂小练】
1.判断题
(1)函数y=logx是对数函数. ( )
(2)函数y=2log3x是对数函数. ( )
(3)函数y=log2(3x-2)是对数函数.( )
(4)函数y=log(x-1)x是对数函数. ( )
判断一个函数是不是对数函数,关键是分析所给函数是否具有y=logax(a>0,且a≠1)这种形式.
(1)对数符号前面的系数是1;
(2)对数的底数是大于零且不等于1的常数;
(3)对数的真数仅有自变量x.
【课堂小练】
下列函数是对数函数的有( )
①y=x;②y=1+log3x;
③y=lnx; ④y=(log3x)2.
2.选择题
A.1个 B.2个 C.3个 D.4个
【课堂小练】
3.若函数f(x)=log(a+1)x+(a2-2a-8)是对数函数,
则a=________.
解:由对数函数的定义可知
解得 a=4.
【例题讲解】
例1 求下列函数的定义域:
(1)
(2)
对数式有意义:底数大于0且不等于1,真数大于0.
【例题讲解】
例1 求下列函数的定义域:
(1)
(2)
解:(1)因为>0,即≠0,所以函数
的定义域是{|≠0}.
(2)因为>0,即<,所以函数
的定义域是
{|<}.
对数式有意义:底数大于0且不等于1,真数大于0.
(1) (2)
(3)
【跟踪训练1】求下列函数的定义域:
例 2 点A(8,-3)和B(n,2)在同一个对数函数图象上,则n=_____
【例题讲解】
例 2 点A(8,-3)和B(n,2)在同一个对数函数图象上,则n=_____
【例题讲解】
解:设对数函数为f(x)=logax(a>0,且a≠1).
由题意可得f(8)=-3,即loga8=-3,
解得a=所以f(x)=
又B(n,2)在这个对数函数图象上故f(n)==2
解得a=
某地为了抑制一种有害昆虫的繁殖,引入了一种以该昆虫为食物的特殊动物,已知该动物的繁殖数量y(只)与引入时间x(年)的关系为y=alog2(x+1),若该动物在引入一年后的数量为100只,则第7年它们发展到( )A.300只 B.400只 C.600只 D.700只
【跟踪训练2】
某地为了抑制一种有害昆虫的繁殖,引入了一种以该昆虫为食物的特殊动物,已知该动物的繁殖数量y(只)与引入时间x(年)的关系为y=alog2(x+1),若该动物在引入一年后的数量为100只,则第7年它们发展到( )A.300只 B.400只 C.600只 D.700只
【跟踪训练2】
解: 将x=1,y=100代入y=alog2(x+1)得,
100=alog2(1+1),解得a=100,
所以x=7时,y=100log2(7+1)=300.
例 3 假设某地初始物价为1,每年以5%的增长率递增,
经过y年后的物价为x.(1)该地的物价经过几年后会翻一番?(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
【例题讲解】
例 3 假设某地初始物价为1,每年以5%的增长率递增,
经过y年后的物价为x.
(1)该地的物价经过几年后会翻一番?
【例题讲解】
解:(1)由题意可知,经过y年后物价x为
x=(1+5%),即x=1.05( ∈[0,+∞))
由对数与指数间的关系,可得
,∈[1,+∞)
由计算工具可得,当=2时,≈14.
所以,该地区的物价大约经过14年后会翻一番.
例 3 假设某地初始物价为1,每年以5%的增长率递增,
经过y年后的物价为x.(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
【例题讲解】
解:(2)根据函数,∈[1,+∞),
利用计算工具,可得下表:
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约每增加1倍所需要的时间在逐渐缩小.
【教学小结】
爱学习的孩子才是好孩子
函数
叫做对数函数,其中是自变量,函数的定义域是(0,+∞).
(1)对数符号前面的系数是1
(2)对数的底数是大于零
且不等于1的常数;
(3)对数的真数仅有自变量x
1.下列函数表达式中,是对数函数的有( )①y=logx2;②y=logax(a∈R);③y=log8x;④y=ln x;⑤y=logx(x+2);⑥y=2log4x;⑦y=log2(x+1). A.1个 C.3个 D.4个
【课后练习】
2.求下列函数的定义域:
(1)y=log2(16-4x);(2)y=log(x-1)(3-x).
B.2个
1.下列函数表达式中,是对数函数的有( )①y=logx2;②y=logax(a∈R);③y=log8x;④y=ln x;⑤y=logx(x+2);⑥y=2log4x;⑦y=log2(x+1). A.1个 C.3个 D.4个
【课后练习】
2.求下列函数的定义域:
(1)y=log2(16-4x);(2)y=log(x-1)(3-x).
{x|x<2}
{x|x>1,且x≠2}
B.2个
3.我们知道,燕子每年秋天都要从北方飞到南方过冬.研究燕子的科学家发现,两岁燕子的飞行速度可以表示为函数=5log2(单位:m/s),其中表示燕子的耗氧量.(1)计算一只两岁燕子静止时的耗氧量是多少个单位;(2)当一只两岁燕子的耗氧量为80个单位时,它的飞行速度是多少?
【课后练习】
解: (1)当燕子静止时,=0,故有 0=5log2,
所以log2=0,=10,即一只两岁燕子静
止时的耗 氧量是10个单位.
【课后练习】
(2)一只两岁燕子的耗氧量为80个单位时,
它的飞行速度=5log2=5×3=15(m/s).
谢谢大家
数学人教版必修第一册第四章指数函数与对数函数4.4.1 对数函数的概念授课人:魏永祥问题1
【问题探究】
那么1个这样的细胞分裂3次得到细胞个数y是多少呢?如何计算
某种细胞分裂时,1个分裂成2个,2个分裂成4 个,…,依次类推
若1个这样的细胞分裂4次得到细胞个数y又是多少呢?
若果1个这样的细胞分裂x次得到细胞个数y又是多少呢?
问题2
若果1个这样的细胞分裂得到的细胞个数为32,
请问细胞分裂的次数x是多少呢?如何计算
若果1个这样的细胞分裂得到的细胞个数为y,
请问细胞分裂的次数x是多少呢?如何表示
问题3
在式子x是y的函数吗?
x
y
根据指数与对数的关系,由
过y轴正半轴上任意一点,作x轴的平行线,与的图象有且只有一个交点。
这就说明,对于任意一个,通过对应关系
在 上
都有唯一确定的数x和它对应。
所以也是的函数.也就是说,
函数
刻画了x随y的增长而变化的规律.
同样地,根据指数与对数的关系,
由可以得到
通常,我们用表示自变量,表示函数.
为此,将
中的字母和对调,写成
也是的函数.
【新知生成】
对数函数的概念
函数叫做对数函数,其中是自变量,函数的定义域是(0,+∞).
特别地,
我们称以10为底的对数函数y=为常用对数函数;
称以无理数e为底的对数函数y=lnx为自然对数函数.
【课堂小练】
1.判断题
(1)函数y=logx是对数函数. ( )
(2)函数y=2log3x是对数函数. ( )
(3)函数y=log2(3x-2)是对数函数.( )
(4)函数y=log(x-1)x是对数函数. ( )
判断一个函数是不是对数函数,关键是分析所给函数是否具有y=logax(a>0,且a≠1)这种形式.
(1)对数符号前面的系数是1;
(2)对数的底数是大于零且不等于1的常数;
(3)对数的真数仅有自变量x.
【课堂小练】
下列函数是对数函数的有( )
①y=x;②y=1+log3x;
③y=lnx; ④y=(log3x)2.
2.选择题
A.1个 B.2个 C.3个 D.4个
【课堂小练】
3.若函数f(x)=log(a+1)x+(a2-2a-8)是对数函数,
则a=________.
解:由对数函数的定义可知
解得 a=4.
【例题讲解】
例1 求下列函数的定义域:
(1)
(2)
对数式有意义:底数大于0且不等于1,真数大于0.
【例题讲解】
例1 求下列函数的定义域:
(1)
(2)
解:(1)因为>0,即≠0,所以函数
的定义域是{|≠0}.
(2)因为>0,即<,所以函数
的定义域是
{|<}.
对数式有意义:底数大于0且不等于1,真数大于0.
(1) (2)
(3)
【跟踪训练1】求下列函数的定义域:
例 2 点A(8,-3)和B(n,2)在同一个对数函数图象上,则n=_____
【例题讲解】
例 2 点A(8,-3)和B(n,2)在同一个对数函数图象上,则n=_____
【例题讲解】
解:设对数函数为f(x)=logax(a>0,且a≠1).
由题意可得f(8)=-3,即loga8=-3,
解得a=所以f(x)=
又B(n,2)在这个对数函数图象上故f(n)==2
解得a=
某地为了抑制一种有害昆虫的繁殖,引入了一种以该昆虫为食物的特殊动物,已知该动物的繁殖数量y(只)与引入时间x(年)的关系为y=alog2(x+1),若该动物在引入一年后的数量为100只,则第7年它们发展到( )A.300只 B.400只 C.600只 D.700只
【跟踪训练2】
某地为了抑制一种有害昆虫的繁殖,引入了一种以该昆虫为食物的特殊动物,已知该动物的繁殖数量y(只)与引入时间x(年)的关系为y=alog2(x+1),若该动物在引入一年后的数量为100只,则第7年它们发展到( )A.300只 B.400只 C.600只 D.700只
【跟踪训练2】
解: 将x=1,y=100代入y=alog2(x+1)得,
100=alog2(1+1),解得a=100,
所以x=7时,y=100log2(7+1)=300.
例 3 假设某地初始物价为1,每年以5%的增长率递增,
经过y年后的物价为x.(1)该地的物价经过几年后会翻一番?(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
【例题讲解】
例 3 假设某地初始物价为1,每年以5%的增长率递增,
经过y年后的物价为x.
(1)该地的物价经过几年后会翻一番?
【例题讲解】
解:(1)由题意可知,经过y年后物价x为
x=(1+5%),即x=1.05( ∈[0,+∞))
由对数与指数间的关系,可得
,∈[1,+∞)
由计算工具可得,当=2时,≈14.
所以,该地区的物价大约经过14年后会翻一番.
例 3 假设某地初始物价为1,每年以5%的增长率递增,
经过y年后的物价为x.(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
【例题讲解】
解:(2)根据函数,∈[1,+∞),
利用计算工具,可得下表:
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约每增加1倍所需要的时间在逐渐缩小.
【教学小结】
爱学习的孩子才是好孩子
函数
叫做对数函数,其中是自变量,函数的定义域是(0,+∞).
(1)对数符号前面的系数是1
(2)对数的底数是大于零
且不等于1的常数;
(3)对数的真数仅有自变量x
1.下列函数表达式中,是对数函数的有( )①y=logx2;②y=logax(a∈R);③y=log8x;④y=ln x;⑤y=logx(x+2);⑥y=2log4x;⑦y=log2(x+1). A.1个 C.3个 D.4个
【课后练习】
2.求下列函数的定义域:
(1)y=log2(16-4x);(2)y=log(x-1)(3-x).
B.2个
1.下列函数表达式中,是对数函数的有( )①y=logx2;②y=logax(a∈R);③y=log8x;④y=ln x;⑤y=logx(x+2);⑥y=2log4x;⑦y=log2(x+1). A.1个 C.3个 D.4个
【课后练习】
2.求下列函数的定义域:
(1)y=log2(16-4x);(2)y=log(x-1)(3-x).
{x|x<2}
{x|x>1,且x≠2}
B.2个
3.我们知道,燕子每年秋天都要从北方飞到南方过冬.研究燕子的科学家发现,两岁燕子的飞行速度可以表示为函数=5log2(单位:m/s),其中表示燕子的耗氧量.(1)计算一只两岁燕子静止时的耗氧量是多少个单位;(2)当一只两岁燕子的耗氧量为80个单位时,它的飞行速度是多少?
【课后练习】
解: (1)当燕子静止时,=0,故有 0=5log2,
所以log2=0,=10,即一只两岁燕子静
止时的耗 氧量是10个单位.
【课后练习】
(2)一只两岁燕子的耗氧量为80个单位时,
它的飞行速度=5log2=5×3=15(m/s).
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
