9.3三角形的高.中线与角平分线

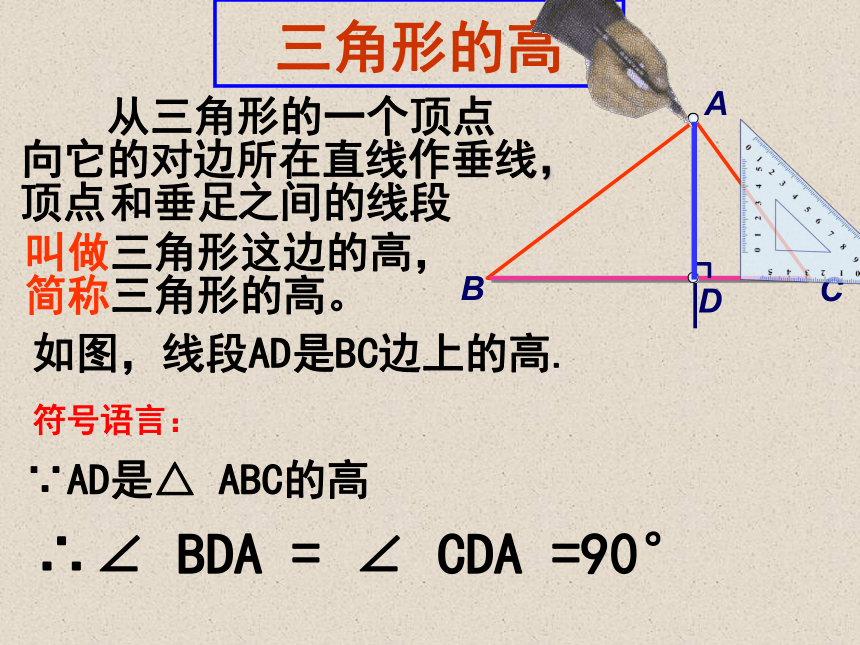
课件37张PPT。三角形的高.中线与角平分线你还记得 “过一点画已知直线的垂线” 吗?三角形的高A 从三角形的一个顶点BC向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形这边的高，简称三角形的高。如图，线段AD是BC边上的高.符号语言：∵AD是△ ABC的高
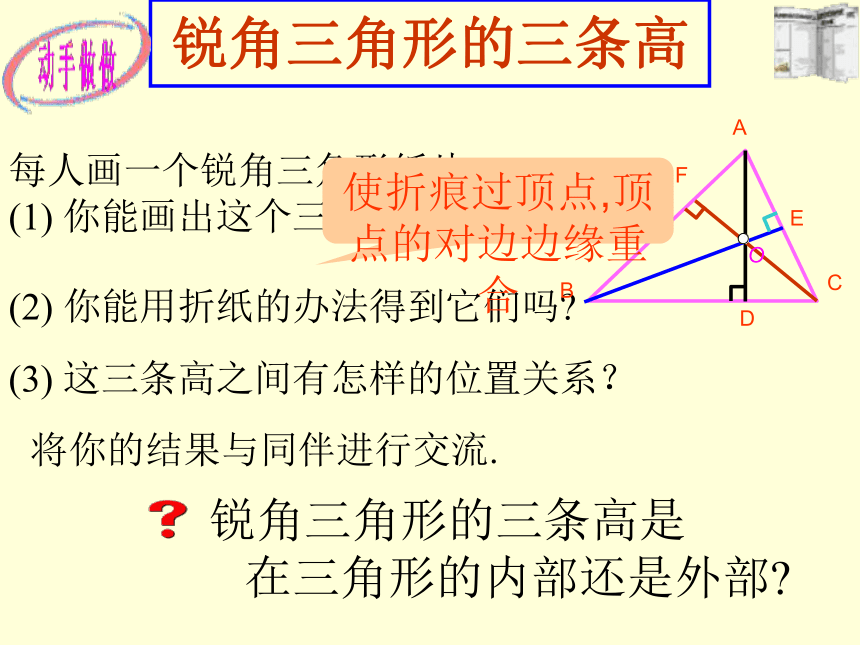
∴∠ BDA = ∠ CDA =90°锐角三角形的三条高每人画一个锐角三角形纸片。
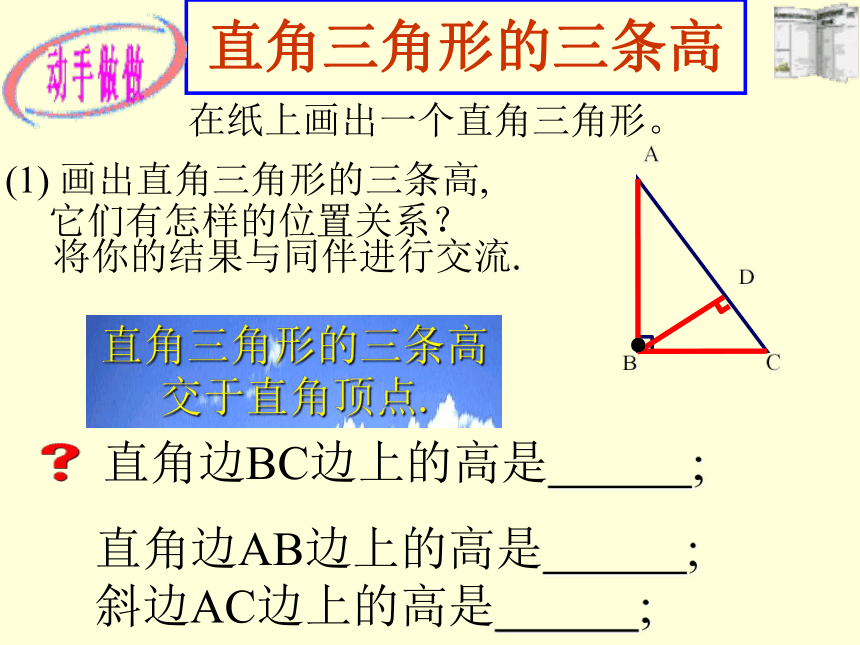
(1) 你能画出这个三角形的三条高吗?(3) 这三条高之间有怎样的位置关系？将你的结果与同伴进行交流.(2) 你能用折纸的办法得到它们吗?ABCDEF使折痕过顶点,顶点的对边边缘重合直角三角形的三条高在纸上画出一个直角三角形。将你的结果与同伴进行交流.ABC(1) 画出直角三角形的三条高,直角边AB边上的高是 ;它们有怎样的位置关系？直角三角形的三条高交于直角顶点.D斜边AC边上的高是 ;●钝角三角形的三条高DEF(1) 钝角三角形的
三条高交于一点吗？钝角三角形的三条高不相交于一点它们所在的直线交于一点吗？将你的结果与同伴进行交流.钝角三角形的三条高所在直线交于一点O311相交相交不相交相交相交相交三角形
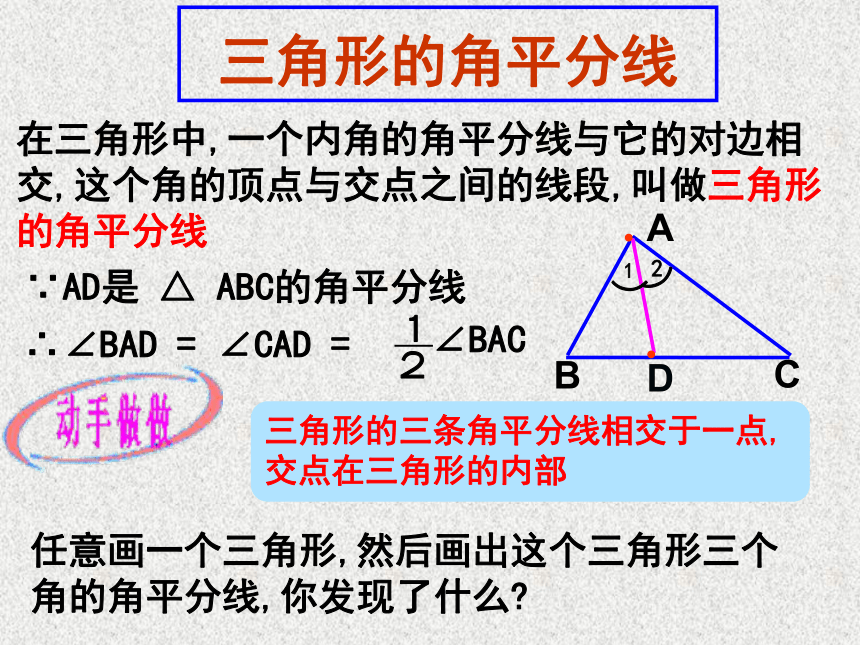
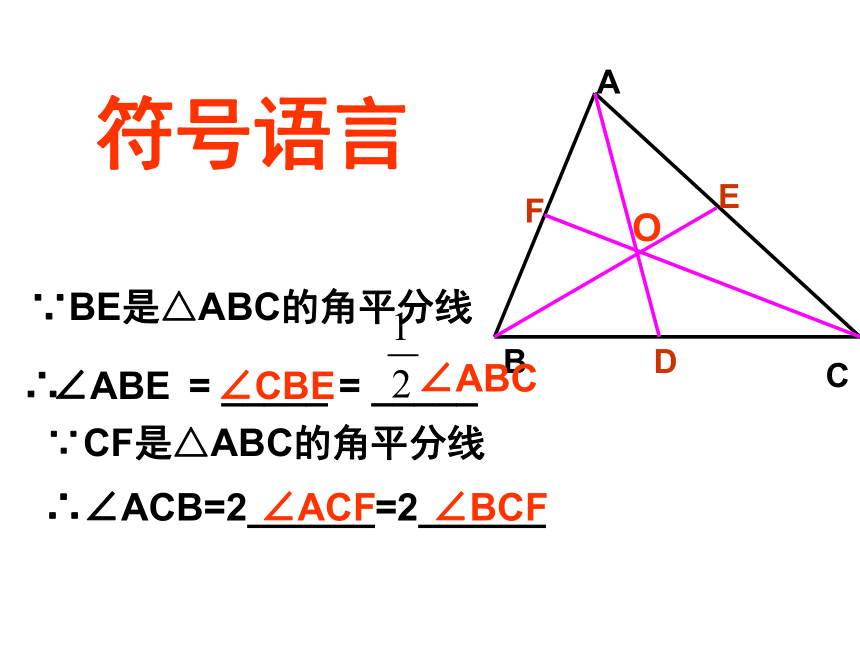
内部直角顶点三角形外部三角形的三条高所在直线交于一点三角形的角平分线ABCD∵AD是 △ ABC的角平分线任意画一个三角形,然后画出这个三角形三个角的角平分线,你发现了什么?●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线●三角形的三条角平分线相交于一点,交点在三角形的内部ACBFEDO∵BE是△ABC的角平分线∴ = _____ = _____∴∠ACB=2______=2______∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF符号语言 三角形的角平分线与角的平分线有什么区别？思考三角形的角平分线是一条线段 , 角的平分线是一条射线三角形的中线在三角形中,连接一个顶点和它对边中点的线段叫做这个三角形的中线D∵AD是△ABC的中线
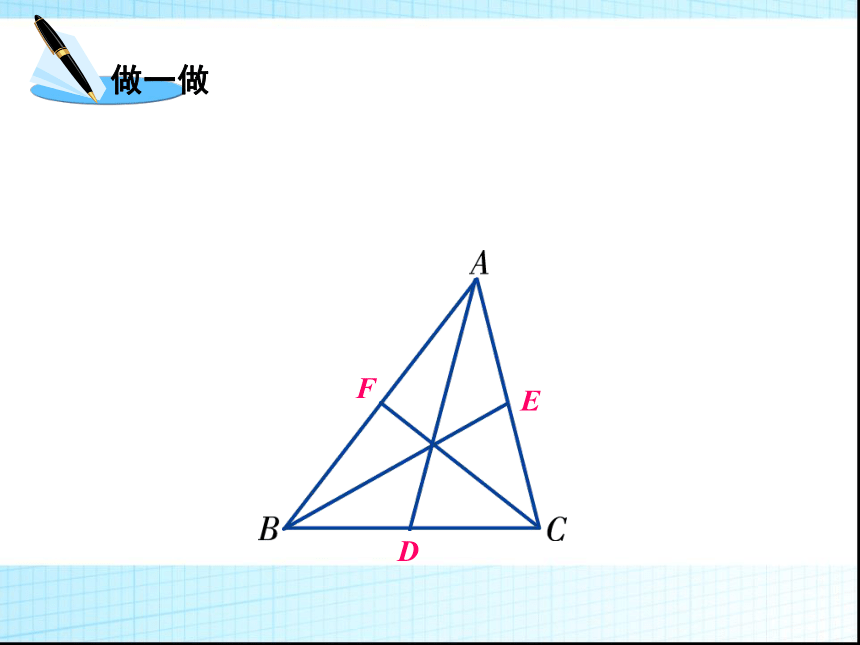
任意画一个三角形,然后画出这个三角形三条边的中线,你发现了什么?●●三角形的三条中线相交于一点,交点在三角形的内部.符号语言：EFO 事实上，三角形的三条中线相交于一点. 我们把这三条中线的交点叫作三角形的重心. 如图，△ABC的三条中线AD，BE，CF相交于点G，则点G为△ABC的重心.G 例2 如图，AD是△ABC的中线，AE是△ABC的高.
（1）图中共有几个三角形？请分别列举出来.解 （1）图中有6个三角形，它们分别是：△ABD，△ADE，△AEC，△ABE，△ADC，△ABC.（2）其中哪些三角形的面积相等？解 因为AD是△ABC的中线，所以 BD=DC.因为AE是△ABC的高，也是△ABD和△ADC的高，所以S△ABD = S△ADC .2. 如图，AD是△ABC的高，DE是△ADB的中线，
BF是△EBD的角平分线，根据已知条件填空：ADC90AEABEBFDBE1、下列各个图形中，哪一个图形中AD是△ABC 的高( )2、填空：
（1）如图（1），AD，BE，CF是ΔABC的三条中线， 则 AB=2____ =2 ，BD= ，AE= 。AFBFDCAC（2）如图（2）， AD，BE，CF是ΔABC的三条角平分线，则
∠1= ， ∠3= ， ∠ACB=2 =2 。 ∠2∠ABC∠4∠ACF3.如图，在ΔABC中，AE是中线，AD是角平分线，AF是高。填空：
（1）BE= = ；
（2）∠BAD= = ；
（3）∠AFB= =90°；
（4）SΔABC= 。CEBE∠CAD∠BAC∠AFC课内训练4.如图在△ABC中∠ACE=∠BCE,BD=CD,则AD是三角形_____的_____线，CE是三角形_____的______线。5.如图，在三角形ABC中,BD是角平分线，BE是中线，如果AC=10cm,则AE=____cm,如果∠ABC=60°，则∠ABD=______6.如图在三角形ABC中，AD平分∠BAC,DE∥AC交AB于E点，若∠BAC=40°，则 ∠EDA=______ ABCDE7.能把三角形的面积平分的是三角形的______8.如图AD是△ABC的BC边上的中线，DE是△ADC的AC边上的中线，若△ABC面积等于4，则△ADE的面积等于_________ 。 练一练如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的?①AD是⊿ABE的角平分线 ( )②BE是⊿ABD边AD上的中线( )③BE是⊿ABC边AC上的中线( )④CH是⊿ACD边AD上的高 ( )三角形的高、中线与角平分线都是线段×××√拓展练习1.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是（ ）A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形B拓展练习2.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线D.以上三种性质合一
D拓展练习3.如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BD=EC
D.∠C的对边是DE
C4、判断：已知a+b>c，则以线段a、b、c为边能够成三角形。（ ）5、在ΔABC中，AB=9，BC=2，并且AC为奇数，那么ΔABC的周长为 。6、如图，已知BM是ΔABC的中线，AB=6，BC=8，那么ΔMBC的周长与ΔABM的周长相差 。?今天我们学了什么？1.三角形的高、中线、角平分线
的有关概念及它们的画法。2.三角形的高、中线、角平分线
的符号语言及简单应用。能力拓展
1.△ABC中，AB=AC,AD是中线，△ABC的周长为34cm,△ABD周长为30cm,，求AD的长。3、在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长. 1、三角形的一条中线是否将这个三角形分成面积相等的两个三角形?为什么? 2、如上图,已知:AD是BC边上的中线,BF为AD边上的中线,若△ABC的面积为4,则△ABD的面积为________, △ABF的面积为________.EF21补充例题补充例题 如图，在△ABC中，BP、CP分别是∠B、 ∠C的平分线，求证： ∠BPC= 90? + ∠A。BACP证明：∵BP、CP分别是∠B、 ∠C
的平分线(已知)∴∠1=∴∠2=( )角平分线定义∵ ∠BPC +∠1 + ∠2 =180?( 三角形内角和定理 )∠A +∠ABC +∠ACB=180?( 三角形内角和定理 )∴∠BPC=180??(∠1 +∠2 )现在做中考题（2010．昆明）如图，在△ABC中，CD是∠ACB的平分线，∠A = 80°，∠ACB=60°，那么∠BDC=（　）注意三角形的角平分线的应用 A．80° B．90°
C．100° D．110°D 2.如右图，AD是BC边上的高，BE是 △ ABD的角平分线，∠1=40°，∠2=30°，则∠C= ____∠BED= 。
3.如图所示:△ABC中,AD⊥BC于D, BE⊥AC于E, CF⊥AB于F,则△OBC的高是 。OF是哪些三角形的高？600650AD△ AOB, △ AOF, △ BOF