2.2 二次函数的图象与性质(第3课时) 课件 (共30张PPT)
文档属性
| 名称 | 2.2 二次函数的图象与性质(第3课时) 课件 (共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 19:13:36 | ||
图片预览








文档简介
(共30张PPT)
第二章 二次函数
2.2 二次函数的图象与性质
第3课时 二次函数y=a(x-h)2的图象与性质
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、熟练掌握二次函数y=a(x-h)2的图象与性质,学会画该二次函数的抛物线;
2、掌握二次函数y=a(x-h)2的对称轴、顶点坐标,并熟练掌握该函数的单调性;
导入新课
观察与思考
a,c的符号 a>0,c>0 a>0,c<0 a<0,c>0 a<0,c<0
图象
开口方向 对称轴 顶点坐标 函数的增减性 最值 向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
问题1 说说二次函数y=ax2+c(a≠0)的图象的特征.
讲授新课
知识点一 二次函数y=a(x-h)2的图象和性质
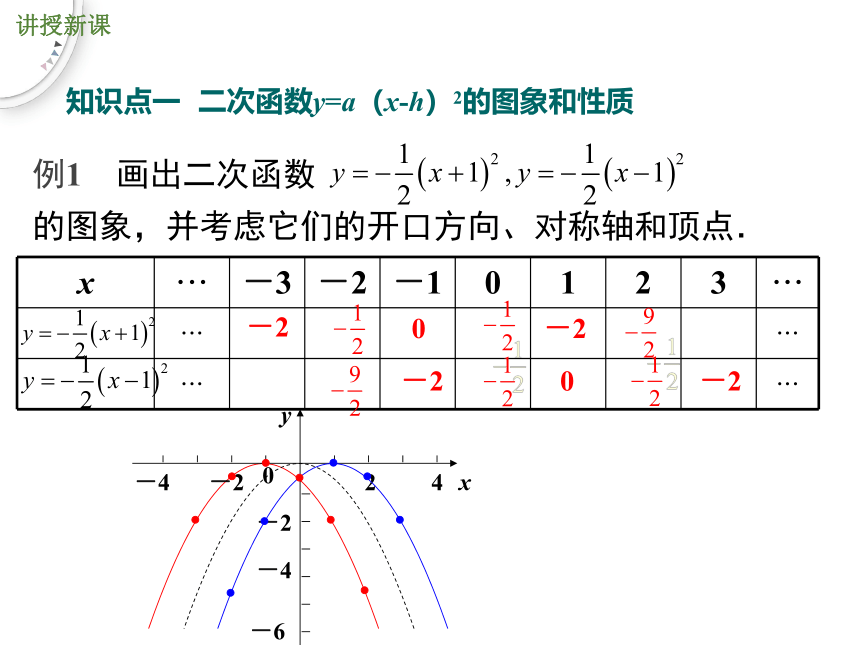
例1 画出二次函数 的图象,并考虑它们的开口方向、对称轴和顶点.
x ··· -3 -2 -1 0 1 2 3 ···
··· ···
··· ···
-2
-2
0
0
-2
-2
-2
2
-2
-4
-6
4
-4
0
x
y
x
y
O
-2
2
-2
-4
-6
4
-4
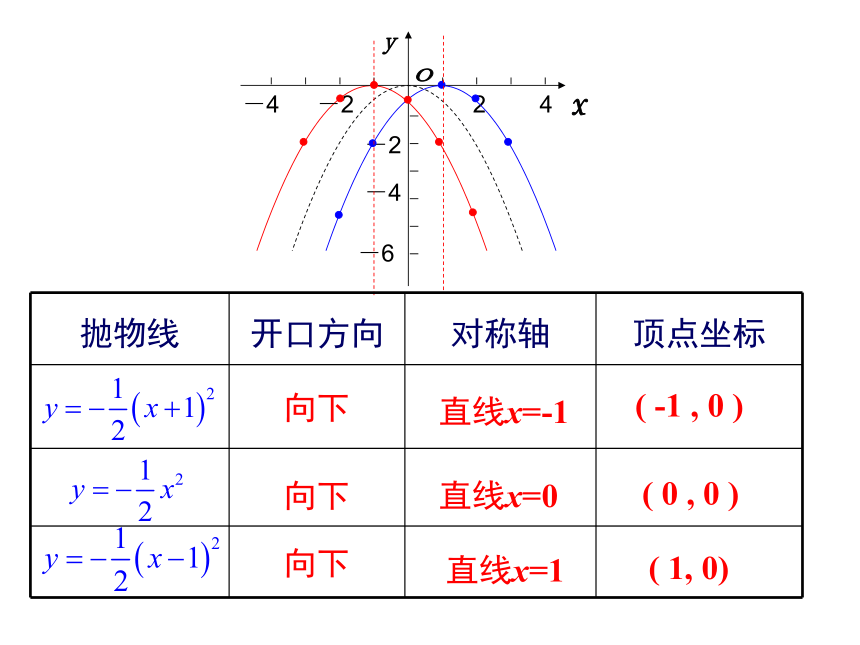
抛物线 开口方向 对称轴 顶点坐标
向下
直线x=-1
( -1 , 0 )
直线x=0
直线x=1
向下
向下
( 0 , 0 )
( 1, 0)
类似地,可以证明二次函数 y=a(x-h)2的下列性质
y=a(x-h)2 a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
直线x=h
直线x=h
(h,0)
(h,0)
当x=h时,y最小值=0
当x=h时,y最大值=0
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
例1 若抛物线y=3(x+ )2的图象上有三个点,A(-3 ,y1),B(-1,y2),C(0,y3),则y1,y2,y3的大小关系为________________.
解析:∵抛物线y=3(x+ )2的对称轴为x=- ,a=3>0,∴x<- 时,y随x的增大而减小;x>- 时,y随x的增大而增大.∵点A的坐标为(-3 ,y1),∴点A在抛物线上的对称点A′的坐标为( ,y1).∵- < 1<0< ,∴y2<y3<y1.故答案为y2<y3<y1.
典例精析
y2<y3<y1
知识点二 二次函数y=ax2的图象与y=a(x-h)2的图象的关系
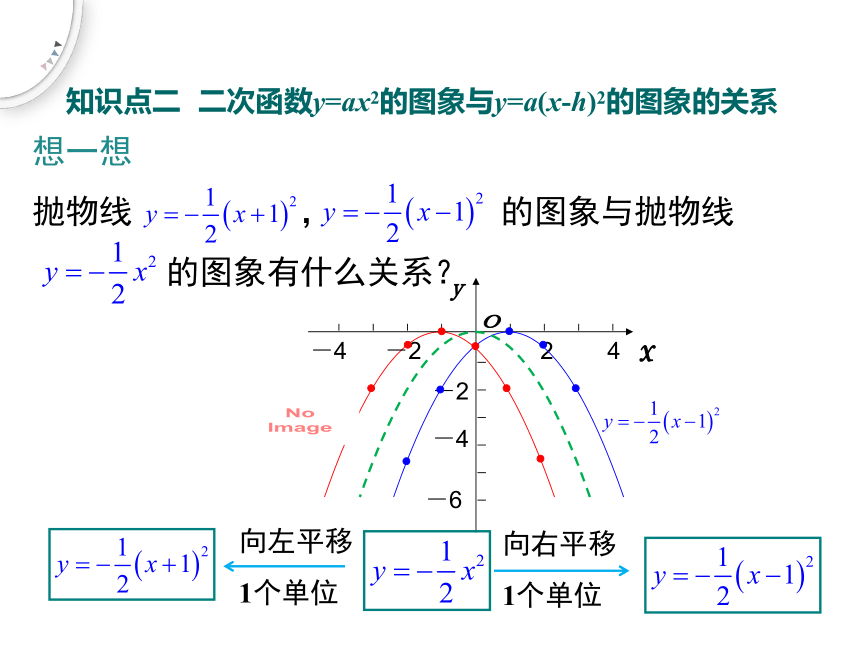
向右平移
1个单位
想一想
抛物线 , 的图象与抛物线
的图象有什么关系?
x
y
O
-2
2
-2
-4
-6
4
-4
向左平移
1个单位
知识要点
二次函数y=a(x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到(h>0).
左右平移规律:
括号内左加右减;括号外不变.
y=a(x-h)2
当向左平移 ︱h︱ 时
y=a(x+h)2
当向右平移 ︱h︱ 时
y=ax2
例2 抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
∴平移后二次函数关系式为y= (x-3)2.
方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
当堂练习
1.对于二次函数y=-2(x+3)2的图象,下列说法不正确的是( )
A.开口向下
B.对称轴是直线x=-3
C.顶点坐标为(-3,0)
D.当x<-3时,y随x的增大而减小
【答案】D
【详解】解:A、∵a=-2<0,
∴函数图象开口向下,故A正确,不符合题意;
B、对称轴是直线x=-3,故B正确,不符合题意;
C、顶点坐标为(-3,0),故C正确,不符合题意;
D、∵函数图象开口向下,对称轴是直线x=-3,
∴当x<-3时,y随x的增大而增大,故D不正确,符合题意;
故选:D.
2.对于二次函数y=-(x+2)2,下列结论中,错误的是( )
A.对称轴是直线x=-2
B.当x>-2时,y随x的增大而增大
C.当x=-2时,函数的最大值为0
D.开口向下
【答案】B
【分析】二次函数y=-(x+2)2是顶点式,结合它的图象顶点,开口方向,图象位置等,逐一判断.
【详解】解:根据二次函数的性质,可得:二次函数y=-(x+2)2的图象顶点为(-2,0),对称轴为x=-2,开口向下,
故当x=-2时,函数的最大值为0,当x>-2时,y随x的增大而减小;
故选:B.
3.如图,在平面直角坐标系中,抛物线y=(x-1)2与x轴只有一个交点M,与平行于x轴的直线l交于点A、B,若AB=4,则点M到直线l的距离为( )
A.2 B.3 C.4 D.5
【答案】C
【分析】设函数顶点坐标M为(h,0),点M到直线l的距离为a,则y=(x-h)2,再求出A、B坐标即可求解.
【详解】解:函数顶点坐标M为(h,0),点M到直线l的距离为a,
则:y=(x-h)2=a,解得:x=h±,
即:A(h﹣,0),B(h+,0),
∵AB=4,
∴h+﹣(h﹣)=4,解得:a=4.
故选:C.
4.已知二次函数y=-2(x+b)2,当x<-3时,y随x的增大而增大,当x>-3时,y随x的增大而减小,则当x=1时,y的值为( )
A.-12 B.12 C.32 D.-32
【答案】D
【分析】根据当x<-3时,y随x的增大而增大,当x>-3时,y随x的增大而减小,即可得到抛物线的对称轴为直线x=-3,由此求解即可.
【详解】解:∵当x<-3时,y随x的增大而增大,当x>-3时,y随x的增大而减小,
∴抛物线的对称轴为直线下,
∴b=3,
∴当x=1时,y=-32,
故选D.
5.抛物线y=-3(x+8)2的顶点坐标是 _____.
【答案】(-8,0)
【分析】由二次函数解析式的顶点式,可得抛物线顶点坐标.
【详解】解:∵y=-2(x+8)2,
∴抛物线顶点坐标为(-8,0),
故答案为:(-8,0).
6.若点A(-2,y1),B(2,y2)在抛物线y=(x+1)2上,则y1与y2的大小关系为:y1_________y2(填“>”,“=”或“<”).
【答案】<
【分析】利用二次函数图象上点的坐标特征可得出y1,y2的值,比较后即可得出结论.
【详解】解:∵若点A(-2,y1),B(2,y2)在抛物线y=(x+1)2上,
∴y1=1,y2=9
∵1<9,
∴y1<y2.
故答案为:<.
7.在平面直角坐标系内有线段PQ,已知P(3,1)、Q(9,1),若抛物线y=(x-a)2与线段PQ有交点,则a 的取值范围是______.
【答案】2≤a≤10
【点睛】本题考查了抛物线的图象与性质,掌握抛物线随值的变化左右移动是解题的关键.
8.已知抛物线y=a(x-2)2+1与x轴有两个交点,把该抛物线向下平移m个单位长度得到新抛物线与x轴没有交点,则m的值可以是___________.(只填一个符合题意的值即可)
【答案】2(答案不唯一)
【分析】先根据抛物线y=a(x-2)2+1与x轴有两个交点,得出a<0,然后写出平移后的抛物线解析式为y=a(x-2)2+1-m,根据新抛物线与x轴没有交点,得出1-m<0,再求解即可.
【详解】∵抛物线y=a(x-2)2+1与x轴有两个交点,
∴抛物线开口向下,即a<0,
∴抛物线向下平移m个单位长度后,新抛物线解析式为y=a(x-2)2+1-m,
∵新抛物线与x轴没有交点,
∴1-m<0,
∴m>1,
取符合题意的m的值为2(答案不唯一).
故答案为:2(答案不唯一)
9.已知抛物线y=(x-2)2经过点A(-2,b).
(1)求b的值;
(2)判断点B(10,8)是否在此抛物线上?
【答案】(1)16
(2)不在
【详解】(1)解:抛物线y=(x-2)2经过点A(-2,b),
∴b=(-2-2)2=16;
(2)解:∵当x=10时,y=64≠8,
∴B(10,8)不在此抛物线上.
10.已知二次函数y=x2-6x+8.
(1)将解析式化成顶点式;
(2)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.
【答案】(1)y=(x-3)2-1;(2)x≥3,x≤3.
【分析】(1)对解析式进行配方即可得顶点式;
(2)根据顶点式可以确定对称轴,进而可确定函数的增减性.
【详解】(1)y=x2-6x+8=x2-6x+9-1=(x-3)2-1;
(2)由(1)可知二次函数开口向上,对称轴为x=3,
∴当x≥3时,y随x的增大而增大;x≤3时,y随x增大而减小.
课堂小结
平移规律:
括号内:左加右减;括号外不变.
复习y=ax2+k
探索y=a(x-h)2的图象及性质
图象的画法
图象的特征
描点法
平移法
开口方向及增减性
顶点坐标
对称轴
平移关系
直线x=h
(h,0)
a>0,开口向上
a<0,开口向下
a的符号决定
增减性
y=ax2
第二章 二次函数
2.2 二次函数的图象与性质
第3课时 二次函数y=a(x-h)2的图象与性质
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、熟练掌握二次函数y=a(x-h)2的图象与性质,学会画该二次函数的抛物线;
2、掌握二次函数y=a(x-h)2的对称轴、顶点坐标,并熟练掌握该函数的单调性;
导入新课
观察与思考
a,c的符号 a>0,c>0 a>0,c<0 a<0,c>0 a<0,c<0
图象
开口方向 对称轴 顶点坐标 函数的增减性 最值 向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
问题1 说说二次函数y=ax2+c(a≠0)的图象的特征.
讲授新课
知识点一 二次函数y=a(x-h)2的图象和性质
例1 画出二次函数 的图象,并考虑它们的开口方向、对称轴和顶点.
x ··· -3 -2 -1 0 1 2 3 ···
··· ···
··· ···
-2
-2
0
0
-2
-2
-2
2
-2
-4
-6
4
-4
0
x
y
x
y
O
-2
2
-2
-4
-6
4
-4
抛物线 开口方向 对称轴 顶点坐标
向下
直线x=-1
( -1 , 0 )
直线x=0
直线x=1
向下
向下
( 0 , 0 )
( 1, 0)
类似地,可以证明二次函数 y=a(x-h)2的下列性质
y=a(x-h)2 a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
直线x=h
直线x=h
(h,0)
(h,0)
当x=h时,y最小值=0
当x=h时,y最大值=0
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
例1 若抛物线y=3(x+ )2的图象上有三个点,A(-3 ,y1),B(-1,y2),C(0,y3),则y1,y2,y3的大小关系为________________.
解析:∵抛物线y=3(x+ )2的对称轴为x=- ,a=3>0,∴x<- 时,y随x的增大而减小;x>- 时,y随x的增大而增大.∵点A的坐标为(-3 ,y1),∴点A在抛物线上的对称点A′的坐标为( ,y1).∵- < 1<0< ,∴y2<y3<y1.故答案为y2<y3<y1.
典例精析
y2<y3<y1
知识点二 二次函数y=ax2的图象与y=a(x-h)2的图象的关系
向右平移
1个单位
想一想
抛物线 , 的图象与抛物线
的图象有什么关系?
x
y
O
-2
2
-2
-4
-6
4
-4
向左平移
1个单位
知识要点
二次函数y=a(x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到(h>0).
左右平移规律:
括号内左加右减;括号外不变.
y=a(x-h)2
当向左平移 ︱h︱ 时
y=a(x+h)2
当向右平移 ︱h︱ 时
y=ax2
例2 抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
∴平移后二次函数关系式为y= (x-3)2.
方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
当堂练习
1.对于二次函数y=-2(x+3)2的图象,下列说法不正确的是( )
A.开口向下
B.对称轴是直线x=-3
C.顶点坐标为(-3,0)
D.当x<-3时,y随x的增大而减小
【答案】D
【详解】解:A、∵a=-2<0,
∴函数图象开口向下,故A正确,不符合题意;
B、对称轴是直线x=-3,故B正确,不符合题意;
C、顶点坐标为(-3,0),故C正确,不符合题意;
D、∵函数图象开口向下,对称轴是直线x=-3,
∴当x<-3时,y随x的增大而增大,故D不正确,符合题意;
故选:D.
2.对于二次函数y=-(x+2)2,下列结论中,错误的是( )
A.对称轴是直线x=-2
B.当x>-2时,y随x的增大而增大
C.当x=-2时,函数的最大值为0
D.开口向下
【答案】B
【分析】二次函数y=-(x+2)2是顶点式,结合它的图象顶点,开口方向,图象位置等,逐一判断.
【详解】解:根据二次函数的性质,可得:二次函数y=-(x+2)2的图象顶点为(-2,0),对称轴为x=-2,开口向下,
故当x=-2时,函数的最大值为0,当x>-2时,y随x的增大而减小;
故选:B.
3.如图,在平面直角坐标系中,抛物线y=(x-1)2与x轴只有一个交点M,与平行于x轴的直线l交于点A、B,若AB=4,则点M到直线l的距离为( )
A.2 B.3 C.4 D.5
【答案】C
【分析】设函数顶点坐标M为(h,0),点M到直线l的距离为a,则y=(x-h)2,再求出A、B坐标即可求解.
【详解】解:函数顶点坐标M为(h,0),点M到直线l的距离为a,
则:y=(x-h)2=a,解得:x=h±,
即:A(h﹣,0),B(h+,0),
∵AB=4,
∴h+﹣(h﹣)=4,解得:a=4.
故选:C.
4.已知二次函数y=-2(x+b)2,当x<-3时,y随x的增大而增大,当x>-3时,y随x的增大而减小,则当x=1时,y的值为( )
A.-12 B.12 C.32 D.-32
【答案】D
【分析】根据当x<-3时,y随x的增大而增大,当x>-3时,y随x的增大而减小,即可得到抛物线的对称轴为直线x=-3,由此求解即可.
【详解】解:∵当x<-3时,y随x的增大而增大,当x>-3时,y随x的增大而减小,
∴抛物线的对称轴为直线下,
∴b=3,
∴当x=1时,y=-32,
故选D.
5.抛物线y=-3(x+8)2的顶点坐标是 _____.
【答案】(-8,0)
【分析】由二次函数解析式的顶点式,可得抛物线顶点坐标.
【详解】解:∵y=-2(x+8)2,
∴抛物线顶点坐标为(-8,0),
故答案为:(-8,0).
6.若点A(-2,y1),B(2,y2)在抛物线y=(x+1)2上,则y1与y2的大小关系为:y1_________y2(填“>”,“=”或“<”).
【答案】<
【分析】利用二次函数图象上点的坐标特征可得出y1,y2的值,比较后即可得出结论.
【详解】解:∵若点A(-2,y1),B(2,y2)在抛物线y=(x+1)2上,
∴y1=1,y2=9
∵1<9,
∴y1<y2.
故答案为:<.
7.在平面直角坐标系内有线段PQ,已知P(3,1)、Q(9,1),若抛物线y=(x-a)2与线段PQ有交点,则a 的取值范围是______.
【答案】2≤a≤10
【点睛】本题考查了抛物线的图象与性质,掌握抛物线随值的变化左右移动是解题的关键.
8.已知抛物线y=a(x-2)2+1与x轴有两个交点,把该抛物线向下平移m个单位长度得到新抛物线与x轴没有交点,则m的值可以是___________.(只填一个符合题意的值即可)
【答案】2(答案不唯一)
【分析】先根据抛物线y=a(x-2)2+1与x轴有两个交点,得出a<0,然后写出平移后的抛物线解析式为y=a(x-2)2+1-m,根据新抛物线与x轴没有交点,得出1-m<0,再求解即可.
【详解】∵抛物线y=a(x-2)2+1与x轴有两个交点,
∴抛物线开口向下,即a<0,
∴抛物线向下平移m个单位长度后,新抛物线解析式为y=a(x-2)2+1-m,
∵新抛物线与x轴没有交点,
∴1-m<0,
∴m>1,
取符合题意的m的值为2(答案不唯一).
故答案为:2(答案不唯一)
9.已知抛物线y=(x-2)2经过点A(-2,b).
(1)求b的值;
(2)判断点B(10,8)是否在此抛物线上?
【答案】(1)16
(2)不在
【详解】(1)解:抛物线y=(x-2)2经过点A(-2,b),
∴b=(-2-2)2=16;
(2)解:∵当x=10时,y=64≠8,
∴B(10,8)不在此抛物线上.
10.已知二次函数y=x2-6x+8.
(1)将解析式化成顶点式;
(2)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.
【答案】(1)y=(x-3)2-1;(2)x≥3,x≤3.
【分析】(1)对解析式进行配方即可得顶点式;
(2)根据顶点式可以确定对称轴,进而可确定函数的增减性.
【详解】(1)y=x2-6x+8=x2-6x+9-1=(x-3)2-1;
(2)由(1)可知二次函数开口向上,对称轴为x=3,
∴当x≥3时,y随x的增大而增大;x≤3时,y随x增大而减小.
课堂小结
平移规律:
括号内:左加右减;括号外不变.
复习y=ax2+k
探索y=a(x-h)2的图象及性质
图象的画法
图象的特征
描点法
平移法
开口方向及增减性
顶点坐标
对称轴
平移关系
直线x=h
(h,0)
a>0,开口向上
a<0,开口向下
a的符号决定
增减性
y=ax2
