3.9 弧长和扇形面积 课件 (共19张PPT)
文档属性
| 名称 | 3.9 弧长和扇形面积 课件 (共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
数学(北师大版)
九年级 下册
3.9 弧长及扇形面积
第三章 圆
课前导入
学习目标
1.理解弧长和扇形面积公式的推导过程。
2.灵活运用弧长及扇形面积公式解决实际问题。
重点
理解弧长和扇形面积公式的推导过程。
难点
利用弧长和扇形面积公式进行计算。
情景引入
在运动会的200米比赛中,为什么他们的起跑线不在同一处?
因为不同的跑道,跑道一圈的长度不一样,要保证这些弯道的“展直长度”是一样的,所以运动员的起跑线不在同一处,越靠近外侧的运动员所在跑道的长度越长,所以他的起跑位置越靠前。
本节课我们学习如何计算弯道的“展直长度”。
探索与思考
O
●
C
D
A
B
A
B
1°的圆心角
1°的弧
C
D
n°的圆心角
n°的弧
圆心角的度数与它所对的弧的度数相等。
如何将⊙O的圆周分为360等份
探索与思考
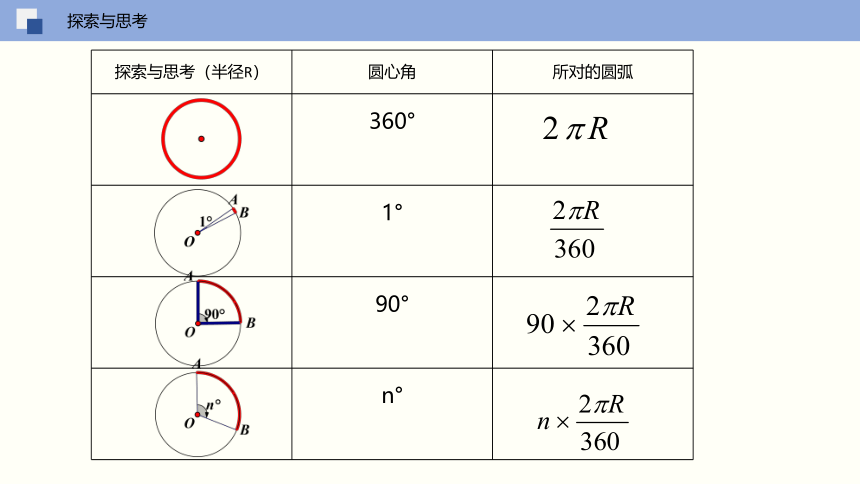
探索与思考(半径R) 圆心角 所对的圆弧
360°
1°
90°
n°
弧长公式
在半径为R的圆中,n°的圆心角所对弧长的计算公式为:
说明:
1)n没有单位,弧长和半径单位一致。
2)弧长的大小与圆心角大小和半径的长度有关。
3)弧长公式变形
,R、n、l三个量,已知两个可求另一个。
4)扇形周长公式=2R+l=2R+
课堂基础练
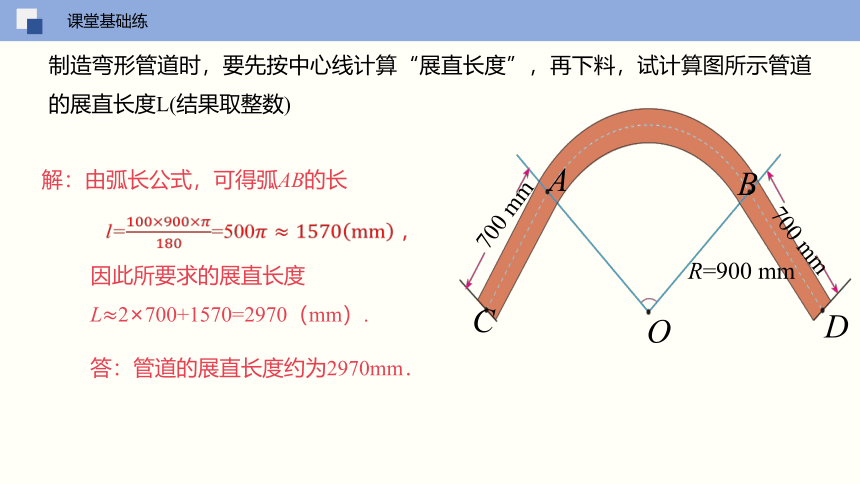
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(结果取整数)
A
B
C
D
O
R=900 mm
700 mm
700 mm
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
L≈2×700+1570=2970(mm).
答:管道的展直长度约为2970mm.
扇形面积
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
扇形的概念:
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
如何求扇形的面积?
探索与思考
探索与思考(半径R) 圆心角 扇形面积
360°
1°
90°
n°
扇形面积公式
扇形的面积公式:半径为R,圆心角为n°的扇形的面积是
说明:扇形面积公式中的“n”和弧长公式中的“n”一样,表示“1°”的圆心角的倍数,参与计算时不带单位。
探索与思考
比较弧长公式和扇形面积公式,你能发现它们的异同点吗?
课堂基础练
1.75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是( )
A.6cm B.7cm C.8cm D.9cm
2.在半径为6 cm的圆中,长为2π cm的弧所对的圆周角的度数为 ( )
A.30° B.45° C.60° D.90°
【详解】解:∵75°的圆心角所对的弧长是2.5πcm,
由弧长公式l,∴2.5π,解得:r=6,故选:A.
【详解】∵,
∴圆心角的度数为n=2×30°=60°.
∴长为2π cm的弧所对的圆周角的度数为,
故选A.
课堂基础练
【详解】解:设这个扇形的半径为r,圆心角是n,面积为S,弧长为l,
由题意得:,即240π=×20πr,解得:r=24,
又由可得:,解得:,故选:B.
3.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角是( )
A.120° B.150° C.60° D.100°
4.(2021·四川成都·中考真题)如图,正六边形的边长为6,以顶点A为圆心,的长为半径画圆,则图中阴影部分的面积为( )
A. B. C. D.
【详解】解:∵六边形ABCDEF是正六边形,
∴∠FAB=,AB=6,
∴扇形ABF的面积=12π,故选择D.
随堂测试
1.如图,扇形纸扇完全打开后,扇面(即扇形ABC)的面积为cm2,竹条AB,AC的长均为18 cm,D,E分别为AB,AC的中点,则 的长为( )
A.cm B.7πcm C.cm D.cm
【详解】,D,E分别为AB,AC的中点,
,
扇面(即扇形ABC)的面积为cm2,
,
解得,
∠ABC=150°,
,
故选:C.
随堂测试
2.某款“不倒翁”(图1)的主视图是图2,PA,PB分别与所在圆相切于点A,B.若该圆半径是9cm,∠P=40°,则的长是( )
A.cm B.cm C. cm D.cm
【详解】解:如图,
PA,PB分别与所在圆相切于点A,B.
∠PAO=∠PBO=90°
∠P=40°,
,
该圆半径是9cm,
cm,
故选:A.
随堂测试
3.如图,小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的圆心角为216°,面积是15πcm2,那么这个圆锥的底面半径是( )
A.2cm B.3cm C.4cm D.5cm
【详解】解:设扇形的半径为r,根据题意得:
,解得:,
∴扇形的弧长为,
∴这个圆锥的底面半径是.
故选:B
随堂测试
4.如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
A.πm2 B.πm2 C.πm2 D.πm2
【详解】解:大扇形的圆心角是90度,半径是5m,
所以面积= =π(m2);
小扇形的圆心角是180°﹣120°=60°,半径是1m,
则面积==(m2),
则小羊A在草地上的最大活动区域面积=π+=π(m2).
故选: B.
随堂测试
5.(2019·广东·中考真题)在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点,的三个顶点均在格点上,以点为圆心的与相切于点,分别交、于点、.
(1)求三边的长;
(2)求图中由线段、、及所围成的阴影部分的面积.
【详解】(1),,
;
(2)由(1)得AB2+BC2=(2)2+(2)2=80=(4)2=BC2,∴,
连接,则,
∴===.
谢谢~
数学(北师大版)
九年级 下册
3.9 弧长及扇形面积
第三章 圆
课前导入
学习目标
1.理解弧长和扇形面积公式的推导过程。
2.灵活运用弧长及扇形面积公式解决实际问题。
重点
理解弧长和扇形面积公式的推导过程。
难点
利用弧长和扇形面积公式进行计算。
情景引入
在运动会的200米比赛中,为什么他们的起跑线不在同一处?
因为不同的跑道,跑道一圈的长度不一样,要保证这些弯道的“展直长度”是一样的,所以运动员的起跑线不在同一处,越靠近外侧的运动员所在跑道的长度越长,所以他的起跑位置越靠前。
本节课我们学习如何计算弯道的“展直长度”。
探索与思考
O
●
C
D
A
B
A
B
1°的圆心角
1°的弧
C
D
n°的圆心角
n°的弧
圆心角的度数与它所对的弧的度数相等。
如何将⊙O的圆周分为360等份
探索与思考
探索与思考(半径R) 圆心角 所对的圆弧
360°
1°
90°
n°
弧长公式
在半径为R的圆中,n°的圆心角所对弧长的计算公式为:
说明:
1)n没有单位,弧长和半径单位一致。
2)弧长的大小与圆心角大小和半径的长度有关。
3)弧长公式变形
,R、n、l三个量,已知两个可求另一个。
4)扇形周长公式=2R+l=2R+
课堂基础练
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(结果取整数)
A
B
C
D
O
R=900 mm
700 mm
700 mm
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
L≈2×700+1570=2970(mm).
答:管道的展直长度约为2970mm.
扇形面积
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
扇形的概念:
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
如何求扇形的面积?
探索与思考
探索与思考(半径R) 圆心角 扇形面积
360°
1°
90°
n°
扇形面积公式
扇形的面积公式:半径为R,圆心角为n°的扇形的面积是
说明:扇形面积公式中的“n”和弧长公式中的“n”一样,表示“1°”的圆心角的倍数,参与计算时不带单位。
探索与思考
比较弧长公式和扇形面积公式,你能发现它们的异同点吗?
课堂基础练
1.75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是( )
A.6cm B.7cm C.8cm D.9cm
2.在半径为6 cm的圆中,长为2π cm的弧所对的圆周角的度数为 ( )
A.30° B.45° C.60° D.90°
【详解】解:∵75°的圆心角所对的弧长是2.5πcm,
由弧长公式l,∴2.5π,解得:r=6,故选:A.
【详解】∵,
∴圆心角的度数为n=2×30°=60°.
∴长为2π cm的弧所对的圆周角的度数为,
故选A.
课堂基础练
【详解】解:设这个扇形的半径为r,圆心角是n,面积为S,弧长为l,
由题意得:,即240π=×20πr,解得:r=24,
又由可得:,解得:,故选:B.
3.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角是( )
A.120° B.150° C.60° D.100°
4.(2021·四川成都·中考真题)如图,正六边形的边长为6,以顶点A为圆心,的长为半径画圆,则图中阴影部分的面积为( )
A. B. C. D.
【详解】解:∵六边形ABCDEF是正六边形,
∴∠FAB=,AB=6,
∴扇形ABF的面积=12π,故选择D.
随堂测试
1.如图,扇形纸扇完全打开后,扇面(即扇形ABC)的面积为cm2,竹条AB,AC的长均为18 cm,D,E分别为AB,AC的中点,则 的长为( )
A.cm B.7πcm C.cm D.cm
【详解】,D,E分别为AB,AC的中点,
,
扇面(即扇形ABC)的面积为cm2,
,
解得,
∠ABC=150°,
,
故选:C.
随堂测试
2.某款“不倒翁”(图1)的主视图是图2,PA,PB分别与所在圆相切于点A,B.若该圆半径是9cm,∠P=40°,则的长是( )
A.cm B.cm C. cm D.cm
【详解】解:如图,
PA,PB分别与所在圆相切于点A,B.
∠PAO=∠PBO=90°
∠P=40°,
,
该圆半径是9cm,
cm,
故选:A.
随堂测试
3.如图,小明用图中的扇形纸片作一个圆锥的侧面,已知扇形的圆心角为216°,面积是15πcm2,那么这个圆锥的底面半径是( )
A.2cm B.3cm C.4cm D.5cm
【详解】解:设扇形的半径为r,根据题意得:
,解得:,
∴扇形的弧长为,
∴这个圆锥的底面半径是.
故选:B
随堂测试
4.如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
A.πm2 B.πm2 C.πm2 D.πm2
【详解】解:大扇形的圆心角是90度,半径是5m,
所以面积= =π(m2);
小扇形的圆心角是180°﹣120°=60°,半径是1m,
则面积==(m2),
则小羊A在草地上的最大活动区域面积=π+=π(m2).
故选: B.
随堂测试
5.(2019·广东·中考真题)在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点,的三个顶点均在格点上,以点为圆心的与相切于点,分别交、于点、.
(1)求三边的长;
(2)求图中由线段、、及所围成的阴影部分的面积.
【详解】(1),,
;
(2)由(1)得AB2+BC2=(2)2+(2)2=80=(4)2=BC2,∴,
连接,则,
∴===.
谢谢~
