3.8 圆内接正多边形 课件 (共17张PPT)
文档属性
| 名称 | 3.8 圆内接正多边形 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 19:33:25 | ||
图片预览





文档简介
(共17张PPT)
数学(北师大版)
九年级 下册
3.8 圆内接正多边形
第三章 圆
课前导入
学习目标
1.了解正多边形和圆的有关概念。
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系。
3.画圆内接正多边形。
重点
正多边形的概念及正多边形与圆的关系。
难点
利用直尺和圆规画特殊的正多边形。
情景引入
观察下面正多边形,你发现了什么?
正多边形的顶点都在圆上
圆内接正多边形的相关概念
O
A
D
C
B
正多边形的中心:一个正多边形的外接圆的圆心。
正多边形的半径:外接圆的半径。
正多边形的中心角:正多边形的每一条边所对的圆心角。
正多边形的边心距:中心到正多边形一边的距离。
半径r
中心角
边心距
E
把一个圆分成相等的n(n≥3)段弧,依次连接各分点所得多边形就是这个圆的内接正多边形,这个圆就是这个正多边形的外接圆。
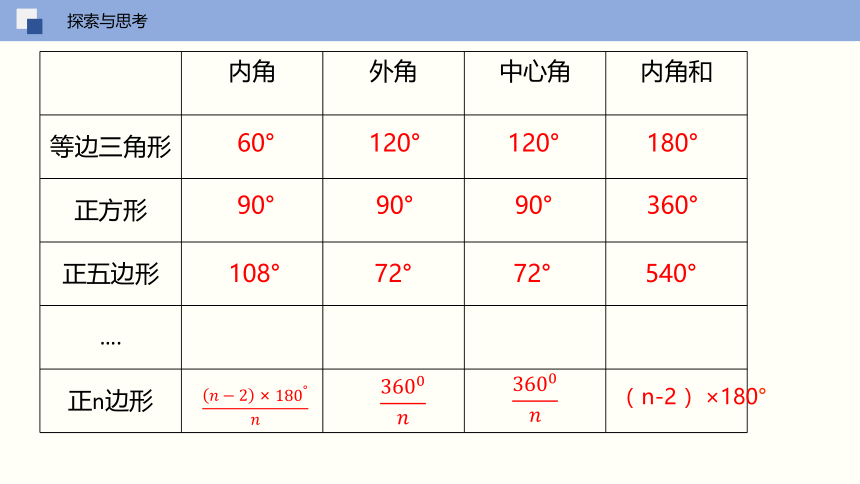
探索与思考
内角 外角 中心角 内角和
等边三角形
正方形
正五边形
….
正n边形
60°
120°
120°
90°
90°
90°
108°
72°
72°
180°
360°
540°
( n-2 )×180°
探索与思考
正n边形的一个内角的度数是____________;
中心角是___________;
正多边形的中心角与外角的大小关系是________.
相等
E
D
C
B
A
O
F
课堂基础练
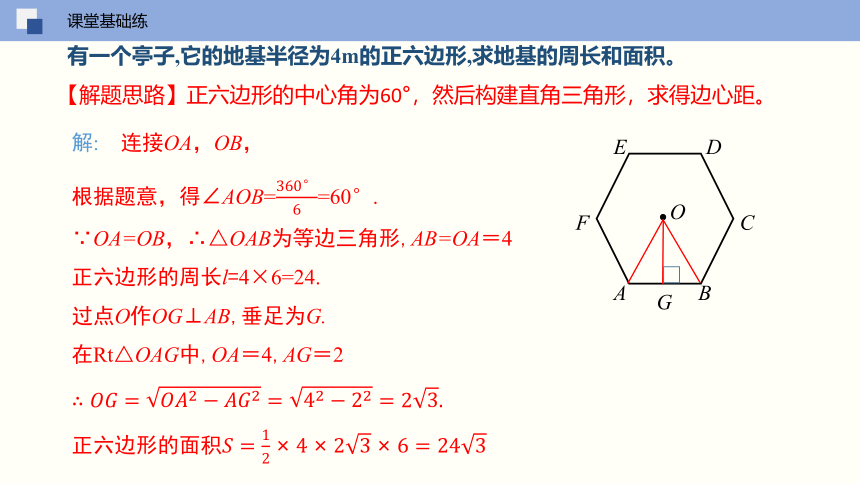
有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积。
【解题思路】正六边形的中心角为60°,然后构建直角三角形,求得边心距。
解: 连接OA,OB,
根据题意,得∠AOB==60°.
∵OA=OB,∴△OAB为等边三角形,AB=OA=4
正六边形的周长l=4×6=24.
过点O作OG⊥AB,垂足为G.
在Rt△OAG中,OA=4,AG=2
正六边形的面积
E
A
B
C
D
F
O
G
随堂测试
1.若一个正多边形的中心角为40°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
【详解】解:设这个正多边形的边数是n,由题意得:,解得:n=9,故选A.
2.半径为2cm的圆内接正六边形的面积等于( )
A.4 B.5 C. D.6
【详解】如图:
求半径为2cm的圆内接正六边形的面积等于求六个与该圆半径为边长的六个等边三角形的面积,
∴该面积为:,
故选:C.
随堂测试
3.如图,已知正六边形的边心距为3,则它的周长是( )
A.6 B.12 C. D.
【详解】解:如图,过点作于点,由题意得:边心距,
六边形是正六边形,,
是等边三角形,,
,,解得,
则正六边形的周长为,
故选:D.
随堂测试
4.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角=____,边长=____,边心距=____.
【详解】解:在圆内接正六边形ABCDEF中,∠COD=,
又∵OC=OD=4,∴△OCD是等边三角形,∴BC=CD=OC=4,
∵OG⊥BC,∴CG=BC=2,
∴边心距:,
随堂测试
5.如图,AC、AD为正六边形ABCDEF的两条对角线,若该正六边形的边长为2,则△ACD的周长为 _____.
【详解】解:∵正六边形ABCDEF,
∴∠B=∠BCD120°,AB=BC,
∴∠ACB=∠BCA=30°,
∴∠ACD=120°﹣30°=90°,
由对称性可得,AD是正六边形的对称轴,
∴∠ADC=∠ADE∠CDE=60°,
在Rt△ACD中,CD=2,∠ADC=60°,
∴AD=2CD=4,ACCD=2,
∴△ACD的周长为AC+CD+AD=22+4=26
随堂测试
6.一个正多边形的周长为60,边长为a,一个外角为b°.
1)若a=6,求b的值;
2)若b=30,求a的值.
(1)解:∵正多边形的周长为60,边长为6,∴边数为,
∵一个外角为b°,∴;
(2)∵一个外角为b°,b=30,∴,
∵正多边形的周长为60,边长为a,∴.
探索与思考
如何把一个圆分成相等的一些弧,并画出这个圆的内接正多边形?
方法一:用量角器等分圆周
用量角器等分圆方法: 由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形。采用“先用量角器画一个 的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”。
【优缺点】方法简便且可以画任意正多边形、误差小。
方法二 用尺规等分圆周
用尺规等分圆方法:用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形。
【优缺点】这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差。
探索与思考
方法简述:正五边形的中心角为72°,通过量角器量取72°,通过圆规依次截取等长弧,画图。
(量角器+圆规)
尝试画出圆内接正三角形、正方形、正五边形、正八边形?
等边三角形
正五边形
120°
120°
120°
方法简述:等边三角形的中心角为120°,通过量角器依次量取120°,画图。(量角器)
72°
探索与思考
尝试画出圆内接正三角形、正方形、正五边形、正八边形?
正方形
正八边形
45°
课堂基础练
尝试画出圆内接正六边形?
作法:1)在⊙O中任意作一条直径AD.
2)分别以点A、D为圆心,⊙O的半径为半径作弧,与⊙O相交于点B、F和点C、E.
3)依次连接A、B、C、D、E、F各点.
正六边形ABCDEF就是所求作的正六边形.
O
A
B
C
F
D
E
谢谢~
数学(北师大版)
九年级 下册
3.8 圆内接正多边形
第三章 圆
课前导入
学习目标
1.了解正多边形和圆的有关概念。
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系。
3.画圆内接正多边形。
重点
正多边形的概念及正多边形与圆的关系。
难点
利用直尺和圆规画特殊的正多边形。
情景引入
观察下面正多边形,你发现了什么?
正多边形的顶点都在圆上
圆内接正多边形的相关概念
O
A
D
C
B
正多边形的中心:一个正多边形的外接圆的圆心。
正多边形的半径:外接圆的半径。
正多边形的中心角:正多边形的每一条边所对的圆心角。
正多边形的边心距:中心到正多边形一边的距离。
半径r
中心角
边心距
E
把一个圆分成相等的n(n≥3)段弧,依次连接各分点所得多边形就是这个圆的内接正多边形,这个圆就是这个正多边形的外接圆。
探索与思考
内角 外角 中心角 内角和
等边三角形
正方形
正五边形
….
正n边形
60°
120°
120°
90°
90°
90°
108°
72°
72°
180°
360°
540°
( n-2 )×180°
探索与思考
正n边形的一个内角的度数是____________;
中心角是___________;
正多边形的中心角与外角的大小关系是________.
相等
E
D
C
B
A
O
F
课堂基础练
有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积。
【解题思路】正六边形的中心角为60°,然后构建直角三角形,求得边心距。
解: 连接OA,OB,
根据题意,得∠AOB==60°.
∵OA=OB,∴△OAB为等边三角形,AB=OA=4
正六边形的周长l=4×6=24.
过点O作OG⊥AB,垂足为G.
在Rt△OAG中,OA=4,AG=2
正六边形的面积
E
A
B
C
D
F
O
G
随堂测试
1.若一个正多边形的中心角为40°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
【详解】解:设这个正多边形的边数是n,由题意得:,解得:n=9,故选A.
2.半径为2cm的圆内接正六边形的面积等于( )
A.4 B.5 C. D.6
【详解】如图:
求半径为2cm的圆内接正六边形的面积等于求六个与该圆半径为边长的六个等边三角形的面积,
∴该面积为:,
故选:C.
随堂测试
3.如图,已知正六边形的边心距为3,则它的周长是( )
A.6 B.12 C. D.
【详解】解:如图,过点作于点,由题意得:边心距,
六边形是正六边形,,
是等边三角形,,
,,解得,
则正六边形的周长为,
故选:D.
随堂测试
4.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角=____,边长=____,边心距=____.
【详解】解:在圆内接正六边形ABCDEF中,∠COD=,
又∵OC=OD=4,∴△OCD是等边三角形,∴BC=CD=OC=4,
∵OG⊥BC,∴CG=BC=2,
∴边心距:,
随堂测试
5.如图,AC、AD为正六边形ABCDEF的两条对角线,若该正六边形的边长为2,则△ACD的周长为 _____.
【详解】解:∵正六边形ABCDEF,
∴∠B=∠BCD120°,AB=BC,
∴∠ACB=∠BCA=30°,
∴∠ACD=120°﹣30°=90°,
由对称性可得,AD是正六边形的对称轴,
∴∠ADC=∠ADE∠CDE=60°,
在Rt△ACD中,CD=2,∠ADC=60°,
∴AD=2CD=4,ACCD=2,
∴△ACD的周长为AC+CD+AD=22+4=26
随堂测试
6.一个正多边形的周长为60,边长为a,一个外角为b°.
1)若a=6,求b的值;
2)若b=30,求a的值.
(1)解:∵正多边形的周长为60,边长为6,∴边数为,
∵一个外角为b°,∴;
(2)∵一个外角为b°,b=30,∴,
∵正多边形的周长为60,边长为a,∴.
探索与思考
如何把一个圆分成相等的一些弧,并画出这个圆的内接正多边形?
方法一:用量角器等分圆周
用量角器等分圆方法: 由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形。采用“先用量角器画一个 的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”。
【优缺点】方法简便且可以画任意正多边形、误差小。
方法二 用尺规等分圆周
用尺规等分圆方法:用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形。
【优缺点】这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差。
探索与思考
方法简述:正五边形的中心角为72°,通过量角器量取72°,通过圆规依次截取等长弧,画图。
(量角器+圆规)
尝试画出圆内接正三角形、正方形、正五边形、正八边形?
等边三角形
正五边形
120°
120°
120°
方法简述:等边三角形的中心角为120°,通过量角器依次量取120°,画图。(量角器)
72°
探索与思考
尝试画出圆内接正三角形、正方形、正五边形、正八边形?
正方形
正八边形
45°
课堂基础练
尝试画出圆内接正六边形?
作法:1)在⊙O中任意作一条直径AD.
2)分别以点A、D为圆心,⊙O的半径为半径作弧,与⊙O相交于点B、F和点C、E.
3)依次连接A、B、C、D、E、F各点.
正六边形ABCDEF就是所求作的正六边形.
O
A
B
C
F
D
E
谢谢~
