3.6 直线与圆的位置关系(第二课时) 课件 (共19张PPT)
文档属性
| 名称 | 3.6 直线与圆的位置关系(第二课时) 课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 19:30:51 | ||
图片预览




文档简介
(共19张PPT)
数学(北师大版)
九年级 下册
3.6 直线与圆的位置关系
(第二课时)
第三章 圆
课前导入
学习目标
1)理解和掌握切线的性质与判定定理。
2)通过合作探究体会切线的判定和性质的联系。
3)利用切线的性质与判定定理进行计算。
4)掌握三角形内切圆的概念。
重点
理解和掌握切线的性质与判定定理。
难点
利用切线的性质与判定定理进行计算。
探索与思考
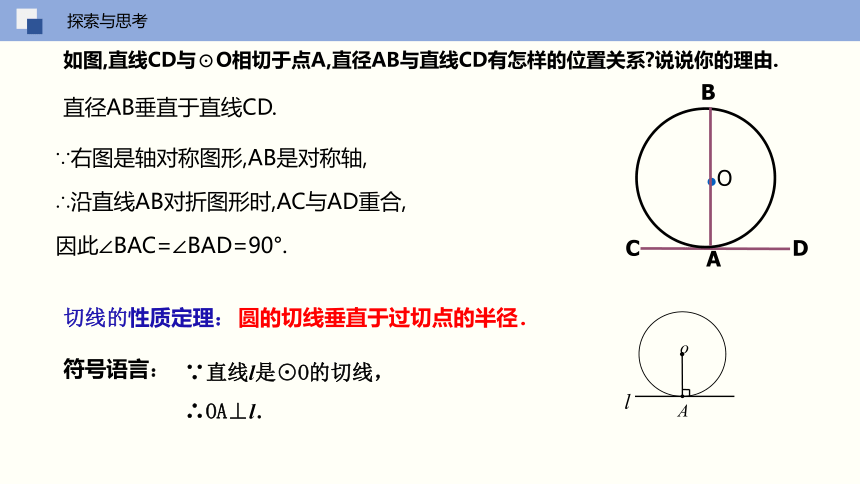
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
直径AB垂直于直线CD.
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,
因此∠BAC=∠BAD=90°.
C
D
B
●O
A
切线的性质定理:
∵直线l是⊙O的切线,
∴OA⊥l.
符号语言:
l
A
o
圆的切线垂直于过切点的半径.
课堂基础练
已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切
A
C
B
┐
解:(1)过点C作CD⊥AB于D.
∵AB=8cm,AC=4cm.
∴∠A=60°.
因此,当半径长为cm时,AB与⊙C相切.
D
┛
课堂基础练
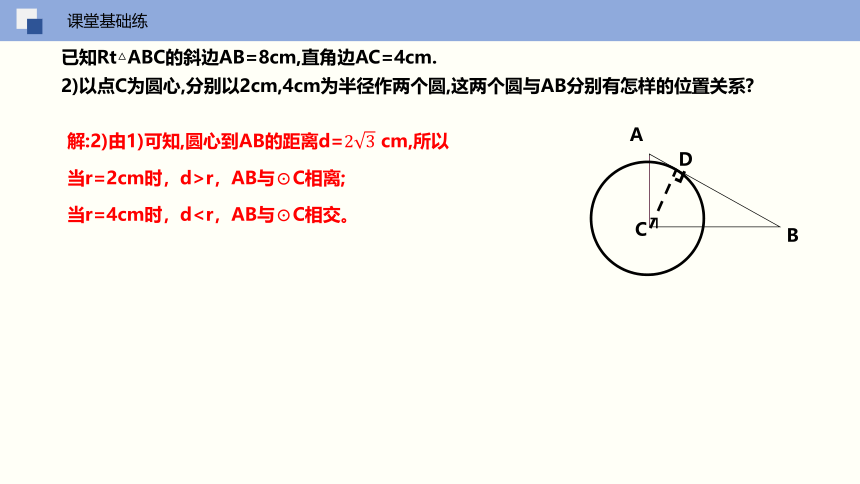
解:2)由1)可知,圆心到AB的距离d= cm,所以
当r=2cm时,d>r,AB与⊙C相离;
当r=4cm时,dA
C
B
┐
D
┛
已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系
探索与思考
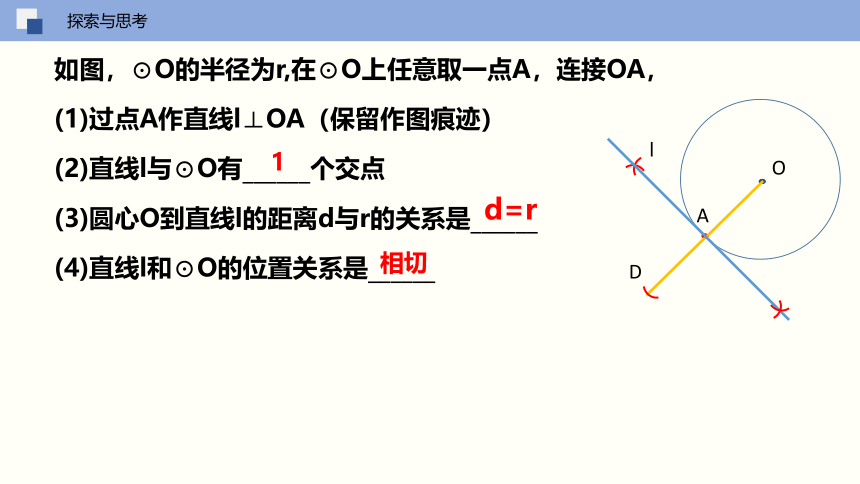
如图,⊙O的半径为r,在⊙O上任意取一点A,连接OA,
(1)过点A作直线l⊥OA(保留作图痕迹)
(2)直线l与⊙O有______个交点
(3)圆心O到直线l的距离d与r的关系是______
(4)直线l和⊙O的位置关系是______
d=r
相切
O
A
D
l
1
探索与思考
l
A
o
切线的判定定理:
∵OA⊥l于点A,OA是半径,
∴直线l是⊙O的切线.
符号语言:
经过半径的外端并且垂直于这条半径的直线是圆的切线。
【提问】要使直线l是圆的切线需要满足哪些条件?
①经过半径的外端;②垂直于这条半径.
课堂基础练
判断下列各直线是不是圆的切线?若不是,请说明原因?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
1)不是,因为没有垂直.
2)不是,因为没有经过半径的外端点A.
课堂基础练
判断下列命题是否正确
⑴ 经过半径外端的直线是圆的切线. ( )
⑵ 垂直于半径的直线是圆的切线. ( )
⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线. ( )
⑷ 和圆只有一个公共点的直线是圆的切线. ( )
⑸ 过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
探索与思考
一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
要使剪得圆的面积最大,这个圆应该与三角形的各边都相切。
探索与思考
一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
A
B
C
0
D
【步骤】
1)分别作∠A, ∠B,∠C的角平分线 。
2)过三条角平分线交点O作BC边垂线,交BC边于点D 。
3)以O为圆心,OD长为半径作圆。
想一想:符合题意这样的圆,可以作出多少个呢?为什么?
三角形内切圆
三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆。
三角形的内心:三角形的内切圆的圆心(即三角形三条角平分线的交点)。
O
⊙O是△ABC的内切圆,
△ABC是⊙O的外切三角形。
A
B
C
课堂小结
圆心的名称
圆心的确定方法
图形
圆心的性质
内心
三角形三边中垂线的交点
三角形三条角平分线的交点
(1)OA=OB=OC
(2)外心不一定在三角形的内部.
(1)到三边的距离相等;
(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
(3)内心一定在三角形内部.
外心
随堂测试
1.平面内,⊙的半径为,点到圆心的距离为,过点可作⊙的切线条数( )
A.条 B.条 C.条 D.无数条
【详解】⊙的半径为,点到圆心的距离为,
,点与⊙的位置关系是:点在⊙的内部,
过点可以作⊙的条切线.故选:A.
2.如图,在△ABC中,∠ACB=90°,AC=6,AB=10.以B为圆心作圆与AC相切,则该圆的半径为( )
A.5 B.4 C.10 D.8
【详解】∵∠ACB=90°,AC=6,AB=10,∴ .
∵∠ACB=90°,∴以B为圆心与AC相切的圆的半径等于线段BC的长,
∴该圆的半径为:8.故选D.
随堂测试
3.如图,A为⊙O外一点,AB与⊙O相切于B点,点P是⊙O上的一个动点,若OB=5,AB=12,则AP的最小值为( )
A.5 B.8 C.13 D.18
【详解】解:连接OA交⊙O于点P,此时AP有最小值,
∵AB为⊙O的切线,∴∠OBA=90°,
∵OB=5,AB=12,∴=13,
∴OP=5,则AP=13﹣5=8,故选:B.
随堂测试
4.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=__________.
【详解】连接OB,
∵BC是⊙O的切线,∴OB⊥BC,
∴∠OBA+∠CBP=90°,
∵OC⊥OA,∴∠A+∠APO=90°,
∵OA=OB,∠OAB=22°,∴∠OAB=∠OBA=22°,
∴∠APO=∠CBP=68°,
∵∠APO=∠CPB,∴∠CPB=∠ABP=68°,
∴∠OCB=180°-68°-68°=44°,
故答案为44°
随堂测试
5.如图,在△ABC中,BC=AC=6,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:DE是⊙O 的切线;
(2)求点O到直线DE的距离.
【详解】(1)证明:连接OD、CD,如图,
∵CD为直径,∴∠BDC=90°,∴CD⊥AB,
∵CB=CA,∴AD=BD,而BO=CO,
∴OD为△CAB的中位线,∴OD∥CA,
∵DE⊥AC,∴OD⊥DE,
∴DE是⊙O的切线;
随堂测试
5.如图,在△ABC中,BC=AC=6,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:DE是⊙O 的切线;
(2)求点O到直线DE的距离.
(2)证明:连接OD,
∵AD=BD,OB=OC,∴DO是△ABC的中位线,
∴DO∥AC,OD=AC=×6=3,又∵DE⊥AC,
∴DE⊥DO,∴点O到直线DE的距离为3.
谢谢~
数学(北师大版)
九年级 下册
3.6 直线与圆的位置关系
(第二课时)
第三章 圆
课前导入
学习目标
1)理解和掌握切线的性质与判定定理。
2)通过合作探究体会切线的判定和性质的联系。
3)利用切线的性质与判定定理进行计算。
4)掌握三角形内切圆的概念。
重点
理解和掌握切线的性质与判定定理。
难点
利用切线的性质与判定定理进行计算。
探索与思考
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
直径AB垂直于直线CD.
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,
因此∠BAC=∠BAD=90°.
C
D
B
●O
A
切线的性质定理:
∵直线l是⊙O的切线,
∴OA⊥l.
符号语言:
l
A
o
圆的切线垂直于过切点的半径.
课堂基础练
已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切
A
C
B
┐
解:(1)过点C作CD⊥AB于D.
∵AB=8cm,AC=4cm.
∴∠A=60°.
因此,当半径长为cm时,AB与⊙C相切.
D
┛
课堂基础练
解:2)由1)可知,圆心到AB的距离d= cm,所以
当r=2cm时,d>r,AB与⊙C相离;
当r=4cm时,d
C
B
┐
D
┛
已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系
探索与思考
如图,⊙O的半径为r,在⊙O上任意取一点A,连接OA,
(1)过点A作直线l⊥OA(保留作图痕迹)
(2)直线l与⊙O有______个交点
(3)圆心O到直线l的距离d与r的关系是______
(4)直线l和⊙O的位置关系是______
d=r
相切
O
A
D
l
1
探索与思考
l
A
o
切线的判定定理:
∵OA⊥l于点A,OA是半径,
∴直线l是⊙O的切线.
符号语言:
经过半径的外端并且垂直于这条半径的直线是圆的切线。
【提问】要使直线l是圆的切线需要满足哪些条件?
①经过半径的外端;②垂直于这条半径.
课堂基础练
判断下列各直线是不是圆的切线?若不是,请说明原因?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
1)不是,因为没有垂直.
2)不是,因为没有经过半径的外端点A.
课堂基础练
判断下列命题是否正确
⑴ 经过半径外端的直线是圆的切线. ( )
⑵ 垂直于半径的直线是圆的切线. ( )
⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线. ( )
⑷ 和圆只有一个公共点的直线是圆的切线. ( )
⑸ 过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
探索与思考
一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
要使剪得圆的面积最大,这个圆应该与三角形的各边都相切。
探索与思考
一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
A
B
C
0
D
【步骤】
1)分别作∠A, ∠B,∠C的角平分线 。
2)过三条角平分线交点O作BC边垂线,交BC边于点D 。
3)以O为圆心,OD长为半径作圆。
想一想:符合题意这样的圆,可以作出多少个呢?为什么?
三角形内切圆
三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆。
三角形的内心:三角形的内切圆的圆心(即三角形三条角平分线的交点)。
O
⊙O是△ABC的内切圆,
△ABC是⊙O的外切三角形。
A
B
C
课堂小结
圆心的名称
圆心的确定方法
图形
圆心的性质
内心
三角形三边中垂线的交点
三角形三条角平分线的交点
(1)OA=OB=OC
(2)外心不一定在三角形的内部.
(1)到三边的距离相等;
(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;
(3)内心一定在三角形内部.
外心
随堂测试
1.平面内,⊙的半径为,点到圆心的距离为,过点可作⊙的切线条数( )
A.条 B.条 C.条 D.无数条
【详解】⊙的半径为,点到圆心的距离为,
,点与⊙的位置关系是:点在⊙的内部,
过点可以作⊙的条切线.故选:A.
2.如图,在△ABC中,∠ACB=90°,AC=6,AB=10.以B为圆心作圆与AC相切,则该圆的半径为( )
A.5 B.4 C.10 D.8
【详解】∵∠ACB=90°,AC=6,AB=10,∴ .
∵∠ACB=90°,∴以B为圆心与AC相切的圆的半径等于线段BC的长,
∴该圆的半径为:8.故选D.
随堂测试
3.如图,A为⊙O外一点,AB与⊙O相切于B点,点P是⊙O上的一个动点,若OB=5,AB=12,则AP的最小值为( )
A.5 B.8 C.13 D.18
【详解】解:连接OA交⊙O于点P,此时AP有最小值,
∵AB为⊙O的切线,∴∠OBA=90°,
∵OB=5,AB=12,∴=13,
∴OP=5,则AP=13﹣5=8,故选:B.
随堂测试
4.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=__________.
【详解】连接OB,
∵BC是⊙O的切线,∴OB⊥BC,
∴∠OBA+∠CBP=90°,
∵OC⊥OA,∴∠A+∠APO=90°,
∵OA=OB,∠OAB=22°,∴∠OAB=∠OBA=22°,
∴∠APO=∠CBP=68°,
∵∠APO=∠CPB,∴∠CPB=∠ABP=68°,
∴∠OCB=180°-68°-68°=44°,
故答案为44°
随堂测试
5.如图,在△ABC中,BC=AC=6,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:DE是⊙O 的切线;
(2)求点O到直线DE的距离.
【详解】(1)证明:连接OD、CD,如图,
∵CD为直径,∴∠BDC=90°,∴CD⊥AB,
∵CB=CA,∴AD=BD,而BO=CO,
∴OD为△CAB的中位线,∴OD∥CA,
∵DE⊥AC,∴OD⊥DE,
∴DE是⊙O的切线;
随堂测试
5.如图,在△ABC中,BC=AC=6,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:DE是⊙O 的切线;
(2)求点O到直线DE的距离.
(2)证明:连接OD,
∵AD=BD,OB=OC,∴DO是△ABC的中位线,
∴DO∥AC,OD=AC=×6=3,又∵DE⊥AC,
∴DE⊥DO,∴点O到直线DE的距离为3.
谢谢~
