15.2.1 分式的乘除(1)课件(共25张PPT)
文档属性
| 名称 | 15.2.1 分式的乘除(1)课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 957.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 20:24:11 | ||
图片预览







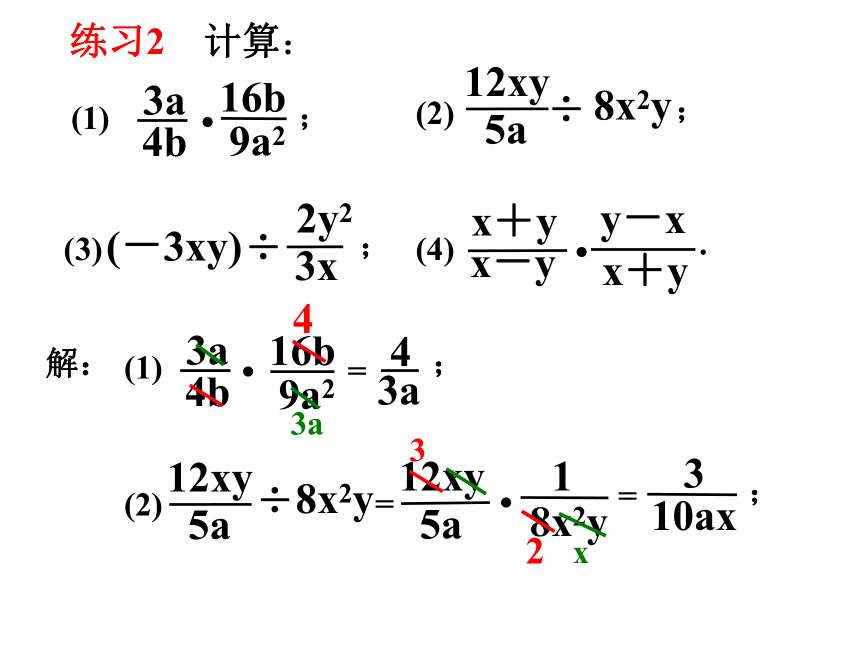
文档简介
(共25张PPT)
人教版 八年级上册
15. 2. 1分式的乘除(1)
教学目标:
1.理解分式的乘除法法则,体会类比的思想.
2.会根据分式的乘除法法则进行简单的运算,
并理解其算理.
教学重点:分式的乘除法法则的运用.
课件说明
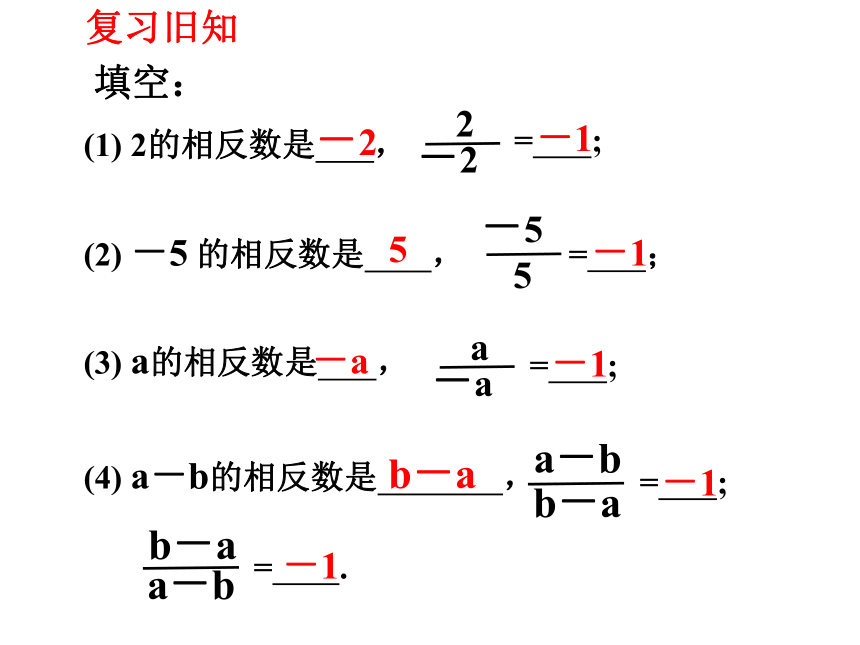
(1) 2的相反数是 ,
(2) -5 的相反数是 ,
2
-2
= ;
5
-5
= ;
(3) a的相反数是 ,
a
-a
= ;
(4) a-b的相反数是 ,
a-b
b-a
= ;
a-b
b-a
= .
5
-2
-a
b-a
-1
-1
-1
-1
-1
填空:
复习旧知
在计算的过程中,你运用了分数的什么法则?你能
叙述这个法则吗?
计算:
(1)
3
5
13
2
(2)
3
5
÷
13
2
×
=
39
10
=
3
5
×
2
13
=
6
65
分数乘分数,用分子的积作为积的分子,分母的积作为积的分母. :
分数除以分数,把除式的分子、分母颠倒位置后,与被除式相乘.
如果将分数换成分式,那么你能类比分数的乘除法法则,说出分式的乘除法法则吗?
怎样用字母来表示分式的乘除法法则呢?
(1)
3
5
13
2
(2)
3
5
÷
13
2
×
=
39
10
=
3
5
×
2
13
=
6
65
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母. :
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
如何用文字语言来描述?
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
分式的乘除法法则:
分式乘法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
分式除法法则:
a
b
c
d
=
a c
b d
;
a
b
c
d
a
b
d
c
=
=
a d
b c
.
÷
学习新知
-5a2b2
4cd
(2)
ab3
2c2
例1 计算:
解:
(1)
4x
3y
y
2x3
(1)
4x
3y
y
2x3
;
=
3x2
2
;
÷
-5a2b2
4cd
=
=
-
2bd
5ac
.
2c2
ab3
(2)
÷
.
ab3
2c2
-5a2b2
4cd
2
x2
1
2
c
a
b
例题解析
2a
b
练习1 计算:
(1)
(2)
(3)
解:
(1)
=
÷
(2)
÷
=
=
(3)
=
-
;
;
.
b
a
a
c
b
c
2
a
b
2a
2
a
4
b
ny
mx
-my
nx
y2
x2
b
a
a
c
2
a
b
2a
ny
mx
-my
nx
-1
练习2 计算:
(1)
(2)
÷
8x2y
(3)
(-3xy)
÷
(4)
解:
(1)
3a
4b
16b
9a2
;
;
=
4
3a
(2)
12xy
5a
÷
8x2y
=
8x2y
1
=
3
10ax
;
;
;
.
12xy
5a
3a
4b
16b
9a2
12xy
5a
2y2
3x
x+y
x-y
y-x
x+y
4
3a
2
3
x
练习2 计算:
(1)
3a
4b
16b
9a2
(2)
12xy
5a
÷
8x2y
(3)
(-3xy)
÷
(4)
解:
(3)
;
;
1
(4)
=
;
;
.
-
.
2y2
3x
(-3xy)
÷
(-3xy)
3x
2y2
=
=
-
9x2
2y
x+y
x-y
y-x
x+y
(x-y) 与(y-x)互为相反数
-1
x+y
x-y
y-x
x+y
2y2
3x
y
分子或分母是多项式的两个分式如何乘除呢?
例2 计算:
(1)
a2-4a+4
a2-2a+1
a-1
a2-4
(2)
1
49-m2
÷
1
m2-7m
;
.
解:
(1)
a2-4a+4
a2-2a+1
a-1
a2-4
=
(a-2)2
(a-1)2
=
(a-2)
(a-1)
(a+2)
(a-1)
(a+2)
a-2
(a-1)
(a-2)
分子或分母是多项式的两个分式如何乘除呢?
例2 计算:
(1)
a2-4a+4
a2-2a+1
a-1
a2-4
(2)
1
49-m2
÷
1
m2-7m
;
.
解:
(2)
=
=
1
49-m2
÷
1
m2-7m
m(m-7)
1
-
(7-m)
1
(7+m)
7+m
m
-1
(7-m) 与(m-7)互为相反数
分子或分母中含有多项式的两个分式相乘,需要先将多项式因式分解,然后利用分式的基本性质进行约分,再利用分式的乘除法法则进行运算.
(2)
=
=
1
49-m2
÷
1
m2-7m
1
(7+m)(7-m)
m(m-7)
1
m
m+7
-
(1)
a2-4a+4
a2-2a+1
a-1
a2-4
=
(a-2)2
(a-1) 2
a-1
(a+2)(a-2)
a-2
(a+2)(a-1)
=
x-2
x+3
x2-9
x2-4
(3)
(2)
4y2-x2
x2+2xy+y2
÷
x-2y
2x2+2xy
3a-3b
10ab
25a2b3
a2-b2
(1)
练习3 计算:
2(a+b)
(a+b)
3a-3b
10ab
=
25a2b3
a2-b2
3(a-b)
10ab
(1)
25a2b3
(a-b)
=
15ab2
2
5
ab2
解:
(2)
4y2-x2
x2+2xy+y2
÷
x-2y
2x2+2xy
=
(2y+x)(2y-x)
(x+y)2
x-2y
2x(x+y)
=
-
x+y
2x(2y+x)
=
-
x+y
4xy+2x2
(x+y)
-1
(x-2)
(x+3)(x-3)
x-2
x+3
x2-9
x2-4
=
x-2
x+3
(x+2)
=
x-3
x+2
(3)
(1)本节课学习了哪些主要内容?
(2)分式的乘除法运算与分数的乘除法运算
有什么区别和联系?
课堂小结
1.计算
5c2
6ab
的结果是( ).
●
3b
10c
B. C. D.
c2
4a
c
4a
4a
c
1
巩固新知
C
2.化简
m
m-1
的结果是( ).
÷
m2
m-1
B. C. D.
m-1
1
m-1
m
m
1
B
3.化简
1
a2-a
的结果是( ).
a
a-1
B. C. D.
a2
1
1
a
1
a-1
a3-a2
A
4.当x=2023,y=1953时,代数式
的值为 ( ).
A.70 B.-70 C.3976 D.-3976
x4-y4
x2-2xy+y2
y-x
x2+y2
。
;
=
x+2
x-1
6.化简:
x-1
x-2
÷
x2-4
x2-2x+1
=
.
5.计算:
xy+y2
5xy2
15x2y
x2-y2
(1)
(2)
a
a+1
÷
(a2+a)=
.
.
3x
x-y
1
a2
7.化简: ,然后选择一
个使分式有意义的数代入求值.
x2+2x+1
x+2
·
x2-1
x-1
解:
x2+2x+1
x+2
·
x2-1
x-1
(x+1)(x-1)
=
(x+1)2
x+2
x-1
=
x+1
x+2
当x=2时,
原式=
2+1
2+2
=
3
4
今天作业
课本P146页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
15. 2. 1分式的乘除(1)
教学目标:
1.理解分式的乘除法法则,体会类比的思想.
2.会根据分式的乘除法法则进行简单的运算,
并理解其算理.
教学重点:分式的乘除法法则的运用.
课件说明
(1) 2的相反数是 ,
(2) -5 的相反数是 ,
2
-2
= ;
5
-5
= ;
(3) a的相反数是 ,
a
-a
= ;
(4) a-b的相反数是 ,
a-b
b-a
= ;
a-b
b-a
= .
5
-2
-a
b-a
-1
-1
-1
-1
-1
填空:
复习旧知
在计算的过程中,你运用了分数的什么法则?你能
叙述这个法则吗?
计算:
(1)
3
5
13
2
(2)
3
5
÷
13
2
×
=
39
10
=
3
5
×
2
13
=
6
65
分数乘分数,用分子的积作为积的分子,分母的积作为积的分母. :
分数除以分数,把除式的分子、分母颠倒位置后,与被除式相乘.
如果将分数换成分式,那么你能类比分数的乘除法法则,说出分式的乘除法法则吗?
怎样用字母来表示分式的乘除法法则呢?
(1)
3
5
13
2
(2)
3
5
÷
13
2
×
=
39
10
=
3
5
×
2
13
=
6
65
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母. :
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
如何用文字语言来描述?
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
分式的乘除法法则:
分式乘法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
分式除法法则:
a
b
c
d
=
a c
b d
;
a
b
c
d
a
b
d
c
=
=
a d
b c
.
÷
学习新知
-5a2b2
4cd
(2)
ab3
2c2
例1 计算:
解:
(1)
4x
3y
y
2x3
(1)
4x
3y
y
2x3
;
=
3x2
2
;
÷
-5a2b2
4cd
=
=
-
2bd
5ac
.
2c2
ab3
(2)
÷
.
ab3
2c2
-5a2b2
4cd
2
x2
1
2
c
a
b
例题解析
2a
b
练习1 计算:
(1)
(2)
(3)
解:
(1)
=
÷
(2)
÷
=
=
(3)
=
-
;
;
.
b
a
a
c
b
c
2
a
b
2a
2
a
4
b
ny
mx
-my
nx
y2
x2
b
a
a
c
2
a
b
2a
ny
mx
-my
nx
-1
练习2 计算:
(1)
(2)
÷
8x2y
(3)
(-3xy)
÷
(4)
解:
(1)
3a
4b
16b
9a2
;
;
=
4
3a
(2)
12xy
5a
÷
8x2y
=
8x2y
1
=
3
10ax
;
;
;
.
12xy
5a
3a
4b
16b
9a2
12xy
5a
2y2
3x
x+y
x-y
y-x
x+y
4
3a
2
3
x
练习2 计算:
(1)
3a
4b
16b
9a2
(2)
12xy
5a
÷
8x2y
(3)
(-3xy)
÷
(4)
解:
(3)
;
;
1
(4)
=
;
;
.
-
.
2y2
3x
(-3xy)
÷
(-3xy)
3x
2y2
=
=
-
9x2
2y
x+y
x-y
y-x
x+y
(x-y) 与(y-x)互为相反数
-1
x+y
x-y
y-x
x+y
2y2
3x
y
分子或分母是多项式的两个分式如何乘除呢?
例2 计算:
(1)
a2-4a+4
a2-2a+1
a-1
a2-4
(2)
1
49-m2
÷
1
m2-7m
;
.
解:
(1)
a2-4a+4
a2-2a+1
a-1
a2-4
=
(a-2)2
(a-1)2
=
(a-2)
(a-1)
(a+2)
(a-1)
(a+2)
a-2
(a-1)
(a-2)
分子或分母是多项式的两个分式如何乘除呢?
例2 计算:
(1)
a2-4a+4
a2-2a+1
a-1
a2-4
(2)
1
49-m2
÷
1
m2-7m
;
.
解:
(2)
=
=
1
49-m2
÷
1
m2-7m
m(m-7)
1
-
(7-m)
1
(7+m)
7+m
m
-1
(7-m) 与(m-7)互为相反数
分子或分母中含有多项式的两个分式相乘,需要先将多项式因式分解,然后利用分式的基本性质进行约分,再利用分式的乘除法法则进行运算.
(2)
=
=
1
49-m2
÷
1
m2-7m
1
(7+m)(7-m)
m(m-7)
1
m
m+7
-
(1)
a2-4a+4
a2-2a+1
a-1
a2-4
=
(a-2)2
(a-1) 2
a-1
(a+2)(a-2)
a-2
(a+2)(a-1)
=
x-2
x+3
x2-9
x2-4
(3)
(2)
4y2-x2
x2+2xy+y2
÷
x-2y
2x2+2xy
3a-3b
10ab
25a2b3
a2-b2
(1)
练习3 计算:
2(a+b)
(a+b)
3a-3b
10ab
=
25a2b3
a2-b2
3(a-b)
10ab
(1)
25a2b3
(a-b)
=
15ab2
2
5
ab2
解:
(2)
4y2-x2
x2+2xy+y2
÷
x-2y
2x2+2xy
=
(2y+x)(2y-x)
(x+y)2
x-2y
2x(x+y)
=
-
x+y
2x(2y+x)
=
-
x+y
4xy+2x2
(x+y)
-1
(x-2)
(x+3)(x-3)
x-2
x+3
x2-9
x2-4
=
x-2
x+3
(x+2)
=
x-3
x+2
(3)
(1)本节课学习了哪些主要内容?
(2)分式的乘除法运算与分数的乘除法运算
有什么区别和联系?
课堂小结
1.计算
5c2
6ab
的结果是( ).
●
3b
10c
B. C. D.
c2
4a
c
4a
4a
c
1
巩固新知
C
2.化简
m
m-1
的结果是( ).
÷
m2
m-1
B. C. D.
m-1
1
m-1
m
m
1
B
3.化简
1
a2-a
的结果是( ).
a
a-1
B. C. D.
a2
1
1
a
1
a-1
a3-a2
A
4.当x=2023,y=1953时,代数式
的值为 ( ).
A.70 B.-70 C.3976 D.-3976
x4-y4
x2-2xy+y2
y-x
x2+y2
。
;
=
x+2
x-1
6.化简:
x-1
x-2
÷
x2-4
x2-2x+1
=
.
5.计算:
xy+y2
5xy2
15x2y
x2-y2
(1)
(2)
a
a+1
÷
(a2+a)=
.
.
3x
x-y
1
a2
7.化简: ,然后选择一
个使分式有意义的数代入求值.
x2+2x+1
x+2
·
x2-1
x-1
解:
x2+2x+1
x+2
·
x2-1
x-1
(x+1)(x-1)
=
(x+1)2
x+2
x-1
=
x+1
x+2
当x=2时,
原式=
2+1
2+2
=
3
4
今天作业
课本P146页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
