2.1 认识一元二次方程 课件(共17张PPT)
文档属性
| 名称 | 2.1 认识一元二次方程 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 206.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-23 10:03:47 | ||
图片预览






文档简介
(共17张PPT)
2.1 认识一元二次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 经历由具体问题抽象出一元二次方程的概念的过程,进一步体会方程是刻画现实世界中数量关系的一个有效数学模型.
2. 理解一元二次方程及其相关概念.
3. 经历估计一元二次方程解的过程,增进对方程解的认识,进一步培养估算意识和能力,发展数感.
学习目标
重点
难点
重点
问题一 幼儿园某教室矩形地面的长为 8m,宽为 5m,现准备在地面正中间铺设一块面积为 18m2 的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出这个宽度吗?
新课引入
5m
8m
如果设所求的宽度为 x m,那么你能列出怎样方程?
分析:如果设所求的宽为 x m,那么地毯中央长方形图案的长为 m,宽为 m.
(8 - 2x)
(5 - 2x)
(8 - 2x)(5 - 2x ) = 18
问题二 观察下面等式:
102+ 112+ 122 = 132 + 142.
你还能找到五个连续整数,使前三个数的平方和等于后两个数的平方和吗
如果将这五个连续整数中的第一个数设为 x. 那么怎样用含 x 的代数式表示其余四个数?根据题意,你能列出怎样的方程?
分析:如果设五个连续整数中的第一个数为 x,那么后面四个数依次可表示为: , , , .
x+1
x+2
x+3
x+4
x + ( x + 1)2 + ( x + 2 )2 = ( x + 3)2 + ( x + 4 )2
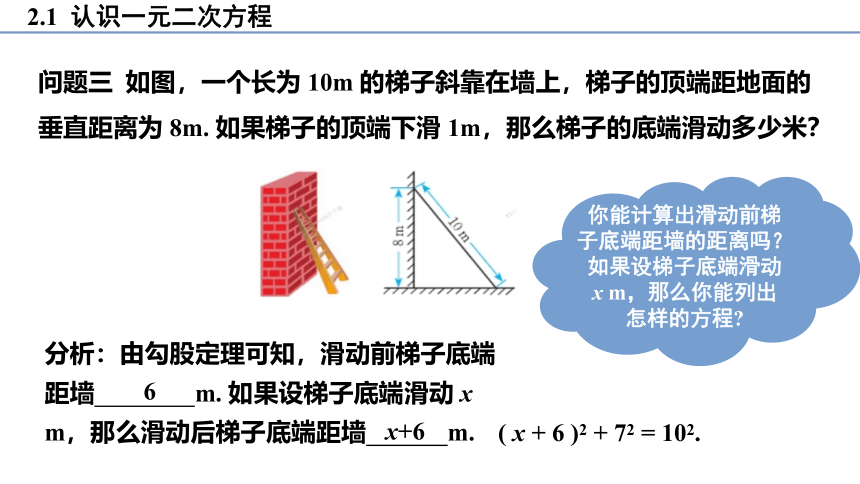
问题三 如图,一个长为 10m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8m. 如果梯子的顶端下滑 1m,那么梯子的底端滑动多少米?
你能计算出滑动前梯子底端距墙的距离吗?如果设梯子底端滑动 x m,那么你能列出怎样的方程
分析:由勾股定理可知,滑动前梯子底端距墙 m. 如果设梯子底端滑动 x m,那么滑动后梯子底端距墙 m.
6
x+6
( x + 6 )2 + 72 = 102.
由上面三个问题,我们可以得到三个方程:
新知学习
(8 - 2x)(5 - 2x ) = 18,
x + ( x + 1)2 + ( x + 2 )2 = ( x + 3)2 + ( x + 4 )2,
( x + 6 )2 + 72 = 102.
这三个方程有什么共同特点?
上面的方程都是只含有一个未知数 x 的整式方程,并且都可以化成
ax2 + bx + c = 0 ( a,b,c 为常数,a ≠ 0 ) 的形式,这样的方程叫做一元二次方程 ( quadratic equation with one unknown ).
我们把 ax2 + bx + c = 0 (a,b,c为常数,a ≠ 0 ) 称为一元二次方程的一般形式,其中 ax2,bx,c分别称为二次项、一次项和常数项, a,b分别称为二次项系数和一次项系数.
针对训练
1. 根据题意列出一元二次方程:已知直角三角形的三边长为连续整数,求它的三边长.
2.把方程( 3x + 2 )2 = 4 ( x - 3 )2 化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
x2 + (x + 1)2 = (x + 2)2
解:9x2 + 12x + 4 = 4( x2 - 6x + 9)
9x2 + 12x + 4 = 4x2 - 24x + 36
5x2 + 36x - 32 = 0
二次项系数:5
一次项系数:36
常数项:-32
还有其他方法吗?
你能设法估计问题一中四周未铺地毯部分的宽度 x (m) 吗?
我们知道,x 满足方程 ( 8 - 2x )( 5 - 2x ) = 18.
(1) x 可能小于 0 吗?可能大于 4 吗?可能大于 2.5 吗?说说你的理由.
(2) 你能确定 x 的大致范围吗?
思考
x 小于 0 时,( 8 - 2x ) > 8,( 5 - 2x ) > 5,( 8 - 2x )( 5 - 2x ) > 40. 故不可能.
x 大于 4 时,( 8 - 2x )小于0,不符合实际,
x 大于 2.5 时, ( 5 - 2x ) 小于0,不符合实际.
0 < x < 2.5.
(3) 填写下表:
(4) 你知道所求宽度 x (m)是多少吗?还有其他求解方法吗?与同伴交流.
x 0.5 1 1.5 2.5
(8 - 2x)(5 - 2x)
28
18
10
0
x = 1
问题三中,梯子底端滑动的距离 x (m) 满足方程 ( x + 6 )2 + 72 = 102,也就是 x2 + 12x - 15 = 0.
(1) 小明认为底端也滑动了 1m,他的说法正确吗?为什么?
(2) 底端滑动的距离可能是 2m 吗?可能是 3m 吗?为什么?
不正确,1 + 12 - 15 = -2.
距离是 2m 不可能,4 + 24 - 15 = 13.
距离是 3m 不满足方程,不是方程的解
小亮把他的求解过程整理如下:
x 0 0.5 1 1.5 2
x2 + 12 x - 15 -15 -8.75 -2 5.25 13
所以 1 < x <1.5,
进一步计算:
x 1.1 1.2 1.3 1.4
x2 + 12 x - 15 -0.59 0.84 2.29 3.76
所以 1.1 < x <1.2 .
针对训练
五个连续整数,前三个数的平方和等于后面两个数的平方和. 你能求出五个整数分别是多少吗?
解:设第一个数为 x,则可列出方程
x2 + (x+1)2 + (x+2)2 = (x+3)2 + (x+4)2.
化简可得 x2 + x2 + 2x + 1 + x2 + 4x + 4 = x2 + 6x + 9 + x2 + 8x + 16,
即 x2 - 8x - 20 = 0.
列表:
x -4 -2 0 2 4 6 8 10 12
x2 - 8x - 20 28 0 -20 -32 -36 -32 -20 0 28
解出 x = -2 或 10,这五个数分别是 -2, -1, 0, 1, 2 或者 10, 11, 12, 13, 14 .
课堂小结
一元二次方程
概念
是整式方程;
只含一个未知数;
最高次数是2.
一般形式
ax2 + bx + c = 0 (a ≠ 0)
解一元二次方程
(“两边夹”方法)
确定其解的大致范围
列表、计算
进行两边“夹逼”
……
求得近似解
估计一元二次方程的解,应先确定方程解的大致范围,然后在这一范围内有规律地取一些未知数的值,如果把一个值代入方程使得左边的计算结果小于右边的计算结果,把另一个值代入方程使得左边的计算结果大于右边的计算结果,那么方程的解就在这两个值之间.
2.1 认识一元二次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 经历由具体问题抽象出一元二次方程的概念的过程,进一步体会方程是刻画现实世界中数量关系的一个有效数学模型.
2. 理解一元二次方程及其相关概念.
3. 经历估计一元二次方程解的过程,增进对方程解的认识,进一步培养估算意识和能力,发展数感.
学习目标
重点
难点
重点
问题一 幼儿园某教室矩形地面的长为 8m,宽为 5m,现准备在地面正中间铺设一块面积为 18m2 的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出这个宽度吗?
新课引入
5m
8m
如果设所求的宽度为 x m,那么你能列出怎样方程?
分析:如果设所求的宽为 x m,那么地毯中央长方形图案的长为 m,宽为 m.
(8 - 2x)
(5 - 2x)
(8 - 2x)(5 - 2x ) = 18
问题二 观察下面等式:
102+ 112+ 122 = 132 + 142.
你还能找到五个连续整数,使前三个数的平方和等于后两个数的平方和吗
如果将这五个连续整数中的第一个数设为 x. 那么怎样用含 x 的代数式表示其余四个数?根据题意,你能列出怎样的方程?
分析:如果设五个连续整数中的第一个数为 x,那么后面四个数依次可表示为: , , , .
x+1
x+2
x+3
x+4
x + ( x + 1)2 + ( x + 2 )2 = ( x + 3)2 + ( x + 4 )2
问题三 如图,一个长为 10m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8m. 如果梯子的顶端下滑 1m,那么梯子的底端滑动多少米?
你能计算出滑动前梯子底端距墙的距离吗?如果设梯子底端滑动 x m,那么你能列出怎样的方程
分析:由勾股定理可知,滑动前梯子底端距墙 m. 如果设梯子底端滑动 x m,那么滑动后梯子底端距墙 m.
6
x+6
( x + 6 )2 + 72 = 102.
由上面三个问题,我们可以得到三个方程:
新知学习
(8 - 2x)(5 - 2x ) = 18,
x + ( x + 1)2 + ( x + 2 )2 = ( x + 3)2 + ( x + 4 )2,
( x + 6 )2 + 72 = 102.
这三个方程有什么共同特点?
上面的方程都是只含有一个未知数 x 的整式方程,并且都可以化成
ax2 + bx + c = 0 ( a,b,c 为常数,a ≠ 0 ) 的形式,这样的方程叫做一元二次方程 ( quadratic equation with one unknown ).
我们把 ax2 + bx + c = 0 (a,b,c为常数,a ≠ 0 ) 称为一元二次方程的一般形式,其中 ax2,bx,c分别称为二次项、一次项和常数项, a,b分别称为二次项系数和一次项系数.
针对训练
1. 根据题意列出一元二次方程:已知直角三角形的三边长为连续整数,求它的三边长.
2.把方程( 3x + 2 )2 = 4 ( x - 3 )2 化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
x2 + (x + 1)2 = (x + 2)2
解:9x2 + 12x + 4 = 4( x2 - 6x + 9)
9x2 + 12x + 4 = 4x2 - 24x + 36
5x2 + 36x - 32 = 0
二次项系数:5
一次项系数:36
常数项:-32
还有其他方法吗?
你能设法估计问题一中四周未铺地毯部分的宽度 x (m) 吗?
我们知道,x 满足方程 ( 8 - 2x )( 5 - 2x ) = 18.
(1) x 可能小于 0 吗?可能大于 4 吗?可能大于 2.5 吗?说说你的理由.
(2) 你能确定 x 的大致范围吗?
思考
x 小于 0 时,( 8 - 2x ) > 8,( 5 - 2x ) > 5,( 8 - 2x )( 5 - 2x ) > 40. 故不可能.
x 大于 4 时,( 8 - 2x )小于0,不符合实际,
x 大于 2.5 时, ( 5 - 2x ) 小于0,不符合实际.
0 < x < 2.5.
(3) 填写下表:
(4) 你知道所求宽度 x (m)是多少吗?还有其他求解方法吗?与同伴交流.
x 0.5 1 1.5 2.5
(8 - 2x)(5 - 2x)
28
18
10
0
x = 1
问题三中,梯子底端滑动的距离 x (m) 满足方程 ( x + 6 )2 + 72 = 102,也就是 x2 + 12x - 15 = 0.
(1) 小明认为底端也滑动了 1m,他的说法正确吗?为什么?
(2) 底端滑动的距离可能是 2m 吗?可能是 3m 吗?为什么?
不正确,1 + 12 - 15 = -2.
距离是 2m 不可能,4 + 24 - 15 = 13.
距离是 3m 不满足方程,不是方程的解
小亮把他的求解过程整理如下:
x 0 0.5 1 1.5 2
x2 + 12 x - 15 -15 -8.75 -2 5.25 13
所以 1 < x <1.5,
进一步计算:
x 1.1 1.2 1.3 1.4
x2 + 12 x - 15 -0.59 0.84 2.29 3.76
所以 1.1 < x <1.2 .
针对训练
五个连续整数,前三个数的平方和等于后面两个数的平方和. 你能求出五个整数分别是多少吗?
解:设第一个数为 x,则可列出方程
x2 + (x+1)2 + (x+2)2 = (x+3)2 + (x+4)2.
化简可得 x2 + x2 + 2x + 1 + x2 + 4x + 4 = x2 + 6x + 9 + x2 + 8x + 16,
即 x2 - 8x - 20 = 0.
列表:
x -4 -2 0 2 4 6 8 10 12
x2 - 8x - 20 28 0 -20 -32 -36 -32 -20 0 28
解出 x = -2 或 10,这五个数分别是 -2, -1, 0, 1, 2 或者 10, 11, 12, 13, 14 .
课堂小结
一元二次方程
概念
是整式方程;
只含一个未知数;
最高次数是2.
一般形式
ax2 + bx + c = 0 (a ≠ 0)
解一元二次方程
(“两边夹”方法)
确定其解的大致范围
列表、计算
进行两边“夹逼”
……
求得近似解
估计一元二次方程的解,应先确定方程解的大致范围,然后在这一范围内有规律地取一些未知数的值,如果把一个值代入方程使得左边的计算结果小于右边的计算结果,把另一个值代入方程使得左边的计算结果大于右边的计算结果,那么方程的解就在这两个值之间.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
