2.3.2 用公式法求解一元二次方程在实际生活中的应用 课件(共19张PPT)
文档属性
| 名称 | 2.3.2 用公式法求解一元二次方程在实际生活中的应用 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 165.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 11:05:57 | ||
图片预览




文档简介
(共19张PPT)
2.3.2 用公式法求解一元二次方程在实际生活中的应用
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 掌握面积法建立一元二次方程的数学模型.
2. 能运用一元二次方程解决与面积有关的实际问题.
学习目标
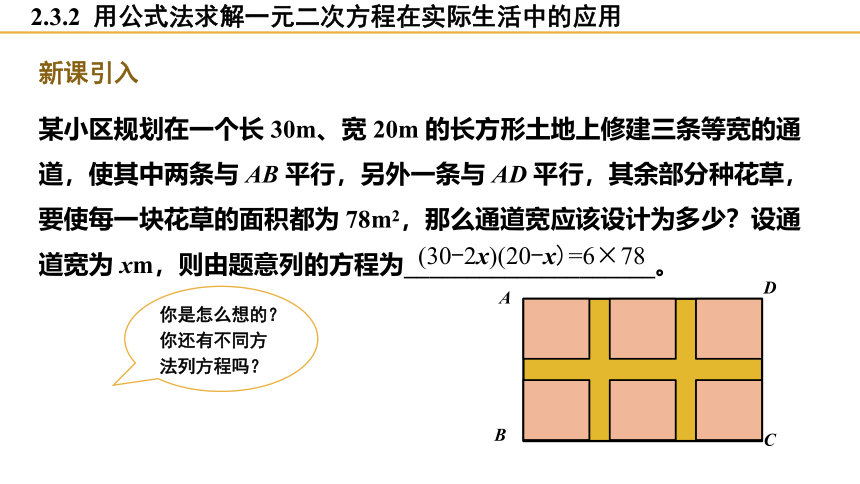
某小区规划在一个长 30m、宽 20m 的长方形土地上修建三条等宽的通道,使其中两条与 AB 平行,另外一条与 AD 平行,其余部分种花草,要使每一块花草的面积都为 78m2,那么通道宽应该设计为多少?设通道宽为 xm,则由题意列的方程为____________________。
新课引入
(30-2x)(20-x)=6×78
C
B
D
A
你是怎么想的?
你还有不同方法列方程吗?
某小区规划在一个长 30m、宽 20m 的长方形土地上修建三条等宽的通道,使其中两条与 AB 平行,另外一条与 AD 平行,其余部分种花草,要使每一块花草的面积都为 78m2,那么通道宽应该设计为多少?设通道宽为 x m,则由题意列的方程为____________________。
我列的方程是
30x+20×2x-2x2=30×20-6×78
你能解释这个方程吗?
C
B
D
A
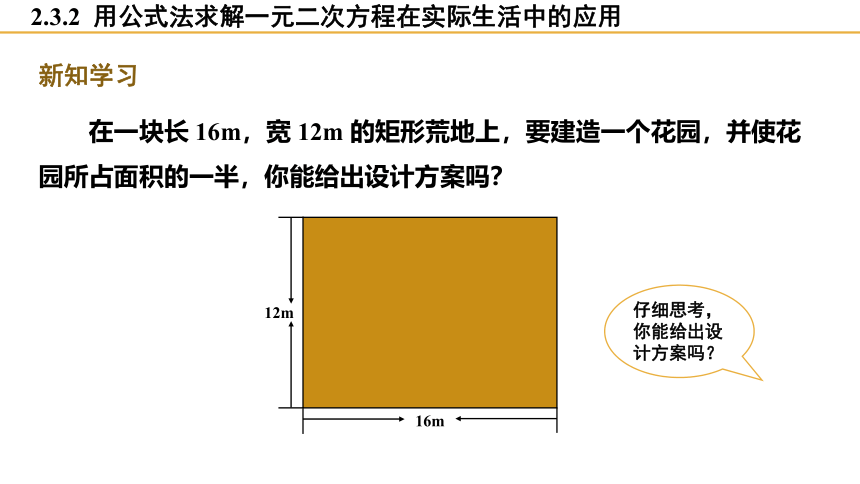
在一块长 16m,宽 12m 的矩形荒地上,要建造一个花园,并使花园所占面积的一半,你能给出设计方案吗?
新知学习
12m
16m
仔细思考,你能给出设计方案吗?
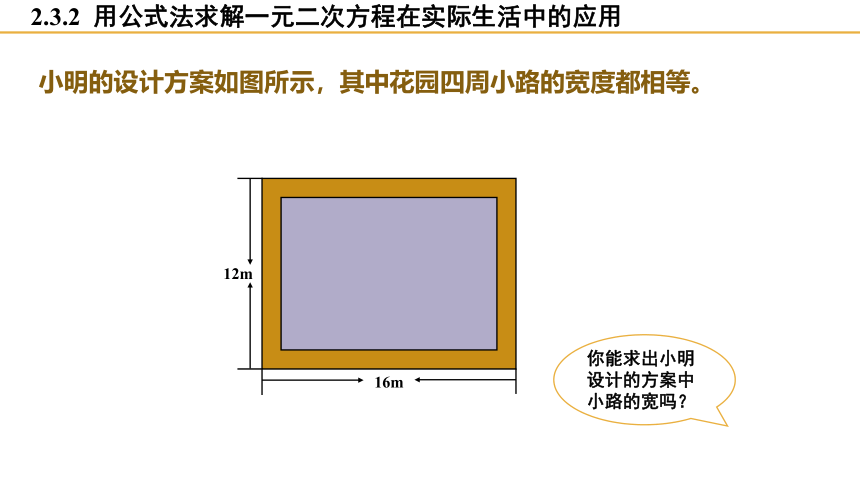
小明的设计方案如图所示,其中花园四周小路的宽度都相等。
12m
16m
你能求出小明设计的方案中小路的宽吗?
12m
16m
解:设小路宽为 x m,则有
( 16 - 2x )( 12 - 2x ) = 12 × 16 ÷ 2,
整理,得 x2 - 14x + 24 = 0,
解得 x1 = 2,x2 = 12 .
小明说他的答案是 2m 或 12m,他的答案对吗?
当 x2 =12 时,小路宽和矩形荒地宽相等,不符合题意,故舍去.
答: 如图,设计小路宽为 2 m
小亮的设计方案如图所示,其中花园每个角上的扇形都相等。
12m
16m
xm
你能帮小亮求出图中的 x 吗?
12m
16m
xm
解:设扇形的半径为 x m,则有
πx2 = 12×16÷2,
解得 x1= ,x2= - < 0 ( 舍去 ).
答: 如图,设计小路宽为 m.
温馨提示
在小明的结果中,小路的宽 12m,符合方程的解,但是荒地的宽为 12m,小路的宽不可能为 12m,因而它不是实际问题的解,应舍去,而小路的宽 2m 符合这个实际问题,所以小路的宽是 2m .
同理,在小亮的结果中 不是实际问题的解,所以圆的半径为 ≈ 5.5m .
用“求根公式法”解一元二次方程时,所得的解不一定符合实际,因此,应用一元二次方程解决实际问题要“检验”.
你还有其他设计方案吗?与小伙伴交流.
针对训练
1. 对于花园设计问题,小颖的设计方案如图所示,你能帮她求出图中 x吗?
12m
16m
x m
x m
解:设小路宽为 x m,则有
( 16 - x )( 12 - x ) = 12 × 16 ÷ 2,
整理,得 x2 - 28x + 96 = 0,
解得 x1 = 4,x2 = 24 ( 不合题意,舍去 ) .
答:小路宽为4 m
12m
16m
x m
x m
2. 在一幅长 90 cm、宽 40 cm 的风景画的四周外围镶上一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂画面积的 72%,那么金色纸边的宽度应该是多少?
解:设金边的宽为 x cm,则有
( 90 + 2x )( 40 + 2x ) × 72% = 90 × 40,
整理,得 x2 + 65x - 350 = 0,
解得 x1 = 5,x2 = -70 ( 不合题意,舍去 ) .
则金色纸边的宽度应该是 5cm.
3. 某农场要建一个长方形的养鸡场,鸡场的一边靠墙 ( 墙长 25 m ),另三边用木栏围成,木栏长 40m.
(1) 鸡场的面积能达到 180 m2 吗?能达到 200 m2 吗?
解:设与墙垂直的一边长 xm,则与墙平行的一边长( 40 - 2x )m.
则有 x( 40 - 2x ) = 180,
整理,得 -2x2 + 40x - 180 = 0,
解得 x1 = ,x2 = ( 不合题意,舍去 ) .
所以鸡场的面积能达到 180m2 .
设与墙垂直的一边长 x m,则与墙平行的一边长( 40 - 2x)m.
则有 x( 40 - 2x ) = 200,
整理,得 -2x2 + 40x - 2000 = 0,
解得 x1 = x2 = 10 .
所以鸡场的面积能达到 200m2 .
(2) 鸡场的面积能达到 250 m2 吗?
解:设与墙垂直的一边长 x m,则与墙平行的一边长 ( 40 - 2x )m.
则有 x( 40 - 2x ) = 250,
整理,得 -2x2 + 40x - 250 = 0,
由 b2 - 4ac = 402 - 4×2×250 = -100 <0,
可知这个方程无解,
所以鸡场的面积不能达到 250 m2 .
课堂小结
几何图形
与一元二次
方程问题
几何图形
常见几何图形
面积是等量关系.
类 型
课本封面问题
彩条/小路
宽度问题
常采用图形
平移能聚零为
整方便列方程
2.3.2 用公式法求解一元二次方程在实际生活中的应用
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 掌握面积法建立一元二次方程的数学模型.
2. 能运用一元二次方程解决与面积有关的实际问题.
学习目标
某小区规划在一个长 30m、宽 20m 的长方形土地上修建三条等宽的通道,使其中两条与 AB 平行,另外一条与 AD 平行,其余部分种花草,要使每一块花草的面积都为 78m2,那么通道宽应该设计为多少?设通道宽为 xm,则由题意列的方程为____________________。
新课引入
(30-2x)(20-x)=6×78
C
B
D
A
你是怎么想的?
你还有不同方法列方程吗?
某小区规划在一个长 30m、宽 20m 的长方形土地上修建三条等宽的通道,使其中两条与 AB 平行,另外一条与 AD 平行,其余部分种花草,要使每一块花草的面积都为 78m2,那么通道宽应该设计为多少?设通道宽为 x m,则由题意列的方程为____________________。
我列的方程是
30x+20×2x-2x2=30×20-6×78
你能解释这个方程吗?
C
B
D
A
在一块长 16m,宽 12m 的矩形荒地上,要建造一个花园,并使花园所占面积的一半,你能给出设计方案吗?
新知学习
12m
16m
仔细思考,你能给出设计方案吗?
小明的设计方案如图所示,其中花园四周小路的宽度都相等。
12m
16m
你能求出小明设计的方案中小路的宽吗?
12m
16m
解:设小路宽为 x m,则有
( 16 - 2x )( 12 - 2x ) = 12 × 16 ÷ 2,
整理,得 x2 - 14x + 24 = 0,
解得 x1 = 2,x2 = 12 .
小明说他的答案是 2m 或 12m,他的答案对吗?
当 x2 =12 时,小路宽和矩形荒地宽相等,不符合题意,故舍去.
答: 如图,设计小路宽为 2 m
小亮的设计方案如图所示,其中花园每个角上的扇形都相等。
12m
16m
xm
你能帮小亮求出图中的 x 吗?
12m
16m
xm
解:设扇形的半径为 x m,则有
πx2 = 12×16÷2,
解得 x1= ,x2= - < 0 ( 舍去 ).
答: 如图,设计小路宽为 m.
温馨提示
在小明的结果中,小路的宽 12m,符合方程的解,但是荒地的宽为 12m,小路的宽不可能为 12m,因而它不是实际问题的解,应舍去,而小路的宽 2m 符合这个实际问题,所以小路的宽是 2m .
同理,在小亮的结果中 不是实际问题的解,所以圆的半径为 ≈ 5.5m .
用“求根公式法”解一元二次方程时,所得的解不一定符合实际,因此,应用一元二次方程解决实际问题要“检验”.
你还有其他设计方案吗?与小伙伴交流.
针对训练
1. 对于花园设计问题,小颖的设计方案如图所示,你能帮她求出图中 x吗?
12m
16m
x m
x m
解:设小路宽为 x m,则有
( 16 - x )( 12 - x ) = 12 × 16 ÷ 2,
整理,得 x2 - 28x + 96 = 0,
解得 x1 = 4,x2 = 24 ( 不合题意,舍去 ) .
答:小路宽为4 m
12m
16m
x m
x m
2. 在一幅长 90 cm、宽 40 cm 的风景画的四周外围镶上一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂画面积的 72%,那么金色纸边的宽度应该是多少?
解:设金边的宽为 x cm,则有
( 90 + 2x )( 40 + 2x ) × 72% = 90 × 40,
整理,得 x2 + 65x - 350 = 0,
解得 x1 = 5,x2 = -70 ( 不合题意,舍去 ) .
则金色纸边的宽度应该是 5cm.
3. 某农场要建一个长方形的养鸡场,鸡场的一边靠墙 ( 墙长 25 m ),另三边用木栏围成,木栏长 40m.
(1) 鸡场的面积能达到 180 m2 吗?能达到 200 m2 吗?
解:设与墙垂直的一边长 xm,则与墙平行的一边长( 40 - 2x )m.
则有 x( 40 - 2x ) = 180,
整理,得 -2x2 + 40x - 180 = 0,
解得 x1 = ,x2 = ( 不合题意,舍去 ) .
所以鸡场的面积能达到 180m2 .
设与墙垂直的一边长 x m,则与墙平行的一边长( 40 - 2x)m.
则有 x( 40 - 2x ) = 200,
整理,得 -2x2 + 40x - 2000 = 0,
解得 x1 = x2 = 10 .
所以鸡场的面积能达到 200m2 .
(2) 鸡场的面积能达到 250 m2 吗?
解:设与墙垂直的一边长 x m,则与墙平行的一边长 ( 40 - 2x )m.
则有 x( 40 - 2x ) = 250,
整理,得 -2x2 + 40x - 250 = 0,
由 b2 - 4ac = 402 - 4×2×250 = -100 <0,
可知这个方程无解,
所以鸡场的面积不能达到 250 m2 .
课堂小结
几何图形
与一元二次
方程问题
几何图形
常见几何图形
面积是等量关系.
类 型
课本封面问题
彩条/小路
宽度问题
常采用图形
平移能聚零为
整方便列方程
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
