2.4 用因式分解法求解一元二次方程 课件(共26张PPT)
文档属性
| 名称 | 2.4 用因式分解法求解一元二次方程 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 486.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 11:07:43 | ||
图片预览








文档简介
(共26张PPT)
2.4 用因式分解法求解一元二次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 会用因式分解法解一些特殊的一元二次方程.
2. 会根据方程的特点选用恰当的方法解一元二次方程,体会解决问题方法的多样性.
学习目标
我们知道 ab = 0,那么 a = 0 或 b = 0,类似的解方程 (x + 1)(x - 1) = 0 时,可转化为两个一元一次方程 x + 1 = 0 或 x - 1 = 0 来解.
新课引入
你能求
(x + 3)(x-5) = 0 的解吗?
一个数的平方与这个数的 3 倍有可能相等吗?如果相等,这个数是几?你是怎样求出来的?
新知学习
一 因式分解法解一元二次方程
小颖、小明和小亮都设这个数为 x,根据题意,可得方程 x2 = 3x. 但是它们的解法各不相同.
他们做的对吗?为什么?你是怎么做的?
√
×
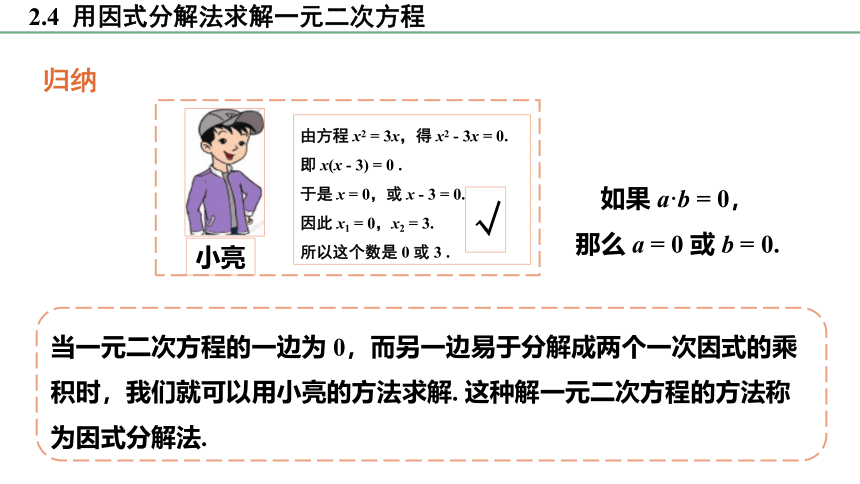
由方程 x2 = 3x,得 x2 - 3x = 0.
因此 x = .
x1 = 0,x2 = 3.
所以这个数是 0 或 3 .
小颖
方程 x2 = 3x 两边同时约去 x,得 x = 3.
所以这个数是 3.
小明
√
由方程 x2 = 3x,得 x2 - 3x = 0.
即 x(x - 3) = 0 .
于是 x = 0,或 x - 3 = 0.
因此 x1 = 0,x2 = 3.
所以这个数是 0 或 3 .
小亮
方程 x2 = 3x 两边同时约去 x,得 x = 3.
所以这个数是 3.
小明的错误,根据等式的基本性质,方程 x2 = 3x 两边同时约去 x 时,必须确保 x ≠ 0,但是这里恰恰能够等于 0,所以这种变形是错误的.
如果 a·b = 0,
那么 a = 0 或 b = 0.
归纳
当一元二次方程的一边为 0,而另一边易于分解成两个一次因式的乘积时,我们就可以用小亮的方法求解. 这种解一元二次方程的方法称为因式分解法.
由方程 x2 = 3x,得 x2 - 3x = 0.
即 x(x - 3) = 0 .
于是 x = 0,或 x - 3 = 0.
因此 x1 = 0,x2 = 3.
所以这个数是 0 或 3 .
√
小亮
例1 解下列方程
(1) 5x2 = 4x
解:(1) 原方程可变形为
5x2 - 4x = 0,
x(5x - 4) = 0.
x = 0,或 5x - 4 = 0.
x1 = 0,x2 = .
(2) x(x - 2) = x - 2
解:(2) 原方程可变形为
x(x - 2) - (x - 2) = 0,
(x - 2)(x - 1) = 0.
x - 2 = 0,或 x - 1 = 0.
x1 = 2,x2 = 1.
原来的一元二次方程转化成了两个一元一次方程
转化思想
降次思想
提公因式法
提公因式法
思考
你能用因式分解法解方程 x2 - 4 = 0,(x + 1)2 - 25 = 0 吗?
解:(1) 原方程可变形为
(x + 2)(x - 2) = 0,
x1 = -2,x2 = 2.
解:(2) 原方程可变形为
(x + 1)2 - 52 = 0
(x + 1 + 5)(x + 1 - 5) = 0
(x - 4)(x + 6) = 0,
x1 = 4,x2 = -6.
公式法---平方差公式
公式法---平方差公式
你还有其他方法吗?
归纳
1. 能够因式分解法的方程的特点:方程右边为 0,左边可以因式分解;
2. 因式分解法解方程的一般步骤:
① 变形为方程右边为 0 的形式;
② 用提公因式法或者是公式法对方程左边因式分解;
③ 方程左边的因式其中至少一个为 0,转化为两个一元一次方程;
④ 解一元一次方程,写出答案;
⑤ 检验.
二 灵活选用方法解方程
例2 用适当的方法解方程:
(1) 3x(x + 5) = 5(x + 5);
分析:该式左右两边可以提取公因式,所以用因式分解法解答较快.
解:(1) 化简,得
(3x -5) (x + 5) = 0.
即 3x - 5 = 0 或 x + 5 = 0.
x1 = ,x2 = -5.
(2) (5x + 1)2 = 1;
分析:方程一边以平方形式出现,另一边是常数,可直接用开平方法.
解: 开平方,得
5x + 1 = ±1.
解得,x1= 0,x2 = .
(3) x2 - 12x = 4;
分析:二次项的系数为 1,可用配方法来解题较快.
解: 配方,得
x2 - 12x + 62 = 4 + 62,
即 (x - 6)2 = 40.
开平方,得
x - 6 = ± .
x1 = 6 + ,x2 = 6 - .
(4) 3x2 = 4 x + 1 ;
分析:二次项的系数不为 1,且不能真接开平方,也不能直接因式分解,所以适合公式法.
解:化为一般形式
3x2 - 4x - 1 = 0
∵Δ = b2 - 4ac = 28 > 0,
∴ .
x1 = ,x2 = .
归纳
填一填:各种一元二次方程的解法及适用类型.
x2 + px + q = 0 ( p2 - 4q ≥0)
(x + m)2 = n (n ≥ 0)
ax2 + bx +c = 0 ( a ≠ 0,b2 - 4ac ≥ 0)
(x + m) (x + n) = 0
针对训练
1. 用适当的方法解方程:
(1) (x + 2)(x - 4) = 0;
解:(1) x + 2 = 0 或 x - 4 = 0.
x1 = -2,x2 = 4.
(2) 4x(2x + 1) = 3(2x + 1);
解:(2) 化简,得
(4x - 3) (2x + 1) = 0.
即 4x - 3 = 0 或 2x + 1 = 0.
x1 = ,x2 = .
2. 一个数平方的 2 倍等于这个数的 7 倍,求这个数.
解:设这个数为 x,根据题意,得 2x2 = 7x.
整理,得
2x2 - 7x = 0.
解得 x1 = 0,x2 = .
所以这个数为 0 或 .
3. 解下列方程:
(1) 5( x2 - x ) = 3( x2 + x )
解:(1) 化简,得
5( x2 - x ) - 3( x2 + x ) = 0
5x( x - 1) - 3x( x + 1 ) = 0
x( 5x - 5 - 3x - 3 ) = 0
x( 2x - 8 ) = 0
即 x = 0 或 2x - 8 = 0.
x1 = 0,x2 = 4.
(2) ( x - 2 )2 = ( 2x + 3 )2
解:(2) 化简,得
( x - 2 )2 - ( 2x + 3 )2 = 0
( x - 2 + 2x + 3 )( x - 2 - 2x - 3 ) = 0
( 3x + 1 )( -x - 5 ) = 0
即 3x + 1 = 0 或 -x - 5 = 0.
x1 = ,x2 = -5.
(3) ( x - 2 )( x - 3 ) = 12
解:(3) 化简,得
( x - 2 )( x - 3 ) -12 = 0
x2 - 5x + 6 - 12 = 0
x2 - 5x - 6 = 0
( x + 1 )( x - 6 ) = 0
即 x + 1 = 0 或 x - 6 = 0.
x1 = -1,x2 = 5.
(4) 2x + 6 = ( x + 3 )2
解:(4) 化简,得
2x + 6 - ( x + 3 )2 = 0
2( x + 3 ) - ( x + 3 )2 = 0
( x + 3 )( 2 - x - 3 ) = 0
( x + 3 )( -x - 1 ) = 0
即 x + 3 = 0 或 -x - 1 = 0.
x1 = -3,x2 = -1.
(5) 2y2 + 4y = y + 2
解:(5) 化简,得
2y( y + 2 ) - ( y +2) = 0
( 2y - 1 )( y + 2 ) = 0
即 2y - 1 = 0 或 y + 2 = 0.
y1 = ,y2 = -2.
课堂小结
1. 因式分解法的概念是什么?
当一元二次方程的一边为 0,而另一边易于分解成两个一次因式的乘积时,我们就可以用因式分解法.
2. 因式分解法的原理是什么?
如果 a·b = 0,那么 a = 0 或 b = 0.
3. 因式分解法的一般步骤是什么?
① 变形为方程右边为 0 的形式;
② 用提公因式法或者是公式法对方程左边因式分解;
③ 方程左边的因式其中至少一个为 0,转化为两个一元一次方程;
④ 解一元一次方程,写出答案;
⑤ 检验.
4. 如何根据方程的特征选择方程的解法?
x2 + px + q = 0 ( p2 - 4q ≥0)
(x + m)2 = n (n ≥ 0)
ax2 + bx +c = 0 ( a ≠ 0,b2 - 4ac ≥ 0)
(x + m) (x + n) = 0
因式分解法
概念
如果a·b = 0,那么 a = 0 或 b = 0.
原理
当一元二次方程的一边为 0,
而另一边易于分解成两个
一次因式的乘积时,我们
就可以用因式分解法.
转化,整体,降次思想
思想
不能直接约去方程两边的因式,
最后结果可以带入检验。
易错点
2.4 用因式分解法求解一元二次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 会用因式分解法解一些特殊的一元二次方程.
2. 会根据方程的特点选用恰当的方法解一元二次方程,体会解决问题方法的多样性.
学习目标
我们知道 ab = 0,那么 a = 0 或 b = 0,类似的解方程 (x + 1)(x - 1) = 0 时,可转化为两个一元一次方程 x + 1 = 0 或 x - 1 = 0 来解.
新课引入
你能求
(x + 3)(x-5) = 0 的解吗?
一个数的平方与这个数的 3 倍有可能相等吗?如果相等,这个数是几?你是怎样求出来的?
新知学习
一 因式分解法解一元二次方程
小颖、小明和小亮都设这个数为 x,根据题意,可得方程 x2 = 3x. 但是它们的解法各不相同.
他们做的对吗?为什么?你是怎么做的?
√
×
由方程 x2 = 3x,得 x2 - 3x = 0.
因此 x = .
x1 = 0,x2 = 3.
所以这个数是 0 或 3 .
小颖
方程 x2 = 3x 两边同时约去 x,得 x = 3.
所以这个数是 3.
小明
√
由方程 x2 = 3x,得 x2 - 3x = 0.
即 x(x - 3) = 0 .
于是 x = 0,或 x - 3 = 0.
因此 x1 = 0,x2 = 3.
所以这个数是 0 或 3 .
小亮
方程 x2 = 3x 两边同时约去 x,得 x = 3.
所以这个数是 3.
小明的错误,根据等式的基本性质,方程 x2 = 3x 两边同时约去 x 时,必须确保 x ≠ 0,但是这里恰恰能够等于 0,所以这种变形是错误的.
如果 a·b = 0,
那么 a = 0 或 b = 0.
归纳
当一元二次方程的一边为 0,而另一边易于分解成两个一次因式的乘积时,我们就可以用小亮的方法求解. 这种解一元二次方程的方法称为因式分解法.
由方程 x2 = 3x,得 x2 - 3x = 0.
即 x(x - 3) = 0 .
于是 x = 0,或 x - 3 = 0.
因此 x1 = 0,x2 = 3.
所以这个数是 0 或 3 .
√
小亮
例1 解下列方程
(1) 5x2 = 4x
解:(1) 原方程可变形为
5x2 - 4x = 0,
x(5x - 4) = 0.
x = 0,或 5x - 4 = 0.
x1 = 0,x2 = .
(2) x(x - 2) = x - 2
解:(2) 原方程可变形为
x(x - 2) - (x - 2) = 0,
(x - 2)(x - 1) = 0.
x - 2 = 0,或 x - 1 = 0.
x1 = 2,x2 = 1.
原来的一元二次方程转化成了两个一元一次方程
转化思想
降次思想
提公因式法
提公因式法
思考
你能用因式分解法解方程 x2 - 4 = 0,(x + 1)2 - 25 = 0 吗?
解:(1) 原方程可变形为
(x + 2)(x - 2) = 0,
x1 = -2,x2 = 2.
解:(2) 原方程可变形为
(x + 1)2 - 52 = 0
(x + 1 + 5)(x + 1 - 5) = 0
(x - 4)(x + 6) = 0,
x1 = 4,x2 = -6.
公式法---平方差公式
公式法---平方差公式
你还有其他方法吗?
归纳
1. 能够因式分解法的方程的特点:方程右边为 0,左边可以因式分解;
2. 因式分解法解方程的一般步骤:
① 变形为方程右边为 0 的形式;
② 用提公因式法或者是公式法对方程左边因式分解;
③ 方程左边的因式其中至少一个为 0,转化为两个一元一次方程;
④ 解一元一次方程,写出答案;
⑤ 检验.
二 灵活选用方法解方程
例2 用适当的方法解方程:
(1) 3x(x + 5) = 5(x + 5);
分析:该式左右两边可以提取公因式,所以用因式分解法解答较快.
解:(1) 化简,得
(3x -5) (x + 5) = 0.
即 3x - 5 = 0 或 x + 5 = 0.
x1 = ,x2 = -5.
(2) (5x + 1)2 = 1;
分析:方程一边以平方形式出现,另一边是常数,可直接用开平方法.
解: 开平方,得
5x + 1 = ±1.
解得,x1= 0,x2 = .
(3) x2 - 12x = 4;
分析:二次项的系数为 1,可用配方法来解题较快.
解: 配方,得
x2 - 12x + 62 = 4 + 62,
即 (x - 6)2 = 40.
开平方,得
x - 6 = ± .
x1 = 6 + ,x2 = 6 - .
(4) 3x2 = 4 x + 1 ;
分析:二次项的系数不为 1,且不能真接开平方,也不能直接因式分解,所以适合公式法.
解:化为一般形式
3x2 - 4x - 1 = 0
∵Δ = b2 - 4ac = 28 > 0,
∴ .
x1 = ,x2 = .
归纳
填一填:各种一元二次方程的解法及适用类型.
x2 + px + q = 0 ( p2 - 4q ≥0)
(x + m)2 = n (n ≥ 0)
ax2 + bx +c = 0 ( a ≠ 0,b2 - 4ac ≥ 0)
(x + m) (x + n) = 0
针对训练
1. 用适当的方法解方程:
(1) (x + 2)(x - 4) = 0;
解:(1) x + 2 = 0 或 x - 4 = 0.
x1 = -2,x2 = 4.
(2) 4x(2x + 1) = 3(2x + 1);
解:(2) 化简,得
(4x - 3) (2x + 1) = 0.
即 4x - 3 = 0 或 2x + 1 = 0.
x1 = ,x2 = .
2. 一个数平方的 2 倍等于这个数的 7 倍,求这个数.
解:设这个数为 x,根据题意,得 2x2 = 7x.
整理,得
2x2 - 7x = 0.
解得 x1 = 0,x2 = .
所以这个数为 0 或 .
3. 解下列方程:
(1) 5( x2 - x ) = 3( x2 + x )
解:(1) 化简,得
5( x2 - x ) - 3( x2 + x ) = 0
5x( x - 1) - 3x( x + 1 ) = 0
x( 5x - 5 - 3x - 3 ) = 0
x( 2x - 8 ) = 0
即 x = 0 或 2x - 8 = 0.
x1 = 0,x2 = 4.
(2) ( x - 2 )2 = ( 2x + 3 )2
解:(2) 化简,得
( x - 2 )2 - ( 2x + 3 )2 = 0
( x - 2 + 2x + 3 )( x - 2 - 2x - 3 ) = 0
( 3x + 1 )( -x - 5 ) = 0
即 3x + 1 = 0 或 -x - 5 = 0.
x1 = ,x2 = -5.
(3) ( x - 2 )( x - 3 ) = 12
解:(3) 化简,得
( x - 2 )( x - 3 ) -12 = 0
x2 - 5x + 6 - 12 = 0
x2 - 5x - 6 = 0
( x + 1 )( x - 6 ) = 0
即 x + 1 = 0 或 x - 6 = 0.
x1 = -1,x2 = 5.
(4) 2x + 6 = ( x + 3 )2
解:(4) 化简,得
2x + 6 - ( x + 3 )2 = 0
2( x + 3 ) - ( x + 3 )2 = 0
( x + 3 )( 2 - x - 3 ) = 0
( x + 3 )( -x - 1 ) = 0
即 x + 3 = 0 或 -x - 1 = 0.
x1 = -3,x2 = -1.
(5) 2y2 + 4y = y + 2
解:(5) 化简,得
2y( y + 2 ) - ( y +2) = 0
( 2y - 1 )( y + 2 ) = 0
即 2y - 1 = 0 或 y + 2 = 0.
y1 = ,y2 = -2.
课堂小结
1. 因式分解法的概念是什么?
当一元二次方程的一边为 0,而另一边易于分解成两个一次因式的乘积时,我们就可以用因式分解法.
2. 因式分解法的原理是什么?
如果 a·b = 0,那么 a = 0 或 b = 0.
3. 因式分解法的一般步骤是什么?
① 变形为方程右边为 0 的形式;
② 用提公因式法或者是公式法对方程左边因式分解;
③ 方程左边的因式其中至少一个为 0,转化为两个一元一次方程;
④ 解一元一次方程,写出答案;
⑤ 检验.
4. 如何根据方程的特征选择方程的解法?
x2 + px + q = 0 ( p2 - 4q ≥0)
(x + m)2 = n (n ≥ 0)
ax2 + bx +c = 0 ( a ≠ 0,b2 - 4ac ≥ 0)
(x + m) (x + n) = 0
因式分解法
概念
如果a·b = 0,那么 a = 0 或 b = 0.
原理
当一元二次方程的一边为 0,
而另一边易于分解成两个
一次因式的乘积时,我们
就可以用因式分解法.
转化,整体,降次思想
思想
不能直接约去方程两边的因式,
最后结果可以带入检验。
易错点
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
