4.4.4 黄金分割 课件(共21张PPT)
文档属性
| 名称 | 4.4.4 黄金分割 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 768.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 20:30:08 | ||
图片预览







文档简介
(共21张PPT)
4.4.4 黄金分割
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 知道并理解黄金分割的定义,熟记黄金比;
2. 能对黄金分割进行简单运用.
学习目标
新课引入
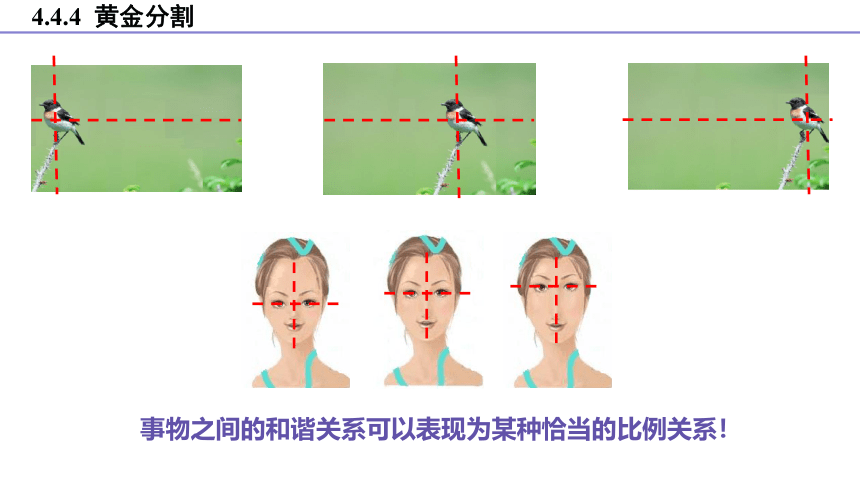
通过观察,你觉得下面那副图最有美感?
事物之间的和谐关系可以表现为某种恰当的比例关系!
一个五角星如图所示.
(1) 从图中找出相等的角、相等的线段.
(2) 在图中找出两对相似比不同的相似三角形.
新知学习
(1) ①∠A =∠K =∠B =∠G =∠E =∠LDC =∠LCD ,
②∠EDF =∠EFD =∠GFH =∠GHF =∠BHC =∠BCH =∠KCL =∠KLC =∠ALD =∠ADL =∠GDC =∠GCD,
③ LD = DF = FH = HC = CL;AD = EF = GH = BC = KL
(2) △GFH = △GDC,△LDC =△LEB.
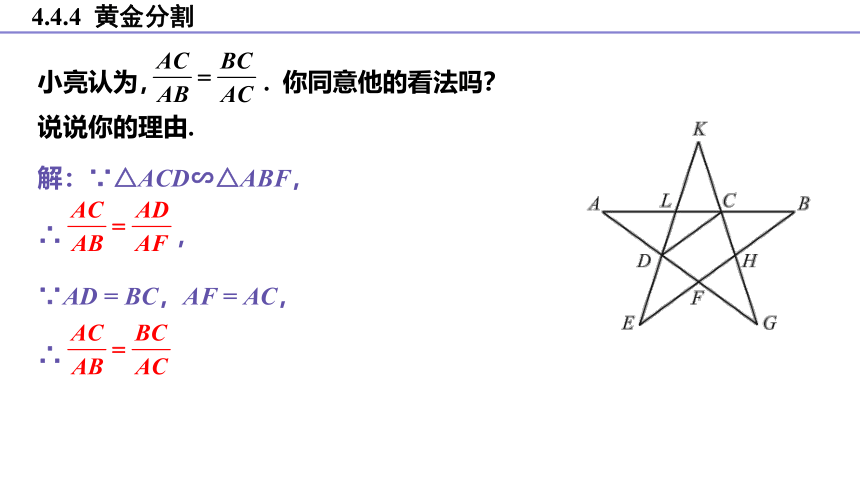
小亮认为, . 你同意他的看法吗?说说你的理由.
解:∵△ACD∽△ABF,
∴ ,
∵AD = BC,AF = AC,
∴
一般地,点 C 把线段 AB 分成两条线段 AC 和 BC ( 如图 ),如果 ,那么称线段 AB 被点 C 黄金分割,点 C 叫做线段 AB 的黄金分割点,AC 与 AB 的比叫做黄金比.
一条线段有几个黄金分割点?
归纳
2个
例1 计算黄金比.
解:由 ,得 AC2 = AB · BC.
设 AB = 1,AC = x,则 BC = 1 – x .
∴x2 = 1×( 1 – x ),
即 x2 + x – 1 = 0.
解这个方程,得
( 不合题意,舍去 ).
所以,黄金比 .
上图是古希腊时期的巴台农神庙,如果把左图中用虚线表示的矩形画成右图中的矩形 ABCD,以矩形 ABCD 的宽为边在其内部作正方形 AEFD,那么我们可以惊奇地发现, 点 E 是 AB 的黄金分割点吗?矩形ABCD 的宽与长的比是黄金比吗?
思考
由 ,可得 ,即 ,因此点 E 是 AB 的黄金分割点.
( 即 ) 是黄金比,也就是说矩形 ABCD 的宽与长的比是黄金比.
例2 采用如下方法可以得到黄金分割点:如图,设 AB 是已知线段,过点 B 作 BD⊥AB,使 ;连接 AD,在 AD 上截取 DE = DB;在 AB 上截取 AC = AE . 点 C 就是线段 AB 的黄金分割点. 你能说出其中的道理吗?
A
B
D
E
C
设 AB = 1,则 BD = .
由勾股定理得 AD = = ,
∴ AC = AE = ,从而点 C 是 AB 的黄金分割点.
A
B
D
E
C
1. 在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近 0.618 越给人以美感. 小明的妈妈脚底到肚脐的长度与身高的比为 0.60,她的身高为 1.60 m,她应该穿多高的高跟鞋看起来会更美?
针对训练
解:设肚脐到脚底的距离为 x m,
根据题意,得 ,解得 x = 0.96.
设穿上 y m 高的高跟鞋看起来会更美,则
解得 y ≈ 0.075,而 0.075m = 7.5 cm.
故她应该穿约为 7.5 cm 高的高跟鞋看起来会更美.
2. 如图:在△ABC 中,AB = AC,∠BAC = 36°, BD 平分∠ABC 交 AC 于点 D,求证:D 是 AC 的黄金分割点.
证明:在等腰△ABC 中,顶角∠A = 36°,
所以∠ABC =∠C = 72°,
∵BD 为∠ABC 的平分线,∴∠ABD =∠DBC = 36°,
在△ACB 和△BCD 中,∠BDC = 72°,
∵∠C =∠C,∠A =∠CBD = 36°,∴△ACB∽△BCD,
∴AC : BC = BC : DC;
A
B
D
C
∵∠A =∠ABD,
∴AD = BD.
∵∠DBC = 36°,∠C = 72°,
∴∠BDC = 72°,
∴BD = BC,
∴AD = BC,
∴AC : AD = AD : DC;
即点 D 是 AC 的黄金分割点.
A
B
D
C
3. 如图,设 AB 是已知线段,在 AB 上作正方形 ABCD;取 AD 的中点 E,连接 EB;延长 DA 至 F,使 EF = EB;以线段 AF 为边作正方形AFGH. 点 H 就是 AB 的黄金分割点. 你能说出这种作法的道理吗?
证明:设 AB = 1,那么在 Rt△BAE 中,
,
于是 EF = BE = ,
AH = AF = BE - AE = = .
BH = AB - AH = = .
因此 = ,点 H 就是 AB 的黄金分割点.
1. 什么叫做黄金分割?黄金比是多少?
2. 一条线段有几个黄金分割点?
课堂小结
一般地,点 C 把线段 AB 分成两条线段 AC 和 BC ,如果 ,那么称线段 AB 被点 C 黄金分割,点 C 叫做线段 AB 的黄金分割点,AC 与 AB 的比叫做黄金比.
2个
3. 如何用尺规作线段的黄金分割点和黄金矩形?
设 AB 是已知线段,过点 B 作 BD⊥AB,使 ;连接 AD,在 AD 上截取 DE = DB;在 AB 上截取 AC = AE . 点 C 就是线段 AB 的黄金分割点.
4.黄金分割有关的值.
较长
最短
最长
4.4.4 黄金分割
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 知道并理解黄金分割的定义,熟记黄金比;
2. 能对黄金分割进行简单运用.
学习目标
新课引入
通过观察,你觉得下面那副图最有美感?
事物之间的和谐关系可以表现为某种恰当的比例关系!
一个五角星如图所示.
(1) 从图中找出相等的角、相等的线段.
(2) 在图中找出两对相似比不同的相似三角形.
新知学习
(1) ①∠A =∠K =∠B =∠G =∠E =∠LDC =∠LCD ,
②∠EDF =∠EFD =∠GFH =∠GHF =∠BHC =∠BCH =∠KCL =∠KLC =∠ALD =∠ADL =∠GDC =∠GCD,
③ LD = DF = FH = HC = CL;AD = EF = GH = BC = KL
(2) △GFH = △GDC,△LDC =△LEB.
小亮认为, . 你同意他的看法吗?说说你的理由.
解:∵△ACD∽△ABF,
∴ ,
∵AD = BC,AF = AC,
∴
一般地,点 C 把线段 AB 分成两条线段 AC 和 BC ( 如图 ),如果 ,那么称线段 AB 被点 C 黄金分割,点 C 叫做线段 AB 的黄金分割点,AC 与 AB 的比叫做黄金比.
一条线段有几个黄金分割点?
归纳
2个
例1 计算黄金比.
解:由 ,得 AC2 = AB · BC.
设 AB = 1,AC = x,则 BC = 1 – x .
∴x2 = 1×( 1 – x ),
即 x2 + x – 1 = 0.
解这个方程,得
( 不合题意,舍去 ).
所以,黄金比 .
上图是古希腊时期的巴台农神庙,如果把左图中用虚线表示的矩形画成右图中的矩形 ABCD,以矩形 ABCD 的宽为边在其内部作正方形 AEFD,那么我们可以惊奇地发现, 点 E 是 AB 的黄金分割点吗?矩形ABCD 的宽与长的比是黄金比吗?
思考
由 ,可得 ,即 ,因此点 E 是 AB 的黄金分割点.
( 即 ) 是黄金比,也就是说矩形 ABCD 的宽与长的比是黄金比.
例2 采用如下方法可以得到黄金分割点:如图,设 AB 是已知线段,过点 B 作 BD⊥AB,使 ;连接 AD,在 AD 上截取 DE = DB;在 AB 上截取 AC = AE . 点 C 就是线段 AB 的黄金分割点. 你能说出其中的道理吗?
A
B
D
E
C
设 AB = 1,则 BD = .
由勾股定理得 AD = = ,
∴ AC = AE = ,从而点 C 是 AB 的黄金分割点.
A
B
D
E
C
1. 在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近 0.618 越给人以美感. 小明的妈妈脚底到肚脐的长度与身高的比为 0.60,她的身高为 1.60 m,她应该穿多高的高跟鞋看起来会更美?
针对训练
解:设肚脐到脚底的距离为 x m,
根据题意,得 ,解得 x = 0.96.
设穿上 y m 高的高跟鞋看起来会更美,则
解得 y ≈ 0.075,而 0.075m = 7.5 cm.
故她应该穿约为 7.5 cm 高的高跟鞋看起来会更美.
2. 如图:在△ABC 中,AB = AC,∠BAC = 36°, BD 平分∠ABC 交 AC 于点 D,求证:D 是 AC 的黄金分割点.
证明:在等腰△ABC 中,顶角∠A = 36°,
所以∠ABC =∠C = 72°,
∵BD 为∠ABC 的平分线,∴∠ABD =∠DBC = 36°,
在△ACB 和△BCD 中,∠BDC = 72°,
∵∠C =∠C,∠A =∠CBD = 36°,∴△ACB∽△BCD,
∴AC : BC = BC : DC;
A
B
D
C
∵∠A =∠ABD,
∴AD = BD.
∵∠DBC = 36°,∠C = 72°,
∴∠BDC = 72°,
∴BD = BC,
∴AD = BC,
∴AC : AD = AD : DC;
即点 D 是 AC 的黄金分割点.
A
B
D
C
3. 如图,设 AB 是已知线段,在 AB 上作正方形 ABCD;取 AD 的中点 E,连接 EB;延长 DA 至 F,使 EF = EB;以线段 AF 为边作正方形AFGH. 点 H 就是 AB 的黄金分割点. 你能说出这种作法的道理吗?
证明:设 AB = 1,那么在 Rt△BAE 中,
,
于是 EF = BE = ,
AH = AF = BE - AE = = .
BH = AB - AH = = .
因此 = ,点 H 就是 AB 的黄金分割点.
1. 什么叫做黄金分割?黄金比是多少?
2. 一条线段有几个黄金分割点?
课堂小结
一般地,点 C 把线段 AB 分成两条线段 AC 和 BC ,如果 ,那么称线段 AB 被点 C 黄金分割,点 C 叫做线段 AB 的黄金分割点,AC 与 AB 的比叫做黄金比.
2个
3. 如何用尺规作线段的黄金分割点和黄金矩形?
设 AB 是已知线段,过点 B 作 BD⊥AB,使 ;连接 AD,在 AD 上截取 DE = DB;在 AB 上截取 AC = AE . 点 C 就是线段 AB 的黄金分割点.
4.黄金分割有关的值.
较长
最短
最长
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
