4.6 利用相似三角形测高 课件(共22张PPT)
文档属性
| 名称 | 4.6 利用相似三角形测高 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 20:56:12 | ||
图片预览





文档简介
(共22张PPT)
4.6 利用相似三角形测高
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
学习目标
1.通过测量旗杆的高度的活动,并复习巩固相似三角形有关知识.
2.灵活运用三角形相似的知识解决实际问题.
新课引入
对于下图这些高大的物体,我们如何测量高度呢?
1. 你还记得利用全等三角形测距离吗?
2. 你还能利用全等三角形测这些物体的高度吗?
新知学习
学校有一根旗杆,同学们好奇旗杆的高度,老师决定借此机会进行一节实践课让大家测量旗杆高度
活动课题:利用相似三角形的有关知识测量旗杆的高度
活动方式:分组活动、全班交流研讨
活动工具:小镜子、标杆、皮尺等测量工具
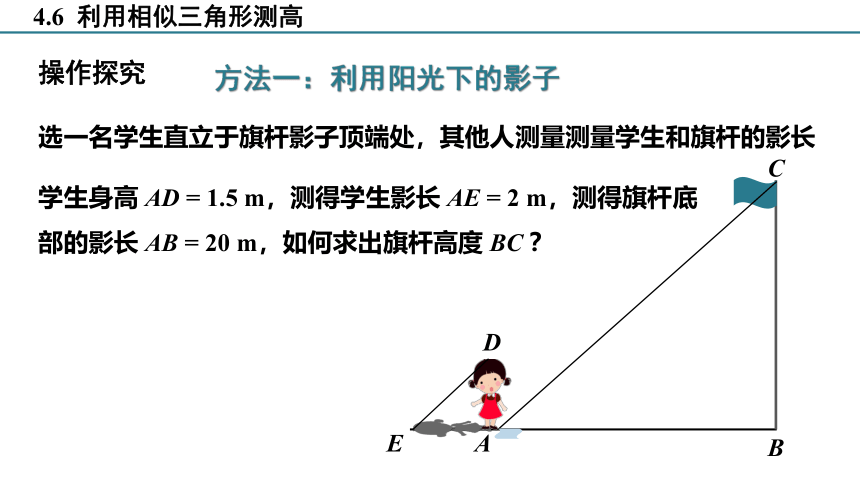
方法一:利用阳光下的影子
学生身高 AD = 1.5 m,测得学生影长 AE = 2 m,测得旗杆底部的影长 AB = 20 m,如何求出旗杆高度 BC ?
A
B
C
D
E
选一名学生直立于旗杆影子顶端处,其他人测量测量学生和旗杆的影长
操作探究
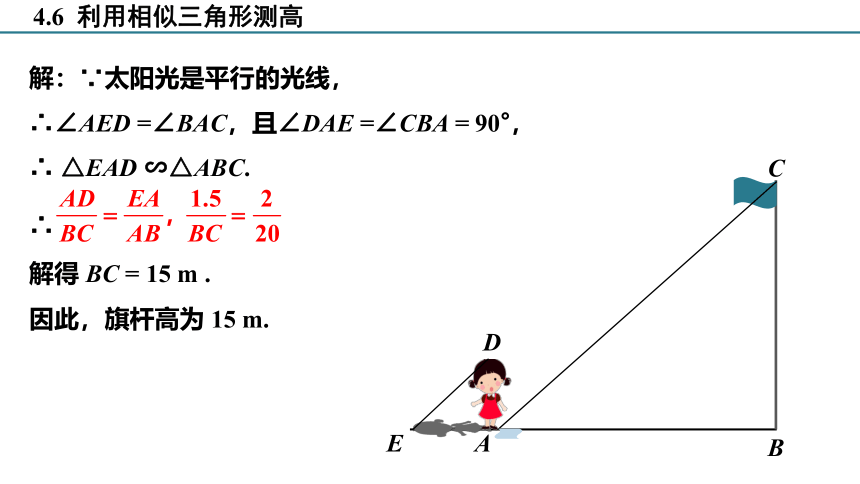
解:∵太阳光是平行的光线,
∴∠AED =∠BAC,且∠DAE =∠CBA = 90°,
∴ △EAD ∽△ABC.
∴
解得 BC = 15 m .
因此,旗杆高为 15 m.
A
B
C
D
E
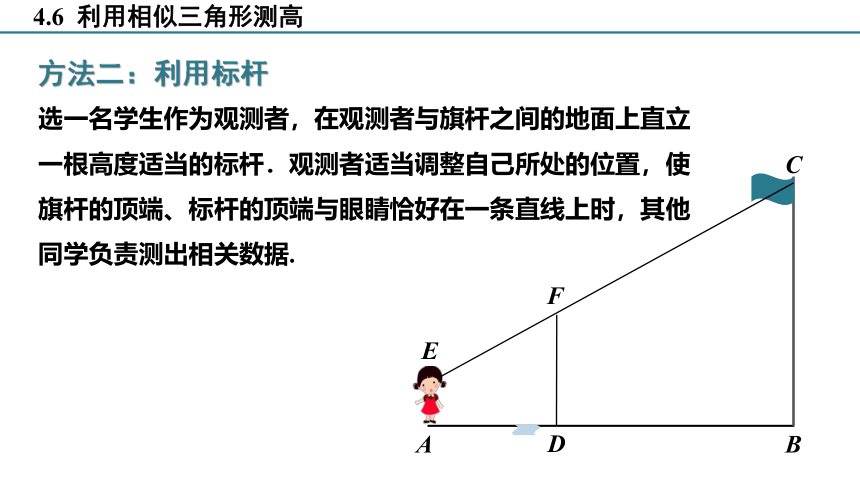
方法二:利用标杆
A
B
C
D
E
F
选一名学生作为观测者,在观测者与旗杆之间的地面上直立一根高度适当的标杆.观测者适当调整自己所处的位置,使旗杆的顶端、标杆的顶端与眼睛恰好在一条直线上时,其他同学负责测出相关数据.
A
B
C
D
E
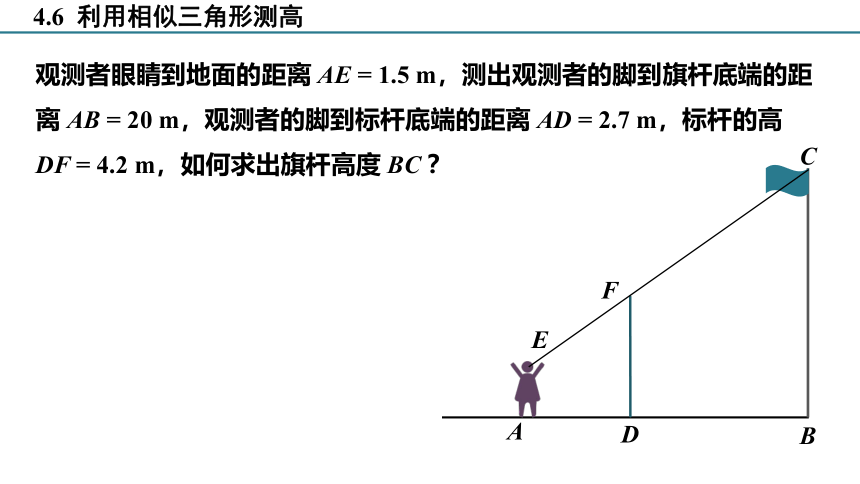
观测者眼睛到地面的距离 AE = 1.5 m,测出观测者的脚到旗杆底端的距离 AB = 20 m,观测者的脚到标杆底端的距离 AD = 2.7 m,标杆的高DF = 4.2 m,如何求出旗杆高度 BC ?
F
过点 E 作 EN∥AB 交 CB 于 N,交 FD 于 M.
∵∠FME =∠CNE = 90°,∠FEM =∠CEN,
∴△EFM ∽△ECN .
∴
∴CN = 13.5 m.
∴BC = 13.5 + 1.5 = 15 m.
因此,旗杆高为 15 m.
A
B
C
D
E
F
N
M
方法三:利用镜子的反射
选一名同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记,观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合. 其他同学负责测出相关数据.
B
C
D
E
A
观测者眼睛到地面的距离 DE = 1.5 m,测出观测者的脚到镜子标记处的距离 AD = 2 m,旗杆底端到镜子标记处的距离 AB = 20 m,如何求出旗杆高度 BC ?
A
B
C
D
E
这里引入一个物理知识:入射角等于反射角
解:∵∠DAE =∠BAC,∠DCE =∠BAE = 90°,
∴△ADE ∽△ABC.
∴ .
解得 BC = 15 m.
因此,旗杆高为 15m.
A
B
C
D
E
思考讨论
你还有哪些测量旗杆高度的方法?
上述几种测量方法各有哪些优缺点?
针对训练
1. 某天同时同地,甲同学测得 1 m 的测竿在地面上影长为 0.8 m,乙同学测得国旗旗杆在地面上的影长为 9.6 m,则国旗旗杆的长为 ( )
A. 10 m B. 12 m C. 13 m D. 15 m
B
A. 4 cm
B. 5 cm
C. 6 cm
D. 8 cm
2. 如图,有一点光源 S 在平面镜上方,若点 P 恰好在点光源 S 的反射光线上,并测得 AB = 10 cm,BC = 20 cm,PC⊥AC,且 PC = 12 cm,则点光源 S 到平面镜的距离 SA 的长度为 ( )
C
3. 如图,小明为了测量一棵树 CD 的高度,他在距树 24 m 处立了一根高为 2 m 的标杆 EF,然后小明前后调整自己的位置,当他与树相距 27 m 的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上. 已知小明的眼高 1.6 m,求树的高度.
A
E
D
F
B
N
M
C
解:过点 A 作 AN∥BD 交 CD 于 N,交 EF 于 M,∠ABF =∠EFD =∠CDF = 90°,
∴AB∥EF∥CD,
∴∠EMA =∠CNA.
∵∠EAM =∠CAN,
∴△AEM∽△ACN,
∴ .
A
E
D
F
B
N
M
C
A
E
D
F
B
N
M
∵AB = 1.6 m ,EF = 2 m , BD = 27 m ,FD = 24 m ,
∴ ,
∴CN = 3.6 m,
∴CD = 3.6 + 1.6 = 5.2 m.
故树的高度为 5.2 m.
C
4. 如图,A、B 两点分别位于一个池塘的两端,小芳想用绳子测量 A、B 两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达 A、B 点的点 C,找到 AC、BC 的中点 D、E,并且 DE 的长为 5 m,则 A、B 两点的距离是多少?
解:∵点 D 与点 E 分别是 AC、BC 的中点,
∴所以 CD = AC,CE = BC,
又∵∠C = ∠C,
∴△CDE∽△CAB,且相似比为 .
∴DE = AB,
即 AB = 2DE = 2×5 = 10 m.
课堂小结
利用阳光下的影子
利用相似三
角形测高
利用镜子的反射
利用标杆
4.6 利用相似三角形测高
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
学习目标
1.通过测量旗杆的高度的活动,并复习巩固相似三角形有关知识.
2.灵活运用三角形相似的知识解决实际问题.
新课引入
对于下图这些高大的物体,我们如何测量高度呢?
1. 你还记得利用全等三角形测距离吗?
2. 你还能利用全等三角形测这些物体的高度吗?
新知学习
学校有一根旗杆,同学们好奇旗杆的高度,老师决定借此机会进行一节实践课让大家测量旗杆高度
活动课题:利用相似三角形的有关知识测量旗杆的高度
活动方式:分组活动、全班交流研讨
活动工具:小镜子、标杆、皮尺等测量工具
方法一:利用阳光下的影子
学生身高 AD = 1.5 m,测得学生影长 AE = 2 m,测得旗杆底部的影长 AB = 20 m,如何求出旗杆高度 BC ?
A
B
C
D
E
选一名学生直立于旗杆影子顶端处,其他人测量测量学生和旗杆的影长
操作探究
解:∵太阳光是平行的光线,
∴∠AED =∠BAC,且∠DAE =∠CBA = 90°,
∴ △EAD ∽△ABC.
∴
解得 BC = 15 m .
因此,旗杆高为 15 m.
A
B
C
D
E
方法二:利用标杆
A
B
C
D
E
F
选一名学生作为观测者,在观测者与旗杆之间的地面上直立一根高度适当的标杆.观测者适当调整自己所处的位置,使旗杆的顶端、标杆的顶端与眼睛恰好在一条直线上时,其他同学负责测出相关数据.
A
B
C
D
E
观测者眼睛到地面的距离 AE = 1.5 m,测出观测者的脚到旗杆底端的距离 AB = 20 m,观测者的脚到标杆底端的距离 AD = 2.7 m,标杆的高DF = 4.2 m,如何求出旗杆高度 BC ?
F
过点 E 作 EN∥AB 交 CB 于 N,交 FD 于 M.
∵∠FME =∠CNE = 90°,∠FEM =∠CEN,
∴△EFM ∽△ECN .
∴
∴CN = 13.5 m.
∴BC = 13.5 + 1.5 = 15 m.
因此,旗杆高为 15 m.
A
B
C
D
E
F
N
M
方法三:利用镜子的反射
选一名同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记,观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合. 其他同学负责测出相关数据.
B
C
D
E
A
观测者眼睛到地面的距离 DE = 1.5 m,测出观测者的脚到镜子标记处的距离 AD = 2 m,旗杆底端到镜子标记处的距离 AB = 20 m,如何求出旗杆高度 BC ?
A
B
C
D
E
这里引入一个物理知识:入射角等于反射角
解:∵∠DAE =∠BAC,∠DCE =∠BAE = 90°,
∴△ADE ∽△ABC.
∴ .
解得 BC = 15 m.
因此,旗杆高为 15m.
A
B
C
D
E
思考讨论
你还有哪些测量旗杆高度的方法?
上述几种测量方法各有哪些优缺点?
针对训练
1. 某天同时同地,甲同学测得 1 m 的测竿在地面上影长为 0.8 m,乙同学测得国旗旗杆在地面上的影长为 9.6 m,则国旗旗杆的长为 ( )
A. 10 m B. 12 m C. 13 m D. 15 m
B
A. 4 cm
B. 5 cm
C. 6 cm
D. 8 cm
2. 如图,有一点光源 S 在平面镜上方,若点 P 恰好在点光源 S 的反射光线上,并测得 AB = 10 cm,BC = 20 cm,PC⊥AC,且 PC = 12 cm,则点光源 S 到平面镜的距离 SA 的长度为 ( )
C
3. 如图,小明为了测量一棵树 CD 的高度,他在距树 24 m 处立了一根高为 2 m 的标杆 EF,然后小明前后调整自己的位置,当他与树相距 27 m 的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上. 已知小明的眼高 1.6 m,求树的高度.
A
E
D
F
B
N
M
C
解:过点 A 作 AN∥BD 交 CD 于 N,交 EF 于 M,∠ABF =∠EFD =∠CDF = 90°,
∴AB∥EF∥CD,
∴∠EMA =∠CNA.
∵∠EAM =∠CAN,
∴△AEM∽△ACN,
∴ .
A
E
D
F
B
N
M
C
A
E
D
F
B
N
M
∵AB = 1.6 m ,EF = 2 m , BD = 27 m ,FD = 24 m ,
∴ ,
∴CN = 3.6 m,
∴CD = 3.6 + 1.6 = 5.2 m.
故树的高度为 5.2 m.
C
4. 如图,A、B 两点分别位于一个池塘的两端,小芳想用绳子测量 A、B 两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达 A、B 点的点 C,找到 AC、BC 的中点 D、E,并且 DE 的长为 5 m,则 A、B 两点的距离是多少?
解:∵点 D 与点 E 分别是 AC、BC 的中点,
∴所以 CD = AC,CE = BC,
又∵∠C = ∠C,
∴△CDE∽△CAB,且相似比为 .
∴DE = AB,
即 AB = 2DE = 2×5 = 10 m.
课堂小结
利用阳光下的影子
利用相似三
角形测高
利用镜子的反射
利用标杆
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
