4.7.1 相似三角形中对应线段的性质 课件(共20张PPT)
文档属性
| 名称 | 4.7.1 相似三角形中对应线段的性质 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 340.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-24 20:54:58 | ||
图片预览




文档简介
(共20张PPT)
4.7.1 相似三角形中对应线段的性质
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 明确相似三角形中对应线段与相似比的关系.
2. 能熟练运用相似三角形的性质解决实际问题.
学习目标
新课引入
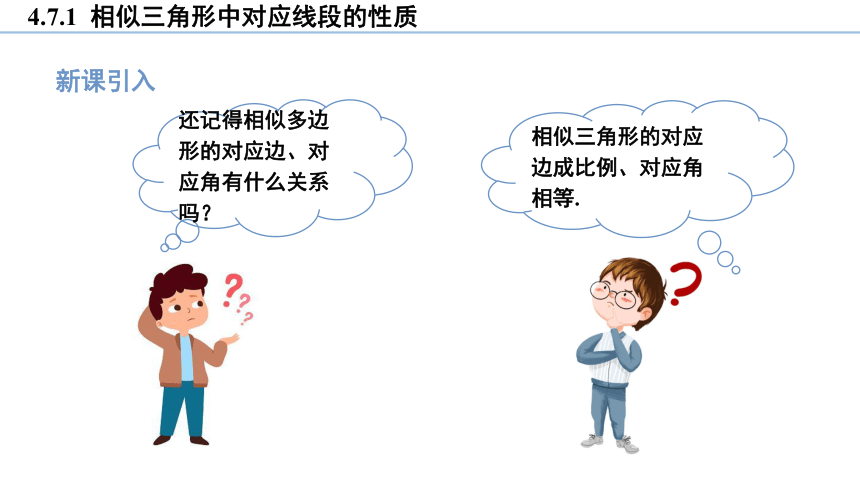
还记得相似多边形的对应边、对应角有什么关系吗?
相似三角形的对应边成比例、对应角相等.
在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢?
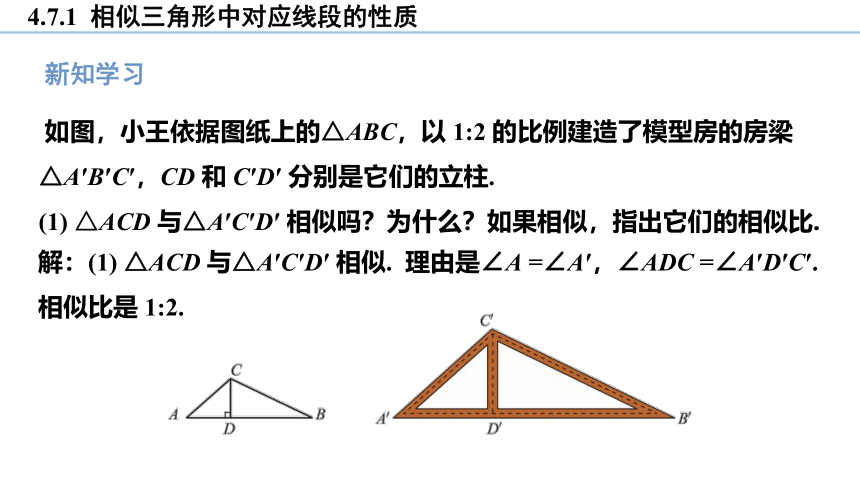
如图,小王依据图纸上的△ABC,以 1:2 的比例建造了模型房的房梁△A′B′C′,CD 和 C′D′ 分别是它们的立柱.
(1) △ACD 与△A′C′D′ 相似吗?为什么?如果相似,指出它们的相似比.
新知学习
解:(1) △ACD 与△A′C′D′ 相似. 理由是∠A =∠A′,∠ADC =∠A′D′C′. 相似比是 1:2.
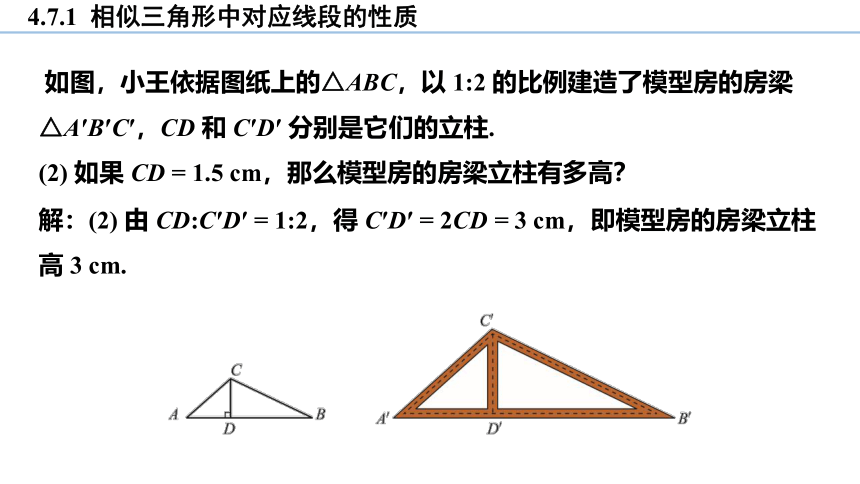
如图,小王依据图纸上的△ABC,以 1:2 的比例建造了模型房的房梁△A′B′C′,CD 和 C′D′ 分别是它们的立柱.
(2) 如果 CD = 1.5 cm,那么模型房的房梁立柱有多高?
解:(2) 由 CD:C′D′ = 1:2,得 C′D′ = 2CD = 3 cm,即模型房的房梁立柱高 3 cm.
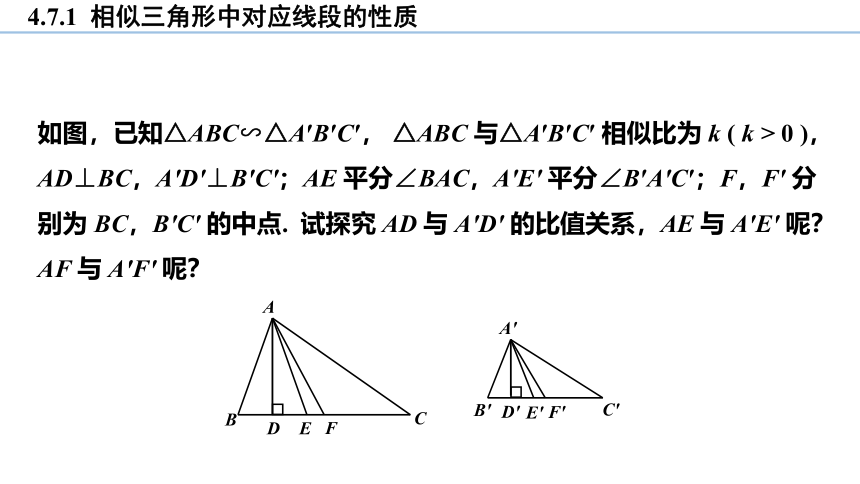
如图,已知△ABC∽△A′B′C′, △ABC 与△A′B′C′ 相似比为 k ( k > 0 ),AD⊥BC,A′D′⊥B′C′;AE 平分∠BAC,A′E′ 平分∠B′A′C′;F,F′ 分别为 BC,B′C′ 的中点. 试探究 AD 与 A′D′ 的比值关系,AE 与 A′E′ 呢?AF 与 A′F′ 呢?
A
B
C
D
E
A′
B′
C′
D′
E′
F
F′
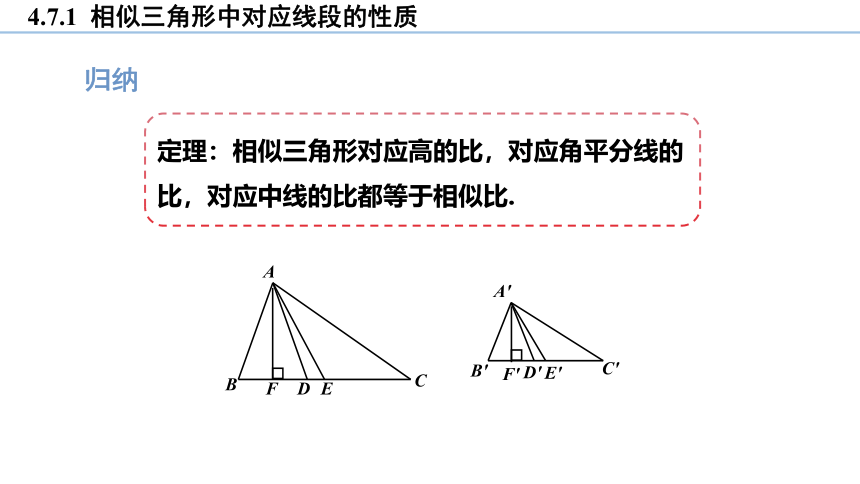
定理:相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比.
归纳
A
B
C
D
E
A′
B′
C′
D′
E′
F
F′
符号语言:
∵△ABC∽△A′B′C′,
且AD⊥BC ,A′D′⊥B′C′ ;
∴AD : A′D′ = k.
A
B
C
D
E
A′
B′
C′
D′
E′
F
F′
符号语言:
∵△ABC∽△A′B′C′,
且∠BAE =∠EAC,∠B′A′E′ =∠E′A′C′,
∴AE : A′E′ = k.
符号语言:
∵△ABC∽△A′B′C′,
且 BF = FC,B′F′ = F′C′,
∴AF : A′F′ = k.
温馨提示
这些结论以后在解决问题过程中能作为定理直接用.
如图,已知△ABC∽△A′B′C′ ,△ABC 与△A′B′C′ 的相似比为 k( k >0 ), 点 D,E 在 BC 边上,点 D′,E′ 在 B′C′ 边上 .
(1) 若∠BAD = ∠BAC,∠B′A′D′ = ∠B′A′C′,则 等于多少?
解:由“两角分别相等的两个三角形相似”,可知△ABD∽△A′B′D′,于是 = = k ( k > 0 ).
拓展迁移
如图,已知△ABC∽△A′B′C′ ,△ABC 与△A′B′C′ 的相似比为 k( k >0 ), 点 D,E 在 BC 边上,点 D′,E′ 在 B′C′ 边上 .
(2) 若 BE = BC , B′E′ = B′C′ ,则 等于多少?
解:由“两边成比例且夹角相等的两个三角形相似”,可知△ABE∽△A′B′E′,于是 = = k ( k > 0 ).
例 如图,AD 是△ABC 的高,点 P,Q 在 BC 边上,点 R 在 AC 边上,点 S 在 AB 边上,BC = 60 cm,AD = 40 cm,四边形 PQRS 是正方形.
(1) △ASR 与△ABC 相似吗?为什么?
A
B
C
S
R
E
P
D
Q
解:△ASR∽△ABC;理由如下:
∵四边形 PQRS 是正方形,
∴RS∥BC.
∴∠ASR =∠B,∠ARS =∠C.
∴△ASR∽△ABC.
例 如图,AD 是△ABC 的高,点 P,Q 在 BC 边上,点 R 在 AC 边上,点 S 在 AB 边上,BC = 60 cm,AD = 40 cm,四边形 PQRS 是正方形.
(2) 求正方形 PQRS 的边长.
解:∵△ASR∽△ABC,
∴ = ,
设正方形 PQRS 的边长为 x cm,则 AE = ( 40 – x ) cm,
∴ . 解得 x = 24 .
答:正方形 PQRS 的边长为 24 cm.
A
B
C
S
R
E
P
D
Q
1. 若△ABC ∽△A'B'C',AD、A'D' 分别是△ABC、△A'B'C' 的高,AD:A'D' = 3:4,△A'B'C' 的一条中线 B'E' = 16 cm,则△ABC 的中线 BE = ________cm.
针对训练
12
2. 两个相似三角形的一组对应角平分线的长分别是 2 cm 和 5 cm,求这两个三角形的相似比. 在这两个三角形的一组对应中线中,如果较短的中线是 3 cm,那么较长的中线多长?
解:∵这两个三角形的相似比是 2 : 5,较短的中线是 3 cm,
∴较长的中线为 3 × = 7.5 cm.
3. 已知△ABC∽△DEF,BG、EH 分△ABC 和△DEF 的角平分线,BC = 6 cm,EF = 4 cm,BG = 4.8 cm. 求 EH 的长.
A
G
B
C
D
E
F
H
解:∵ △ABC∽△DEF,
∴ ,
∴ ,
解得 EH = 3.2 ( cm ).
答:EH 的长为 3.2 cm.
课堂小结
相似三角形的性质
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
一块直角三角形木板的一条直角边 AB 长为 1.5 m,面积为 1.5 m2,要把它加工成一个面积尽可能大的正方形桌面,请同学们设计加工方法.
A
B
C
实践与拓展
4.7.1 相似三角形中对应线段的性质
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 明确相似三角形中对应线段与相似比的关系.
2. 能熟练运用相似三角形的性质解决实际问题.
学习目标
新课引入
还记得相似多边形的对应边、对应角有什么关系吗?
相似三角形的对应边成比例、对应角相等.
在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢?
如图,小王依据图纸上的△ABC,以 1:2 的比例建造了模型房的房梁△A′B′C′,CD 和 C′D′ 分别是它们的立柱.
(1) △ACD 与△A′C′D′ 相似吗?为什么?如果相似,指出它们的相似比.
新知学习
解:(1) △ACD 与△A′C′D′ 相似. 理由是∠A =∠A′,∠ADC =∠A′D′C′. 相似比是 1:2.
如图,小王依据图纸上的△ABC,以 1:2 的比例建造了模型房的房梁△A′B′C′,CD 和 C′D′ 分别是它们的立柱.
(2) 如果 CD = 1.5 cm,那么模型房的房梁立柱有多高?
解:(2) 由 CD:C′D′ = 1:2,得 C′D′ = 2CD = 3 cm,即模型房的房梁立柱高 3 cm.
如图,已知△ABC∽△A′B′C′, △ABC 与△A′B′C′ 相似比为 k ( k > 0 ),AD⊥BC,A′D′⊥B′C′;AE 平分∠BAC,A′E′ 平分∠B′A′C′;F,F′ 分别为 BC,B′C′ 的中点. 试探究 AD 与 A′D′ 的比值关系,AE 与 A′E′ 呢?AF 与 A′F′ 呢?
A
B
C
D
E
A′
B′
C′
D′
E′
F
F′
定理:相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比.
归纳
A
B
C
D
E
A′
B′
C′
D′
E′
F
F′
符号语言:
∵△ABC∽△A′B′C′,
且AD⊥BC ,A′D′⊥B′C′ ;
∴AD : A′D′ = k.
A
B
C
D
E
A′
B′
C′
D′
E′
F
F′
符号语言:
∵△ABC∽△A′B′C′,
且∠BAE =∠EAC,∠B′A′E′ =∠E′A′C′,
∴AE : A′E′ = k.
符号语言:
∵△ABC∽△A′B′C′,
且 BF = FC,B′F′ = F′C′,
∴AF : A′F′ = k.
温馨提示
这些结论以后在解决问题过程中能作为定理直接用.
如图,已知△ABC∽△A′B′C′ ,△ABC 与△A′B′C′ 的相似比为 k( k >0 ), 点 D,E 在 BC 边上,点 D′,E′ 在 B′C′ 边上 .
(1) 若∠BAD = ∠BAC,∠B′A′D′ = ∠B′A′C′,则 等于多少?
解:由“两角分别相等的两个三角形相似”,可知△ABD∽△A′B′D′,于是 = = k ( k > 0 ).
拓展迁移
如图,已知△ABC∽△A′B′C′ ,△ABC 与△A′B′C′ 的相似比为 k( k >0 ), 点 D,E 在 BC 边上,点 D′,E′ 在 B′C′ 边上 .
(2) 若 BE = BC , B′E′ = B′C′ ,则 等于多少?
解:由“两边成比例且夹角相等的两个三角形相似”,可知△ABE∽△A′B′E′,于是 = = k ( k > 0 ).
例 如图,AD 是△ABC 的高,点 P,Q 在 BC 边上,点 R 在 AC 边上,点 S 在 AB 边上,BC = 60 cm,AD = 40 cm,四边形 PQRS 是正方形.
(1) △ASR 与△ABC 相似吗?为什么?
A
B
C
S
R
E
P
D
Q
解:△ASR∽△ABC;理由如下:
∵四边形 PQRS 是正方形,
∴RS∥BC.
∴∠ASR =∠B,∠ARS =∠C.
∴△ASR∽△ABC.
例 如图,AD 是△ABC 的高,点 P,Q 在 BC 边上,点 R 在 AC 边上,点 S 在 AB 边上,BC = 60 cm,AD = 40 cm,四边形 PQRS 是正方形.
(2) 求正方形 PQRS 的边长.
解:∵△ASR∽△ABC,
∴ = ,
设正方形 PQRS 的边长为 x cm,则 AE = ( 40 – x ) cm,
∴ . 解得 x = 24 .
答:正方形 PQRS 的边长为 24 cm.
A
B
C
S
R
E
P
D
Q
1. 若△ABC ∽△A'B'C',AD、A'D' 分别是△ABC、△A'B'C' 的高,AD:A'D' = 3:4,△A'B'C' 的一条中线 B'E' = 16 cm,则△ABC 的中线 BE = ________cm.
针对训练
12
2. 两个相似三角形的一组对应角平分线的长分别是 2 cm 和 5 cm,求这两个三角形的相似比. 在这两个三角形的一组对应中线中,如果较短的中线是 3 cm,那么较长的中线多长?
解:∵这两个三角形的相似比是 2 : 5,较短的中线是 3 cm,
∴较长的中线为 3 × = 7.5 cm.
3. 已知△ABC∽△DEF,BG、EH 分△ABC 和△DEF 的角平分线,BC = 6 cm,EF = 4 cm,BG = 4.8 cm. 求 EH 的长.
A
G
B
C
D
E
F
H
解:∵ △ABC∽△DEF,
∴ ,
∴ ,
解得 EH = 3.2 ( cm ).
答:EH 的长为 3.2 cm.
课堂小结
相似三角形的性质
相似三角形对应高的比等于相似比
相似三角形对应角平分线的比等于相似比
相似三角形对应中线的比等于相似比
一块直角三角形木板的一条直角边 AB 长为 1.5 m,面积为 1.5 m2,要把它加工成一个面积尽可能大的正方形桌面,请同学们设计加工方法.
A
B
C
实践与拓展
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
